三角形相似的判定(二)[下学期]
图片预览


文档简介
课件15张PPT。§4.7三角形相似的判定(二)
执教者:陈万勇§4.7三角形相似的判定(二)
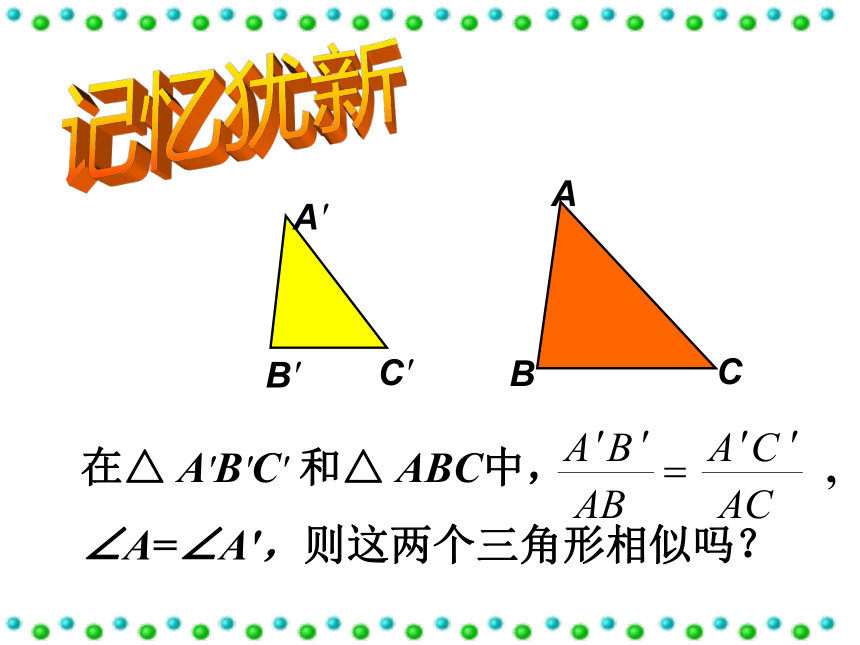
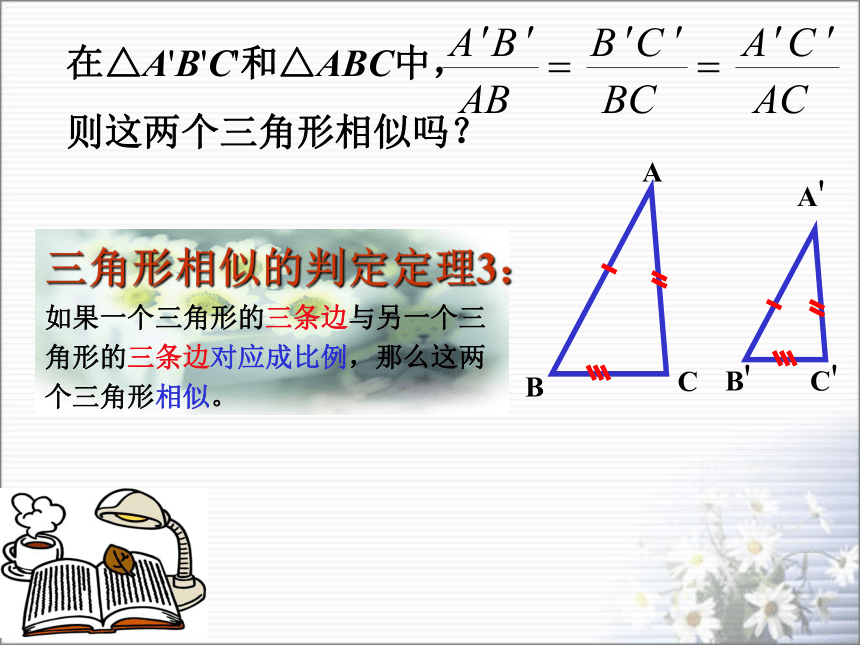
执教者:陈万勇C'B'A'在△ A'B'C' 和△ ABC中, ,
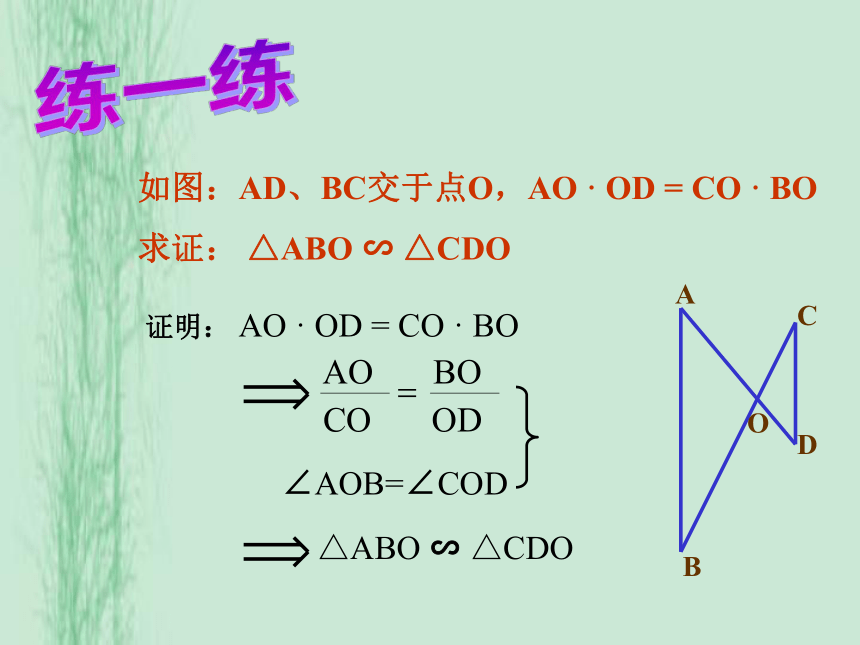
∠A=∠A',则这两个三角形相似吗?记忆犹新练一练如图:AD、BC交于点O,AO · OD = CO · BO
求证: △ABO ∽ △CDO证明: AO · OD = CO · BO
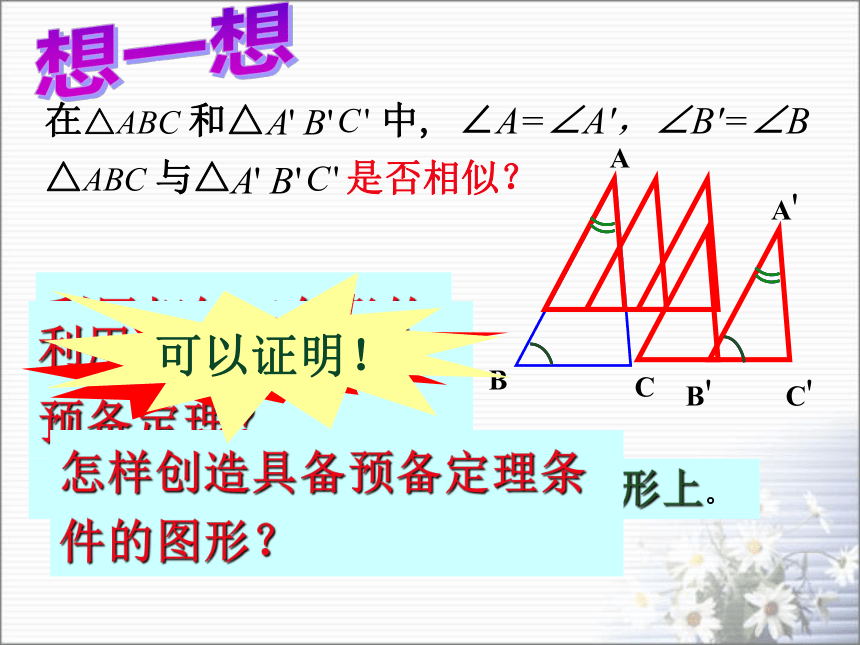
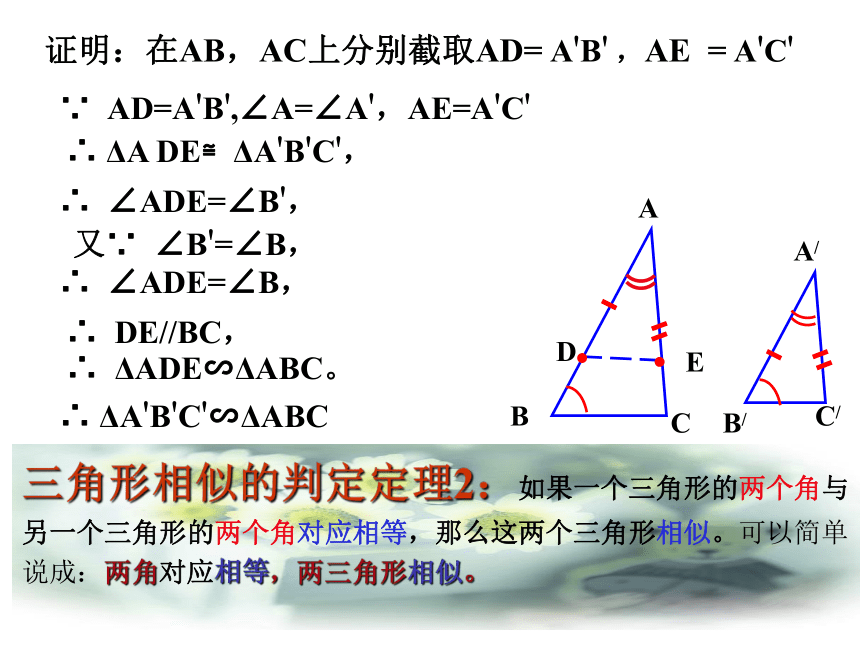
∠AOB=∠COD在△ABC 和△ 中, ∠A=∠A',∠B'=∠B△ABC 与△ 把小的三角形移动到大的三角形上。是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!想一想ABCA/ C/ B/ 三角形相似的判定定理2:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'CC'在△A'B'C'和△ABC中,
则这两个三角形相似吗?三角形相似的判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。梳 理 概 括 今天我们学习了三角形相似的判定定理2,判定定理3,那么在判定三角形相似时,同学们可以根据具体条件,来选择合适的判定方法。 依据下列各组条件,判定△ABC和 △A’B’C’ 是否相似,并说明理由:(1)∠A=35°, AB=12cm, AC=15cm
∠A’=35° A’B’=12cm, A’C’=15cm(2) ∠A=105°, ∠B=15°
∠A’=105°, ∠B’=60°(3) AB=12cm, BC=15cm, AC=24cm
A’B’=20cm,B’C’=25cm,A’C’=40cm应用新知△ABC ∽△A'B'C' △ABC ∽△A'C'B' △ABC ∽△A'B'C' (判定定理1)(判定定理2)(判定定理3)共同研究例1:如图D是△ABC的边AC上一点,DE∥BC交AB于点E,DF∥AB交BC于F,
求证:△AED∽△DFC.
巩固练习如图,AD是△ABC的角平分线,E是AC上一点,且∠AED=∠ADB
求证:AD是AB,AC的比例中项.
证明: AD是△ABC的角平分线
∠AED=∠ADB合作交流例2:如图, 在△ABC内任取一点O,分别连结OA,OB,OC,并延长到点A', B', C' ,使
连结A'B' , B'C' , C'A'
求证:△A'B'C' ∽△ABC
∠A'OB=∠AOB证明:同理,得A'B'C'OCAB回首一眸 如图, 在边长为1的正方形网格上有P,A,B,C四点
求证:△PAB ∽△PCA
提示:用两边对应成比例,夹角相等或三边对应成比例来证动脑筋任意作一个三角形,用类似于例2的方法,把1:2的比例(即相似比)缩小。祝同学们
学习进步再见
执教者:陈万勇§4.7三角形相似的判定(二)
执教者:陈万勇C'B'A'在△ A'B'C' 和△ ABC中, ,
∠A=∠A',则这两个三角形相似吗?记忆犹新练一练如图:AD、BC交于点O,AO · OD = CO · BO
求证: △ABO ∽ △CDO证明: AO · OD = CO · BO
∠AOB=∠COD在△ABC 和△ 中, ∠A=∠A',∠B'=∠B△ABC 与△ 把小的三角形移动到大的三角形上。是否相似?利用相似三角形的定义?利用相似三角形的预备定理?怎样创造具备预备定理条件的图形? 条件不够可以证明!想一想ABCA/ C/ B/ 三角形相似的判定定理2:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A'B',∠A=∠A',AE=A'C'∴ ΔA DE≌ΔA'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA'B'C'∽ΔABC证明:在AB,AC上分别截取AD= A'B' ,AE = A'C'CC'在△A'B'C'和△ABC中,
则这两个三角形相似吗?三角形相似的判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。梳 理 概 括 今天我们学习了三角形相似的判定定理2,判定定理3,那么在判定三角形相似时,同学们可以根据具体条件,来选择合适的判定方法。 依据下列各组条件,判定△ABC和 △A’B’C’ 是否相似,并说明理由:(1)∠A=35°, AB=12cm, AC=15cm
∠A’=35° A’B’=12cm, A’C’=15cm(2) ∠A=105°, ∠B=15°
∠A’=105°, ∠B’=60°(3) AB=12cm, BC=15cm, AC=24cm
A’B’=20cm,B’C’=25cm,A’C’=40cm应用新知△ABC ∽△A'B'C' △ABC ∽△A'C'B' △ABC ∽△A'B'C' (判定定理1)(判定定理2)(判定定理3)共同研究例1:如图D是△ABC的边AC上一点,DE∥BC交AB于点E,DF∥AB交BC于F,
求证:△AED∽△DFC.
巩固练习如图,AD是△ABC的角平分线,E是AC上一点,且∠AED=∠ADB
求证:AD是AB,AC的比例中项.
证明: AD是△ABC的角平分线
∠AED=∠ADB合作交流例2:如图, 在△ABC内任取一点O,分别连结OA,OB,OC,并延长到点A', B', C' ,使
连结A'B' , B'C' , C'A'
求证:△A'B'C' ∽△ABC
∠A'OB=∠AOB证明:同理,得A'B'C'OCAB回首一眸 如图, 在边长为1的正方形网格上有P,A,B,C四点
求证:△PAB ∽△PCA
提示:用两边对应成比例,夹角相等或三边对应成比例来证动脑筋任意作一个三角形,用类似于例2的方法,把1:2的比例(即相似比)缩小。祝同学们
学习进步再见
