抽象函数初步

课件10张PPT。抽象函数：没有给出具体解析式的函数在高考中，常以抽象函数为载体，考查函数的定义域，值域，单调性，奇偶性，周期性及图象问题。
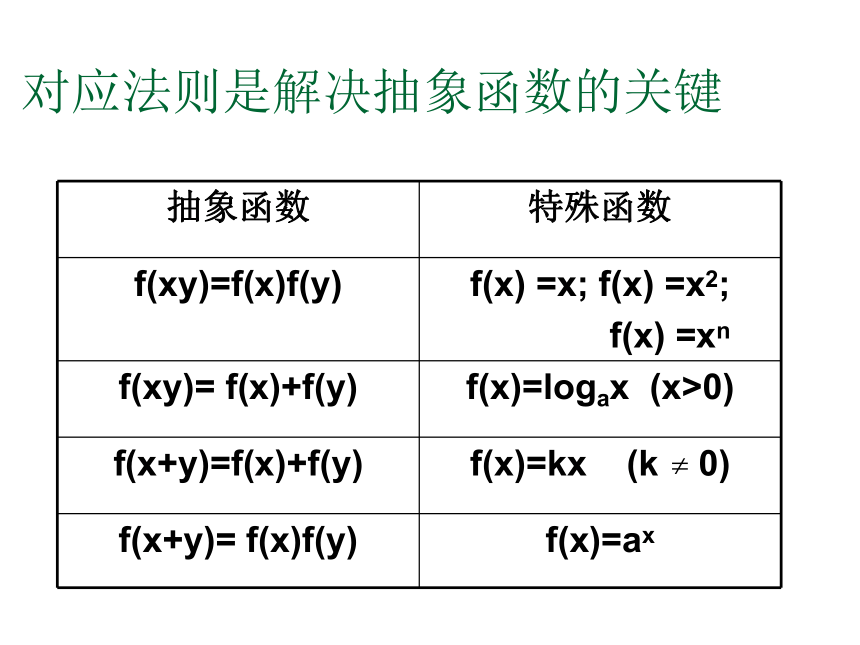
抽象函数初步对应法则是解决抽象函数的关键例1、函数f(x)的定义域为 ，对 任意正实数x,y都有f(xy)= f(x)+f(y)
且f(4)=2 ，则 ________变式：函数f(x)是定义域为(0,+∞)的增函数，且对定义域内任意实数x,y都有f(xy)= f(x)+f(y) ，若f(3)=1，且f(a)>f(a-1)+2，求a的取值范围.f(xy)= f(x)+f(y)练习：设函数f(x)（ ） 为奇函数，
，f(x+2)=f(x)+f(2) ，则f(5)=——变式：函数f(x)的定义域为R，对 任意实数x,y都有f(x+y)= f(x)+f(y) .
(1)判断函数f(x)的奇偶性;
(2)若当x<0时，f(x)>0,则函数f(x)在
[a,b]上的最小值为______________.f(x+y)= f(x)+f(y) 题后反思
题型：
方法：
填空题，选择题1、特殊法
（化抽象函数为具体函数）3、直接法（按对应法则来处理）2、赋值法（取特殊值）例2、函数f(x)是定义在R上的奇函数，且
Y= f(x)的 图象关于 对称，则
————练习：函数f(x)是定义在R上的以3为周期的奇函数，且f(2)=0，则f(5)=__,f(-2)=__, f(1)=__, f(0)=__, f(3)=__ ,f(1.5)=__,f(4.5)=__.变式：函数f(x)是定义在R上的以3为周期的奇函数，且f(2)=0，则方程f(x)=0在区间（0，6）内的解的 个数的最小值为
A 4 B 5 C 6 D 7 题后反思
考查的知识点：

方法：
函数的周期性，
奇偶性，对称性图象法（化无形为有形）例4、 已知f (x)是定义在R上的不恒为零的函数，且对于任意的 ,都 满足f(ab)= af(b)+bf(a)
（1）求f (0), f (1)的值；
（2）判断f (x)的奇偶性,并证明你的结论；
课堂小结：1、考查抽象函数的哪些性质？2、基本方法有哪些？