函数的单调性

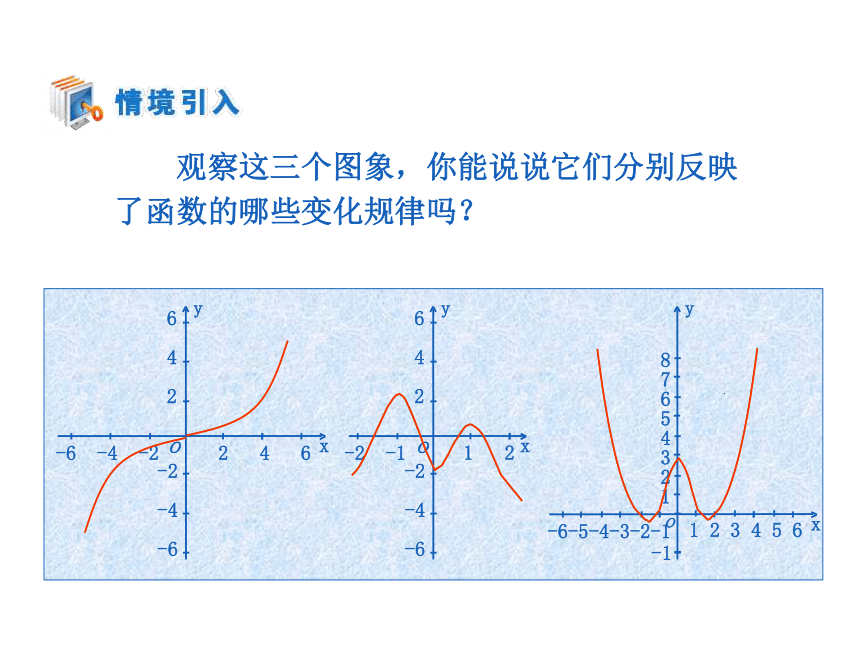
课件22张PPT。　　观察这三个图象，你能说说它们分别反映
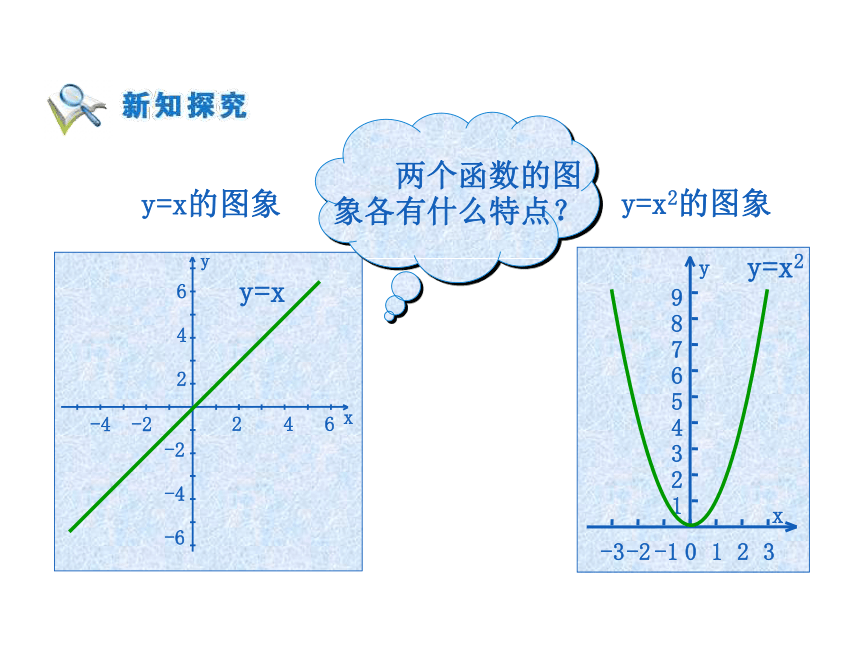
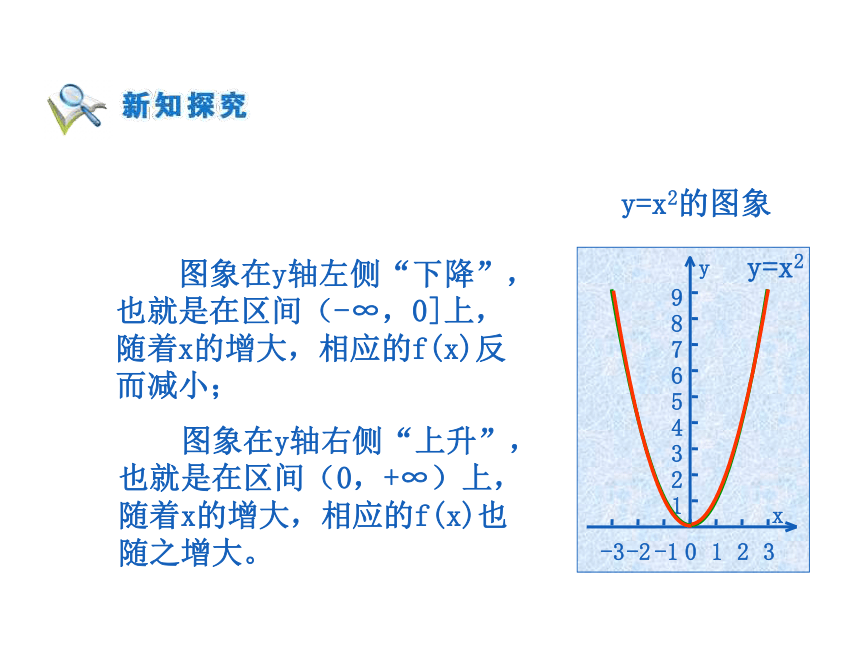
了函数的哪些变化规律吗？ y=x2的图象 　　图象在y轴左侧“下降”，
也就是在区间（-∞，0]上，
随着x的增大，相应的f(x)反
而减小； 　　图象在y轴右侧“上升”，
也就是在区间（0，+∞）上，
随着x的增大，相应的f(x)也
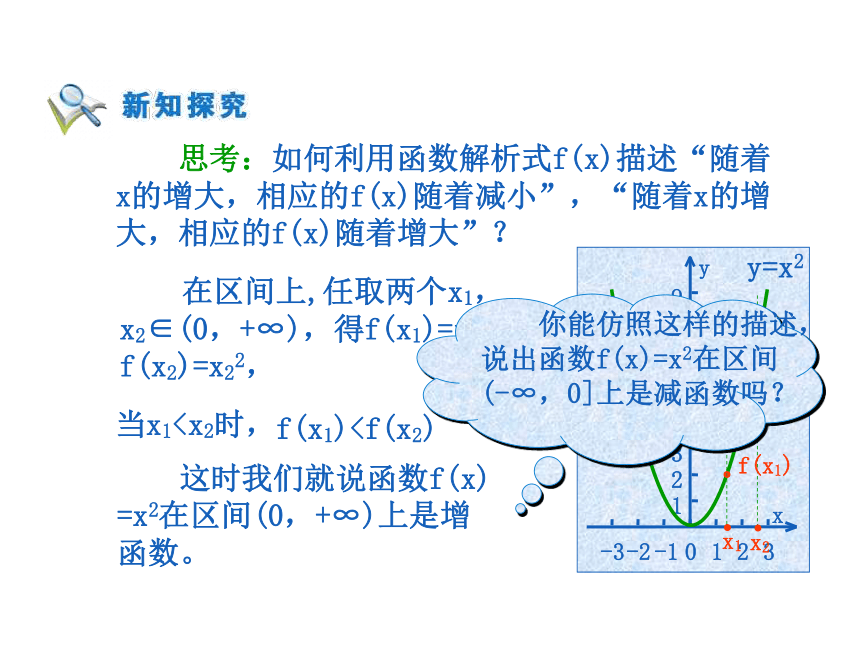
随之增大。　　思考：如何利用函数解析式f(x)描述“随着
x的增大，相应的f(x)随着减小”，“随着x的增
大，相应的f(x)随着增大”？　　在区间上,任取两个x1，
x2∈(0，+∞)，得f(x1)=x12，
f(x2)=x22，..x1x2f(x1)f(x2)..　　这时我们就说函数f(x)
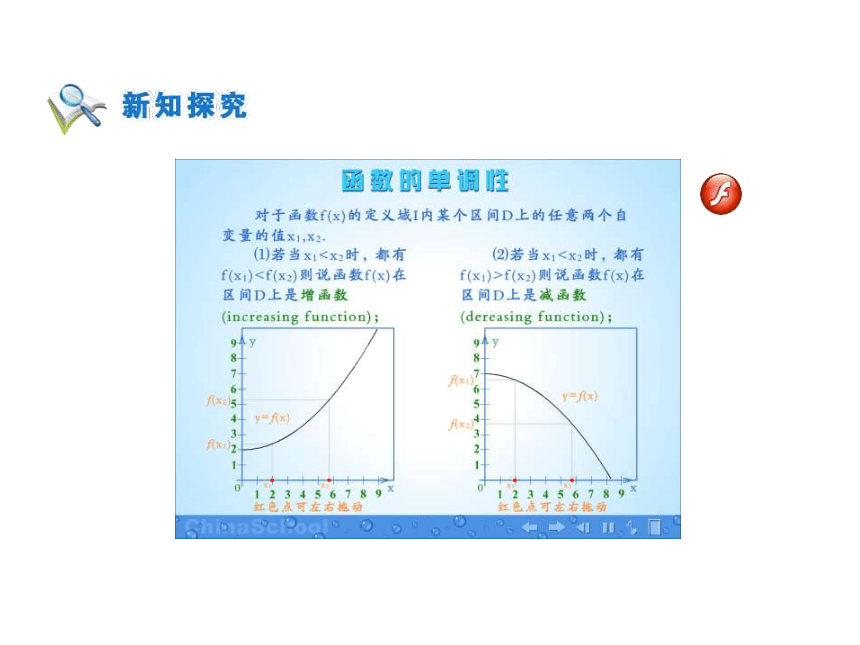
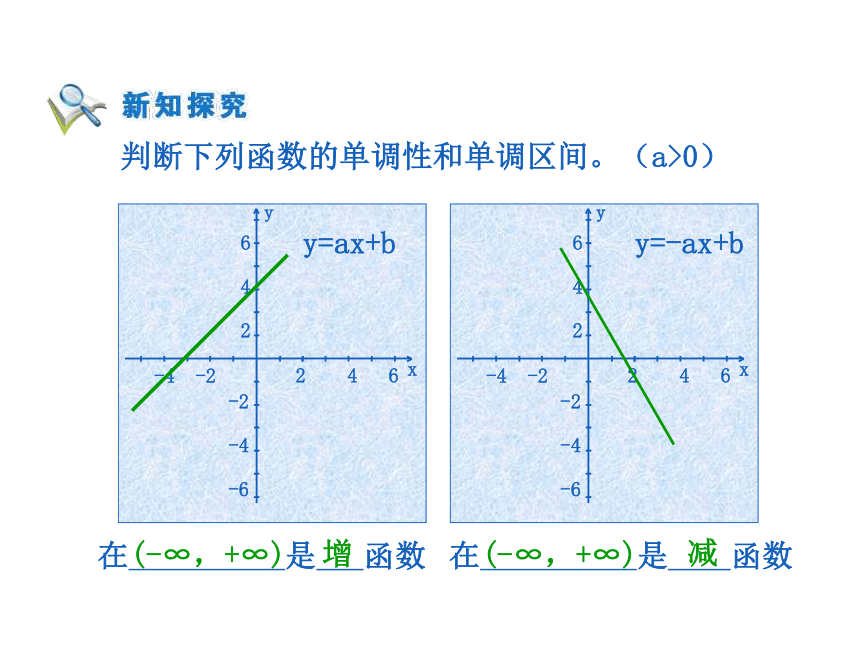
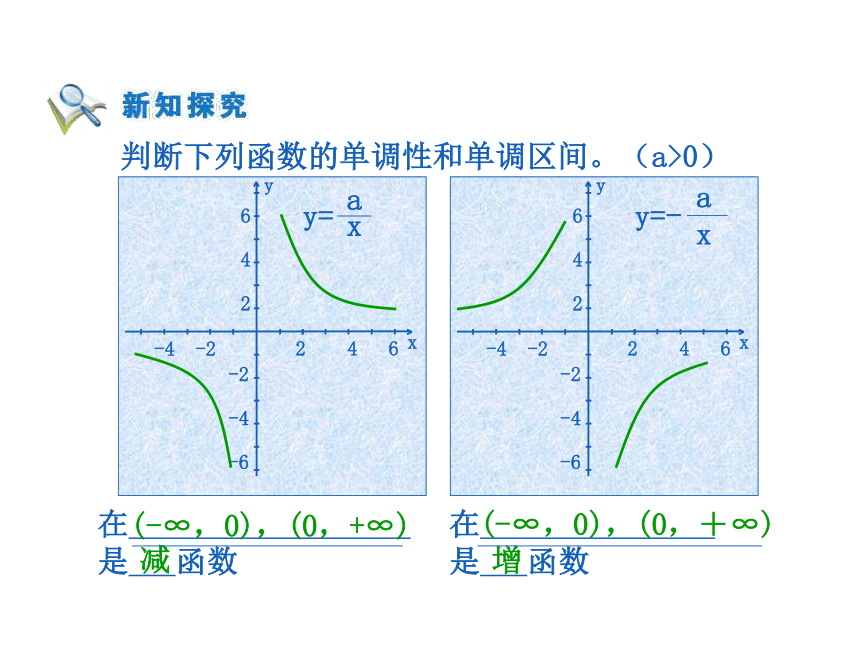
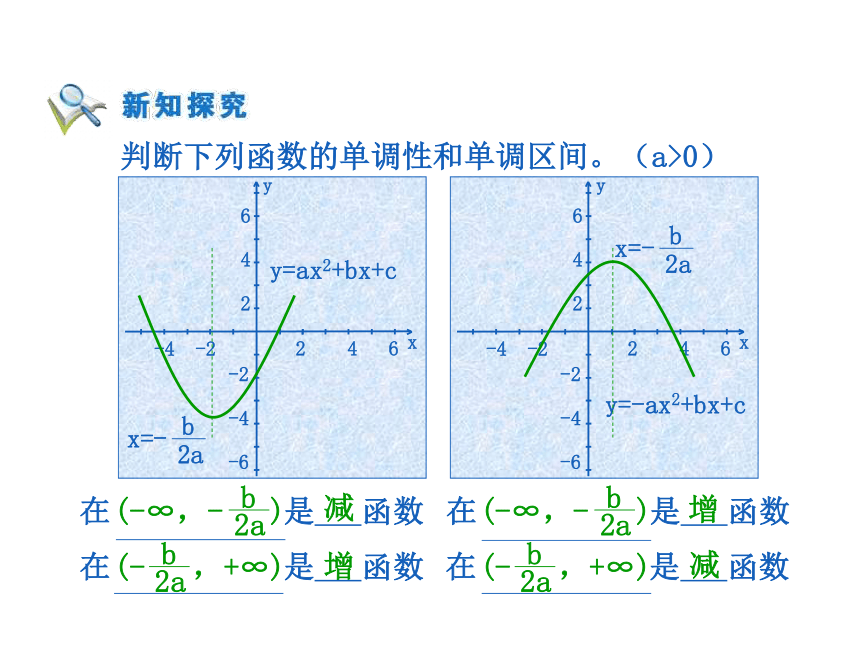
=x2在区间(0，+∞)上是增函数。当x10）(-∞，+∞)(-∞，+∞)增减　　判断下列函数的单调性和单调区间。（a>0）增减(-∞，0)，(0，+∞)(-∞，0)，(0，＋∞) 　　判断下列函数的单调性和单调区间。（a>0）增减减增　　图象是定义在[-5，5]上的函数f(x)，根据
图象说出函数的单调区间，以及在每一个区间
上，它是增函数还是减函数。解：由图象可以看出：函数
y=f(x)的单调区间有[-5，
-2)，[-2，1)，[1，3），
[3，5]。　　y=f(x)在区间[-5，-2)，
[1，3)是减函数在区间[-2，
1)，[3，5]是增函数。　　图象是定义在[-5，5]上的函数f(x)，根据
图象说出函数的单调区间，以及在每一个区间
上，它是增函数还是减函数。思考：如果把在区间[-5，-2)，[1，3)是减函数
写成{x|-5（0，+∞）上的任意两个实数，且V10由V10 由k>0，于是P(V1)-P(V2)>0 即P(V1)>P(V2)也就是说，当体积V减小时，压强P将增大。 　　整个上午(8:00-12:00)天气越来越暖，中午
时分(12:00-13:00)一场暴风雨使天气骤然凉爽
了许多。暴风雨过后，天气转暖，直到太阳落山
(18:00)才又开始转凉，画出这一天8:00-20:00
期间气温作为时间函数的一个可能的图象，并说
出所画图象的单调区间。增区间为:
　　[8，12]，[13，18]减区间为:
　　[12，13]，[18，20]　　根据图象说出函数的单调区间，以及在每
一单调区间上，函数是增函数还是减函数。在　　　 上是减函数, 在　　　 上是增函数;
在　　　 上是减函数, 在　　　 上是增函数。 [-1，0][0，2][4，5][2，4]　　证明函数f(x)=2x-3在R上是增函数。证明：根据单调性的定义，任取x1，x2∈R，
且x1 =2(x1- x2)因为x1(1)在区间(-∞，1]上是单调递增函数，
(2)在区间[1，+∞)上是单调递减函数。　　f(x1)-f(x2)=-(x1-x2)[x1+x2-2]　因为x10 即f(x1)>f(x2) 　　所以函数f(x)=-x2+2x-3在区间[1，+∞)上
是减函数。所以x1- x2<0 所以x1+x2>2，即x1+x2-2>0 已知函数f(x)的定义域为R，对任意实数m、n均有f(m+n)=f(m)+f(n)-1，且f(0.5)=2，又当x>-0.5时，有f(x)>0。
(1) 求f(-0.5)的值；
　　(2) 求证：f(x)是单调递增函数。解：(1)
令m=n=0，则f(0)=f(0)+f(0)-1，所以f(0)=1
又f(0.5-0.5)=f[0.5+(-0.5)]=f(0.5)+f(-0.5)-1
所以f(0)=2+f(-0.5)-1，
f(-0.5)=f(0)-1=0. 已知函数f(x)的定义域为R，对任意实数m、n均有f(m+n)=f(m)+f(n)-1，且f(0.5)=2，又当x>-0.5时，有f(x)>0。
(1) 求f(-0.5)的值；
　　(2) 求证：f(x)是单调递增函数。解：(2)
　　设x10，x2-x1-0.5>-0.5.
又x>-0.5时又f(x)>0，所以ｆ(x2-x1-0.5)>0。
又f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)
=f(x2-x1)-f(x1)-1-f(x1)=f(x2-x1)-1
=f(x2-x1)+f(-0.5)-1=f(x2-x1-0.5)>0，
所以f(x2)>f(x1)，所以f(x)在R上为增函数。