1.函数单调性的应用
图片预览






文档简介
课件14张PPT。函数单调性的应用教学目的
重点难点
教学过程
退 出
教学目的使学生通过对知识的运用加深对知识的理解与掌握。
在问题解决的过程中渗透数形结合的思想方法和运动、变化的观点。
引导学生挖掘知识的作用,提高运用知识分析问题和解决问题的能力。
返回重点难点二次函数在闭区间上的最值的探求
返回
教学过程 函数单调性的概念
单调性的应用举例
小 结 函数单调性的概念单调函数的图象特征在闭区间[a,b]上单调递增的函数其图象变化的趋势;
在闭区间[a,b]上单调递减的函数其图象变化的趋势;
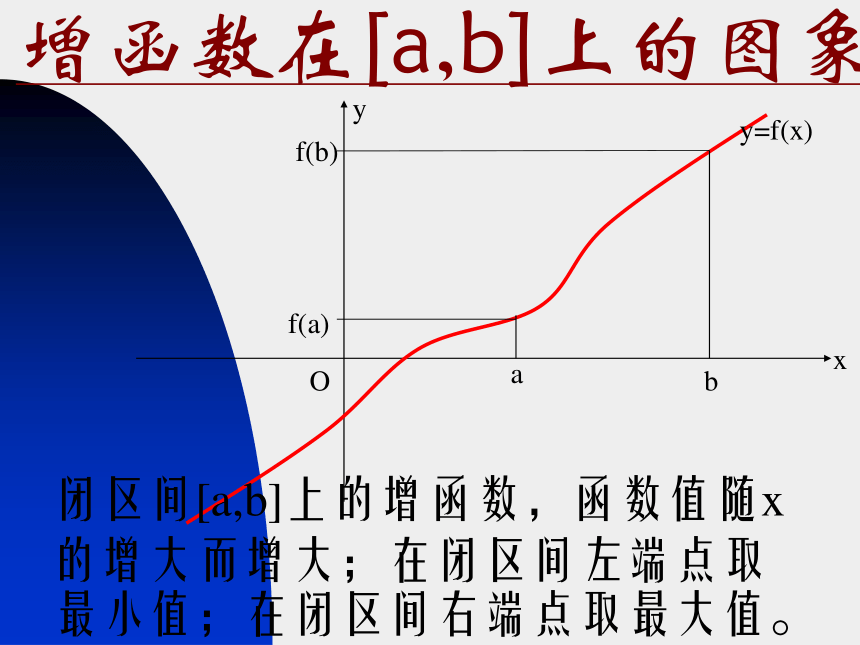
结合图象,请指出函数值变化的趋势,从中能得到一些什么结论?增函数在[a,b]上的图象xyOab y=f(x) f(a) f(b)闭区间[a,b]上的增函数,函数值随x的增大而增大;在闭区间左端点取最小值;在闭区间右端点取最大值。减函数在[a,b]上的图象Oab f(a) f(b)yx y=f(x)闭区间[a,b]上的减函数,函数值随x的增大而减小;在闭区间左端点取最大值;在闭区间右端点取最小值。闭区间上的单调函数的性质若函数y=f(x)在闭区间[a,b]上单调递增,则函数在此区间上的最小值为f(a),最大值为f(b)。
若函数y=f(x)在闭区间[a,b]上单调递减,则函数在此区间上的最小值为f(b),最大值为f(a)。
若函数y=f(x)在闭区间[a,b]上有增有减,则函数在此区间上仍有最小值和最大值,最值可能在区间内取得,也可能在端点处取得。应用举例
例题1,
例题2
应用举例例1,求下列函数的最值:
应用举例例2,求下列函数的最值:小 结若函数y=f(x)在闭区间[a,b]上单调递增,则函数在此区间上的最小值为f(a),最大值为f(b)。
若函数y=f(x)在闭区间[a,b]上单调递减,则函数在此区间上的最小值为f(b),最大值为f(a)。
若函数y=f(x)在闭区间[a,b]上有增有减,则函数在此区间上仍有最小值和最大值,最值可能在区间内取得,也可能在端点处取得。再 见!
重点难点
教学过程
退 出
教学目的使学生通过对知识的运用加深对知识的理解与掌握。
在问题解决的过程中渗透数形结合的思想方法和运动、变化的观点。
引导学生挖掘知识的作用,提高运用知识分析问题和解决问题的能力。
返回重点难点二次函数在闭区间上的最值的探求
返回
教学过程 函数单调性的概念
单调性的应用举例
小 结 函数单调性的概念单调函数的图象特征在闭区间[a,b]上单调递增的函数其图象变化的趋势;
在闭区间[a,b]上单调递减的函数其图象变化的趋势;
结合图象,请指出函数值变化的趋势,从中能得到一些什么结论?增函数在[a,b]上的图象xyOab y=f(x) f(a) f(b)闭区间[a,b]上的增函数,函数值随x的增大而增大;在闭区间左端点取最小值;在闭区间右端点取最大值。减函数在[a,b]上的图象Oab f(a) f(b)yx y=f(x)闭区间[a,b]上的减函数,函数值随x的增大而减小;在闭区间左端点取最大值;在闭区间右端点取最小值。闭区间上的单调函数的性质若函数y=f(x)在闭区间[a,b]上单调递增,则函数在此区间上的最小值为f(a),最大值为f(b)。
若函数y=f(x)在闭区间[a,b]上单调递减,则函数在此区间上的最小值为f(b),最大值为f(a)。
若函数y=f(x)在闭区间[a,b]上有增有减,则函数在此区间上仍有最小值和最大值,最值可能在区间内取得,也可能在端点处取得。应用举例
例题1,
例题2
应用举例例1,求下列函数的最值:
应用举例例2,求下列函数的最值:小 结若函数y=f(x)在闭区间[a,b]上单调递增,则函数在此区间上的最小值为f(a),最大值为f(b)。
若函数y=f(x)在闭区间[a,b]上单调递减,则函数在此区间上的最小值为f(b),最大值为f(a)。
若函数y=f(x)在闭区间[a,b]上有增有减,则函数在此区间上仍有最小值和最大值,最值可能在区间内取得,也可能在端点处取得。再 见!
