函数的单调性
图片预览




文档简介
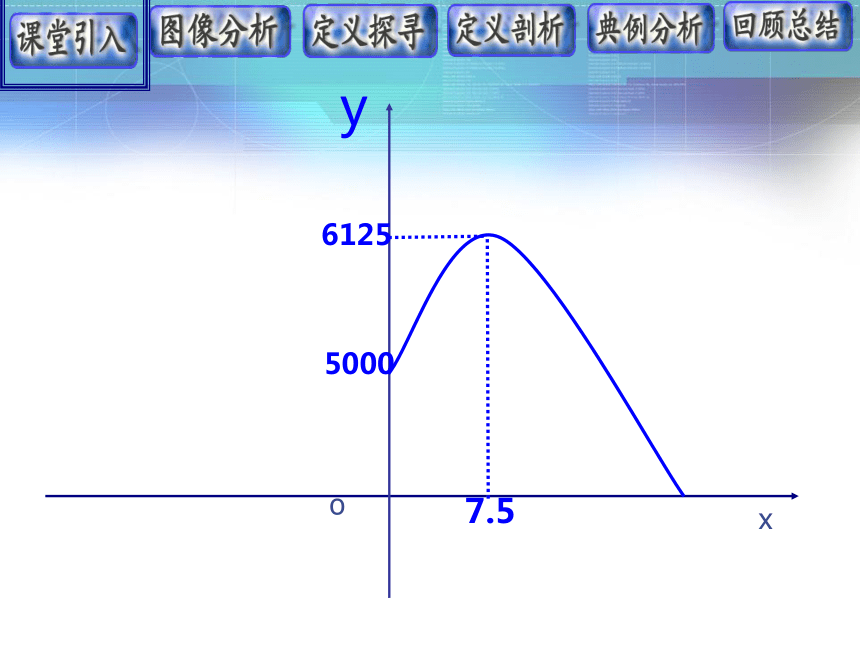
课件14张PPT。函数的单调性某超市将进货单价为40元的“首乌”洗发露,按50元一瓶出售时,每天能卖出500瓶,根据市场分析,单价每提高1元,其每天销售量将减低20瓶,问应怎样制定洗发露的售价,每天才能获得最大利润?问题大家知道,市场中价格低则销量大,价格高则单个利润大,最终利润是由两者共同决定的,那么随着价格的变化,利润是如何变化的呢?分析:
当价格提高 元后的利润是:
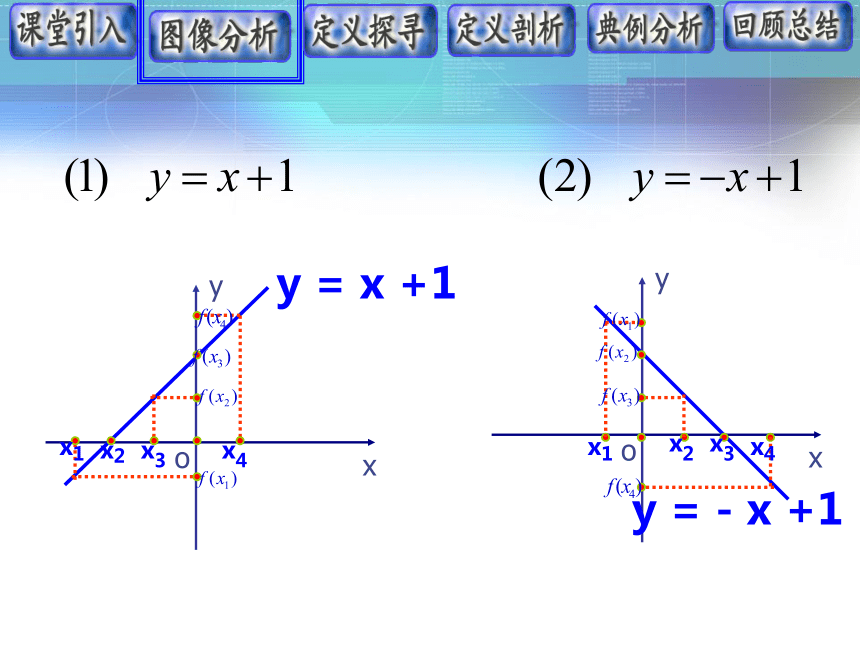
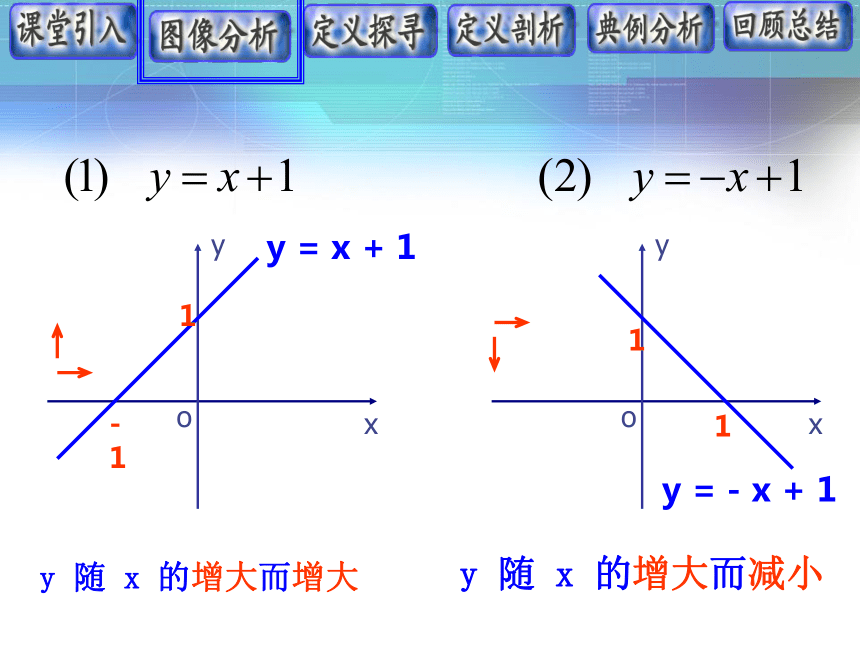
y7.561255000y = - x +1xxxxxxxx12341234y = x + 1y = - x + 1y 随 x 的增大而增大y 随 x 的增大而减小我们可以观察上述函数中,图像从左至右,分别是上升下降的,函数图象的“上升”“下降”反映了函数的一个基本性质——单调性,那么如何描述函数的上升下降呢?增(减)函数定义: 一般地,函数 定义域I内某个区间D上任意两个自变量 、 ,当 时,都有
称函数 为区间D上的增函数,区间D称为单调增区间。
<<一般地,函数 定义域I内某个区间D上任意两个自变量 、 ,当 时,都有 称函数 为区间D上的减函数,区间D称为单调减区间。<<1.函数的单调性是对某个区间而言的, 它是一个局部概念。
2.函数单调性比较的是区间中任意两个点的值,具有任意性。y = x2[0,+∞):y 随 x 的增大而增大,即单调增区间(-∞,0]: y 随 x 的增大而减小,即单调减区间判断二次函数 ,在区间 [-1,2], [-1,0] , [0,2]上的单调性,并指出其单调区间。例1:解:[-1,2] 不具单调性
[-1,0] 单调递减
[0 ,2] 单调递增-1 2 4 1 增区间(-2, 2] ,[3,5)
减区间 [-5,-2),[2,3]
单调区间(-2, 2] ,[3,5),[-5,-2),[2,3] 例2:说出下面函数的单调区间。解:例3:物理学中的玻意尔定律 (k为正常数)告诉我们,对于一定量的气体,当体积V减小时,压强p将增大,试用函数单调性证明之。按题意,只要证明函数 在区间(0,+∞)为减函数即可。解:根据函数的定义域,设 是定义域(0,+ ∞)上的任意两个实数,且 < ,则
由 (0,+∞) 得 > ,
由 < 得 > ,
又k>0于是 > ,即 >
所以,函数 v∈ (0,+∞) 是减函数,也就是
说,当体积V减小时,压强p将增大。
分析:例3:画出反比例函数 的图像。
(1)该函数的定义域I是什么?
(2)在定义域内单调性是怎样的?
解:(1)定义域是(-∞,0)∪(0,+ ∞)(2)单调区间是(-∞,0)和(0,+ ∞) 还是(-∞,0)∪(0,+ ∞)x1x2y1y2x2x1y1y2
当价格提高 元后的利润是:
y7.561255000y = - x +1xxxxxxxx12341234y = x + 1y = - x + 1y 随 x 的增大而增大y 随 x 的增大而减小我们可以观察上述函数中,图像从左至右,分别是上升下降的,函数图象的“上升”“下降”反映了函数的一个基本性质——单调性,那么如何描述函数的上升下降呢?增(减)函数定义: 一般地,函数 定义域I内某个区间D上任意两个自变量 、 ,当 时,都有
称函数 为区间D上的增函数,区间D称为单调增区间。
<<一般地,函数 定义域I内某个区间D上任意两个自变量 、 ,当 时,都有 称函数 为区间D上的减函数,区间D称为单调减区间。<<1.函数的单调性是对某个区间而言的, 它是一个局部概念。
2.函数单调性比较的是区间中任意两个点的值,具有任意性。y = x2[0,+∞):y 随 x 的增大而增大,即单调增区间(-∞,0]: y 随 x 的增大而减小,即单调减区间判断二次函数 ,在区间 [-1,2], [-1,0] , [0,2]上的单调性,并指出其单调区间。例1:解:[-1,2] 不具单调性
[-1,0] 单调递减
[0 ,2] 单调递增-1 2 4 1 增区间(-2, 2] ,[3,5)
减区间 [-5,-2),[2,3]
单调区间(-2, 2] ,[3,5),[-5,-2),[2,3] 例2:说出下面函数的单调区间。解:例3:物理学中的玻意尔定律 (k为正常数)告诉我们,对于一定量的气体,当体积V减小时,压强p将增大,试用函数单调性证明之。按题意,只要证明函数 在区间(0,+∞)为减函数即可。解:根据函数的定义域,设 是定义域(0,+ ∞)上的任意两个实数,且 < ,则
由 (0,+∞) 得 > ,
由 < 得 > ,
又k>0于是 > ,即 >
所以,函数 v∈ (0,+∞) 是减函数,也就是
说,当体积V减小时,压强p将增大。
分析:例3:画出反比例函数 的图像。
(1)该函数的定义域I是什么?
(2)在定义域内单调性是怎样的?
解:(1)定义域是(-∞,0)∪(0,+ ∞)(2)单调区间是(-∞,0)和(0,+ ∞) 还是(-∞,0)∪(0,+ ∞)x1x2y1y2x2x1y1y2
