第二章 气体、固体和液体 专题 封闭气体压强的计算-高中物理人教版选择性必修3(共25张PPT)
文档属性
| 名称 | 第二章 气体、固体和液体 专题 封闭气体压强的计算-高中物理人教版选择性必修3(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-22 13:51:19 | ||
图片预览







文档简介
(共25张PPT)
第二章 气体、固体和液体
专题:封闭气体压强的计算
2
熟练掌握非平衡态下封闭气体压强的计算方法。
1
熟练掌握平衡态下封闭气体压强的计算方法。
重难点
难点
平衡态下活塞、汽缸封闭气体压强的计算
如图所示,汽缸置于水平地面上,活塞质量为m,横截面积为S,汽缸与活塞之间无摩擦,设大气压强为p0,重力加速度为g,试求封闭气体的压强。
答案 以活塞为研究对象,受力分析如图所示,由平衡条件得mg+p0S=pS,则p=p0+ 。
观察与思考
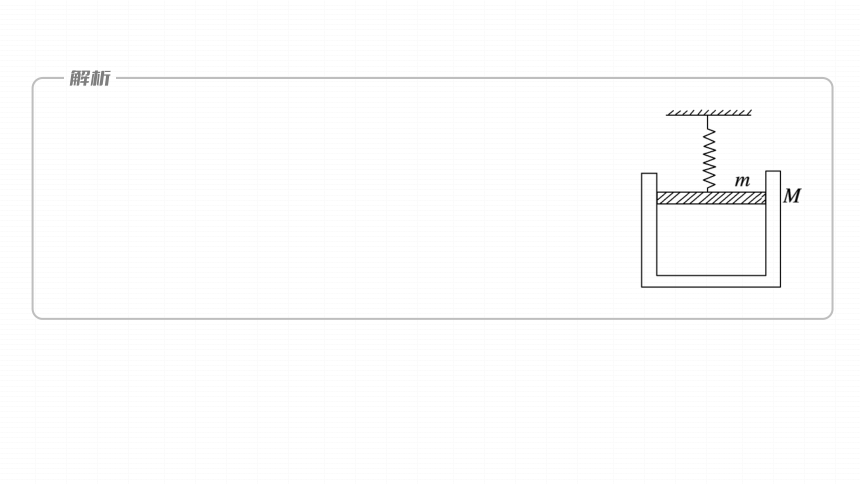
1.如图所示,活塞的质量为m,缸套的质量为M,通过弹簧静止吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞横截面积为S,大气压强为p0,重力加速度为g,则封闭气体的压强p为
√
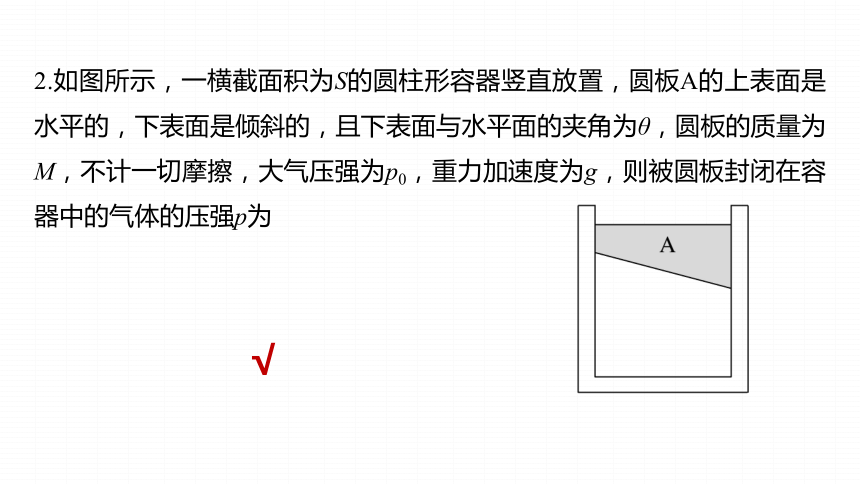
2.如图所示,一横截面积为S的圆柱形容器竖直放置,圆板A的上表面是水平的,下表面是倾斜的,且下表面与水平面的夹角为θ,圆板的质量为M,不计一切摩擦,大气压强为p0,重力加速度为g,则被圆板封闭在容器中的气体的压强p为
√
以圆板为研究对象,对圆板受力分析,如图所示,竖直方向受力平衡,则
解决平衡态下活塞(或汽缸)封闭气体压强的基本思路:
(1)对活塞(或汽缸)进行受力分析,画出受力示意图。
(2)列出活塞(或汽缸)的平衡方程,求出未知量。
注意:不要忘记汽缸底部和活塞外面的大气压强。
总结提升
平衡态下液体封闭气体压强的计算
如图所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,其他条件已标于图上,试求封闭气体A的压强。
观察与思考
1.取等压面法
同种液体在同一深度向各个方向的压强相等,在连通器中,灵活选取等压面,利用液面压强相等求解气体压强。如图甲所示,同一液面C、D两处压强相等,故pA=p0+ph。
2.参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强。
例如:图甲中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知(pA+ρgh0)S=(p0+ρgh+ρgh0)S,即pA=p0+ph。
3.力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强。
例如:甲图中取高为h的液柱为研究对象,对其受力分析,受力示意图如图乙所示,
则pAS=p0S+mg=p0S+ρShg
即pA=p0+ph。
注意:①在考虑与气体接触的液柱所产生的附加压强p=ρgh时,应特别注意h是表示液面间竖直高度,不一定是液柱长度。
②求由液体封闭的气体压强,一般选择最低液面列平衡方程。
3.求图中被封闭气体A的压强。其中(1)、(2)、(3)图中的玻璃管内都装有
水银,(4)图中的小玻璃管浸没在水中。大气压强p0=76 cmHg=1.01×
105 Pa。(g=10 m/s2,ρ水=1×103 kg/m3)
答案 (1)66 cmHg (2)71 cmHg (3)81 cmHg (4)1.13×105 Pa
(1)pA=p0-ph=76 cmHg-10 cmHg=66 cmHg。
(2)pA=p0-ph=76 cmHg-10sin 30° cmHg=71 cmHg。
(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHg,
pA=pB-ph1=86 cmHg-5 cmHg=81 cmHg。
(4)pA=p0+ρ水gh=1.01×105 Pa+1×103×10×1.2 Pa=1.13×105 Pa。
4.(2022·黑龙江哈师大附中高二期末)如图所示,竖直静止放置的U形管,左端开口,右端封闭,管内a、b两段水银柱将A、B两段空气柱封闭在管内。已知水银柱a长为h1,压强为ph1水银柱b两液面的高度差为h2,该段的压强为ph2,大气压强为p0,空气柱A的压强为pA。则空气柱B的压强pB可表示为
A.pB=p0-ph1
B.pB=pA+ph2
C.pB=p0-pA
D.pB=p0-ph1-ph2
√
由题图可知pB+ph2=pA,可得pB=pA-ph2;又pA+ph1=p0,联立可得pB=p0-ph1-ph2
故D正确,A、B、C错误。
容器加速运动时封闭气体压强的计算
如图所示,玻璃管开口向上,竖直静止放置,外界大气压强为p0,液体密度为ρ,液柱高度为h,重力加速度为g,若将上述玻璃管由静止自由释放,求下落过程中封闭气体的压强。
观察与思考
答案 下落过程中对液柱受力分析如图所示
由牛顿第二定律得
p0S+mg-pS=ma ①
a=g ②
联立①②解得p=p0。
5.如图所示,光滑水平面上放有一质量为M的汽缸,汽缸内放有一质量为m的可在汽缸内无摩擦滑动的活塞,活塞横截面积为S。现用水平恒力F向右推汽缸,最后汽缸和活塞达到相对静止状态,求此时缸内封闭气体的压强p。(已知外界大气压强为p0)
选取汽缸和活塞整体为研究对象,汽缸和活塞相对静止时有F=(M+m)a ①
以活塞为研究对象,由牛顿第二定律有
pS-p0S=ma ②
6.有一段12 cm长的水银柱,在均匀玻璃管中封住了一定质量的气体,若将玻璃管口向上放在一个倾角为30°的光滑斜面上,在玻璃管自由下滑过程中稳定后被封闭气体的压强为(设大气压强为p0=76 cmHg)
A.70 cmHg
B.76 cmHg
C.82 cmHg
D.88 cmHg
√
以玻璃管与水银柱整体为研究对象,有Mgsin 30°=Ma,得a= ①,
水银柱相对玻璃管静止,则二者加速度相等,以水银柱为研究对象有mgsin 30°+p0S-pS=ma ②,
将①代入②得p=p0=76 cmHg,选B。
解决非平衡态下封闭气体压强的基本思路:
1.当容器加速运动时,通常选与气体相关联的液柱、汽缸或活塞为研究对象,并对其进行受力分析,然后由牛顿第二定律列方程,求出封闭气体的压强。
2.在对系统进行分析时,可针对具体情况选用整体法或隔离法。
总结提升
第二章 气体、固体和液体
专题:封闭气体压强的计算
2
熟练掌握非平衡态下封闭气体压强的计算方法。
1
熟练掌握平衡态下封闭气体压强的计算方法。
重难点
难点
平衡态下活塞、汽缸封闭气体压强的计算
如图所示,汽缸置于水平地面上,活塞质量为m,横截面积为S,汽缸与活塞之间无摩擦,设大气压强为p0,重力加速度为g,试求封闭气体的压强。
答案 以活塞为研究对象,受力分析如图所示,由平衡条件得mg+p0S=pS,则p=p0+ 。
观察与思考
1.如图所示,活塞的质量为m,缸套的质量为M,通过弹簧静止吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞横截面积为S,大气压强为p0,重力加速度为g,则封闭气体的压强p为
√
2.如图所示,一横截面积为S的圆柱形容器竖直放置,圆板A的上表面是水平的,下表面是倾斜的,且下表面与水平面的夹角为θ,圆板的质量为M,不计一切摩擦,大气压强为p0,重力加速度为g,则被圆板封闭在容器中的气体的压强p为
√
以圆板为研究对象,对圆板受力分析,如图所示,竖直方向受力平衡,则
解决平衡态下活塞(或汽缸)封闭气体压强的基本思路:
(1)对活塞(或汽缸)进行受力分析,画出受力示意图。
(2)列出活塞(或汽缸)的平衡方程,求出未知量。
注意:不要忘记汽缸底部和活塞外面的大气压强。
总结提升
平衡态下液体封闭气体压强的计算
如图所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,其他条件已标于图上,试求封闭气体A的压强。
观察与思考
1.取等压面法
同种液体在同一深度向各个方向的压强相等,在连通器中,灵活选取等压面,利用液面压强相等求解气体压强。如图甲所示,同一液面C、D两处压强相等,故pA=p0+ph。
2.参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强。
例如:图甲中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知(pA+ρgh0)S=(p0+ρgh+ρgh0)S,即pA=p0+ph。
3.力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强。
例如:甲图中取高为h的液柱为研究对象,对其受力分析,受力示意图如图乙所示,
则pAS=p0S+mg=p0S+ρShg
即pA=p0+ph。
注意:①在考虑与气体接触的液柱所产生的附加压强p=ρgh时,应特别注意h是表示液面间竖直高度,不一定是液柱长度。
②求由液体封闭的气体压强,一般选择最低液面列平衡方程。
3.求图中被封闭气体A的压强。其中(1)、(2)、(3)图中的玻璃管内都装有
水银,(4)图中的小玻璃管浸没在水中。大气压强p0=76 cmHg=1.01×
105 Pa。(g=10 m/s2,ρ水=1×103 kg/m3)
答案 (1)66 cmHg (2)71 cmHg (3)81 cmHg (4)1.13×105 Pa
(1)pA=p0-ph=76 cmHg-10 cmHg=66 cmHg。
(2)pA=p0-ph=76 cmHg-10sin 30° cmHg=71 cmHg。
(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHg,
pA=pB-ph1=86 cmHg-5 cmHg=81 cmHg。
(4)pA=p0+ρ水gh=1.01×105 Pa+1×103×10×1.2 Pa=1.13×105 Pa。
4.(2022·黑龙江哈师大附中高二期末)如图所示,竖直静止放置的U形管,左端开口,右端封闭,管内a、b两段水银柱将A、B两段空气柱封闭在管内。已知水银柱a长为h1,压强为ph1水银柱b两液面的高度差为h2,该段的压强为ph2,大气压强为p0,空气柱A的压强为pA。则空气柱B的压强pB可表示为
A.pB=p0-ph1
B.pB=pA+ph2
C.pB=p0-pA
D.pB=p0-ph1-ph2
√
由题图可知pB+ph2=pA,可得pB=pA-ph2;又pA+ph1=p0,联立可得pB=p0-ph1-ph2
故D正确,A、B、C错误。
容器加速运动时封闭气体压强的计算
如图所示,玻璃管开口向上,竖直静止放置,外界大气压强为p0,液体密度为ρ,液柱高度为h,重力加速度为g,若将上述玻璃管由静止自由释放,求下落过程中封闭气体的压强。
观察与思考
答案 下落过程中对液柱受力分析如图所示
由牛顿第二定律得
p0S+mg-pS=ma ①
a=g ②
联立①②解得p=p0。
5.如图所示,光滑水平面上放有一质量为M的汽缸,汽缸内放有一质量为m的可在汽缸内无摩擦滑动的活塞,活塞横截面积为S。现用水平恒力F向右推汽缸,最后汽缸和活塞达到相对静止状态,求此时缸内封闭气体的压强p。(已知外界大气压强为p0)
选取汽缸和活塞整体为研究对象,汽缸和活塞相对静止时有F=(M+m)a ①
以活塞为研究对象,由牛顿第二定律有
pS-p0S=ma ②
6.有一段12 cm长的水银柱,在均匀玻璃管中封住了一定质量的气体,若将玻璃管口向上放在一个倾角为30°的光滑斜面上,在玻璃管自由下滑过程中稳定后被封闭气体的压强为(设大气压强为p0=76 cmHg)
A.70 cmHg
B.76 cmHg
C.82 cmHg
D.88 cmHg
√
以玻璃管与水银柱整体为研究对象,有Mgsin 30°=Ma,得a= ①,
水银柱相对玻璃管静止,则二者加速度相等,以水银柱为研究对象有mgsin 30°+p0S-pS=ma ②,
将①代入②得p=p0=76 cmHg,选B。
解决非平衡态下封闭气体压强的基本思路:
1.当容器加速运动时,通常选与气体相关联的液柱、汽缸或活塞为研究对象,并对其进行受力分析,然后由牛顿第二定律列方程,求出封闭气体的压强。
2.在对系统进行分析时,可针对具体情况选用整体法或隔离法。
总结提升
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
