【核心素养目标】6.2.2平行四边形的判定 教学设计
文档属性
| 名称 | 【核心素养目标】6.2.2平行四边形的判定 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
6.2.2平行四边形的判定教学设计
课题 6.2.2平行四边形的判定 单元 6 学科 数学 年级 八
教材分析 本节课是平行四边形的判定的第二课时,是在平行四边形的定义、性质的基础上又学行四边形的判定方法后进行学习的,在教学内容上起着承上启下的作用.“承上”,首先,在探究判定定理的证明方法和运用判定定理时,用到了前一节课的探究方法及证明;其次,平行四边形的判定定理和性质定理是两两对应的互逆定理; “启下”,首先,平行四边形的性质定理、判定定理是研究特殊的平行四边形的基础;其次,平行四边形性质、判定的探究模式从方法上为研究特殊的平行四边形奠定了基础.并且,本节内容还是学生运用化归思想、数学建模思想的良好素材,培养了学生的创新思维和探索精神.
核心素养分析 经历探索、猜想、证明的过程,体会归纳、类比、转化等思想,通过平行四边形判定条件的探索,培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情.
学习 目标 1.会证明对角线互相平分的四边形是平行四边形这一判定定理. 2.理解对角线互相平分的四边形是平行四边形这一判定定理,并学会简单运用.
重点 平行四边形判定方法的探究、运用
难点 对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用..
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 我们学习了哪些平行四边形的判定方法? 两组对边分别平行的四边形是平行四边形; 两组对边分别相等的四边形是平行四边形; 一组对边平行且相等的四边形是平行四边形. 猜想:对角线互相平分的四边形是平行四边形吗? 思考,回答问题 通过复习回顾,加深学生对所学知识的掌握,为这节课做好铺垫.
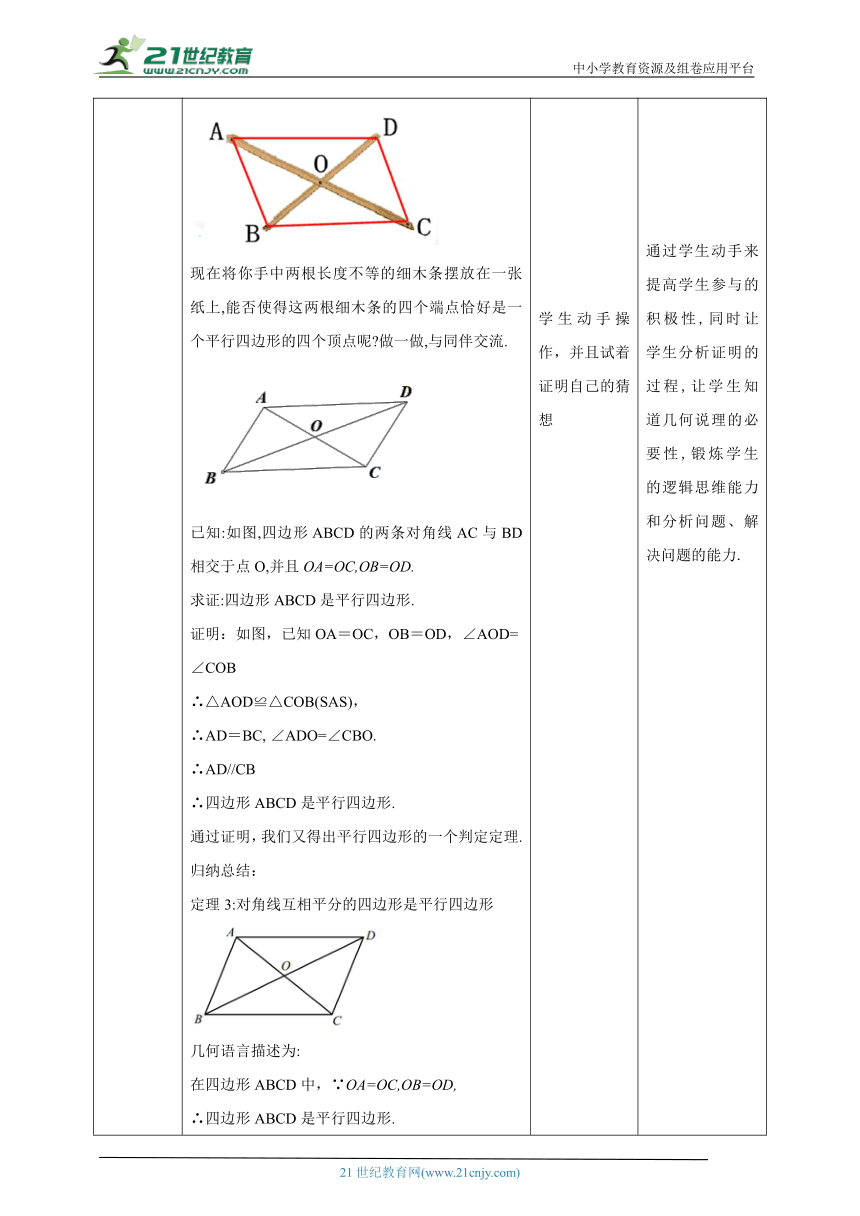
讲授新课 有一名同学将两根木条的中点重叠,并用钉子固定,得到如图的四边形,你认为这个四边形是平行四边形吗? 现在将你手中两根长度不等的细木条摆放在一张纸上,能否使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点呢 做一做,与同伴交流. 已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 证明:如图,已知OA=OC,OB=OD,∠AOD=∠COB ∴△AOD≌△COB(SAS), ∴AD=BC, ∠ADO=∠CBO. ∴AD//CB ∴四边形ABCD是平行四边形. 通过证明,我们又得出平行四边形的一个判定定理. 归纳总结: 定理3:对角线互相平分的四边形是平行四边形 几何语言描述为: 在四边形ABCD中,∵OA=OC,OB=OD, ∴四边形ABCD是平行四边形. 典例精析 例2:已知,如图6-13(1),在平行四边形ABCD中,点E、F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形吗? 证明: 如图,连接BD,交AC于点O. ∵ 四边形ABCD是平行四边形 ∴ OA=OC,OB=OD. 又∵AE=CF ∴OA-AE=OC-CF,即OE=OF. ∴四边形BFDE是平行四边形. (对角线互相平分的四边形是平行四边形) 练一练: 填空:如图在四边形ABCD中 (1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形; (2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形; (3)若对角线AC、BD交于点O,OA=OC=3,OB=5, 补充条件 ,使四边形ABCD为平行四边形. 典例精析 例、两组对角分别相等的四边形是平行四边形吗?说明理由. 证明:∵∠A+∠B+∠C+∠D=360° ∠A=∠C, ∠B=∠D ∴2∠A+2∠B=360° ∴∠A+∠B=180° ∴AD//BC ∠A+∠D=180° ∴AB//CD ∴四边形是ABCD平行四边形 归纳总结: 平行四边形判定定理: 两组对角分别相等的四边形是平行四边形 几何语言: ∵ ∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形 学生发言互相补充,归纳 学生动手操作,并且试着证明自己的猜想 学生思考,自主解答 学生填空 学生证明并得出另一个定理 通过问题的形式引导学生思考利用对角线判断平行四边形的方法, 通过学生动手来提高学生参与的积极性,同时让学生分析证明的过程,让学生知道几何说理的必要性,锻炼学生的逻辑思维能力和分析问题、解决问题的能力. 借助例题巩固平行四边形的新判定方法,同时给学生充足的时间进行书写,从而提高学生做题的规范性. 通过习题让学生巩固对角线互相平分的四边形是平行四边形的判定定理,提高学生的认知水平,灵活利用判定方法解决问题,提高学生解决问题的能力. 进一步提高学生的能力,完善知识。
课堂练习 1、下列给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判断四边形ABCD是平行四边形的是( ) A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2 2. 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法: ①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( ) ①② B.①③ C.②③ D.②③ 3.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO,请添加一个条件:____________(只添一个即可),使四边形ABCD是平行四边形. 4.如图,在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为 。 5.如图,在 ABCD中,分别过A,C两点作对角线BD的垂线,垂足分别为M,N.连接AN,CM.. 求证:(1)BM=DN; (2)四边形AMCN为平行四边形. 学生定时训练,自主解答,老师订正 针对本课时的重难点分层次进行检测,达到学有所成、了解课堂学习效果的目的.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 6.2.2平行四边形的判定 判定定理3: 对角线互相平分的四边形是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.2.2平行四边形的判定教学设计
课题 6.2.2平行四边形的判定 单元 6 学科 数学 年级 八
教材分析 本节课是平行四边形的判定的第二课时,是在平行四边形的定义、性质的基础上又学行四边形的判定方法后进行学习的,在教学内容上起着承上启下的作用.“承上”,首先,在探究判定定理的证明方法和运用判定定理时,用到了前一节课的探究方法及证明;其次,平行四边形的判定定理和性质定理是两两对应的互逆定理; “启下”,首先,平行四边形的性质定理、判定定理是研究特殊的平行四边形的基础;其次,平行四边形性质、判定的探究模式从方法上为研究特殊的平行四边形奠定了基础.并且,本节内容还是学生运用化归思想、数学建模思想的良好素材,培养了学生的创新思维和探索精神.
核心素养分析 经历探索、猜想、证明的过程,体会归纳、类比、转化等思想,通过平行四边形判定条件的探索,培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情.
学习 目标 1.会证明对角线互相平分的四边形是平行四边形这一判定定理. 2.理解对角线互相平分的四边形是平行四边形这一判定定理,并学会简单运用.
重点 平行四边形判定方法的探究、运用
难点 对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用..
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 我们学习了哪些平行四边形的判定方法? 两组对边分别平行的四边形是平行四边形; 两组对边分别相等的四边形是平行四边形; 一组对边平行且相等的四边形是平行四边形. 猜想:对角线互相平分的四边形是平行四边形吗? 思考,回答问题 通过复习回顾,加深学生对所学知识的掌握,为这节课做好铺垫.
讲授新课 有一名同学将两根木条的中点重叠,并用钉子固定,得到如图的四边形,你认为这个四边形是平行四边形吗? 现在将你手中两根长度不等的细木条摆放在一张纸上,能否使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点呢 做一做,与同伴交流. 已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 证明:如图,已知OA=OC,OB=OD,∠AOD=∠COB ∴△AOD≌△COB(SAS), ∴AD=BC, ∠ADO=∠CBO. ∴AD//CB ∴四边形ABCD是平行四边形. 通过证明,我们又得出平行四边形的一个判定定理. 归纳总结: 定理3:对角线互相平分的四边形是平行四边形 几何语言描述为: 在四边形ABCD中,∵OA=OC,OB=OD, ∴四边形ABCD是平行四边形. 典例精析 例2:已知,如图6-13(1),在平行四边形ABCD中,点E、F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形吗? 证明: 如图,连接BD,交AC于点O. ∵ 四边形ABCD是平行四边形 ∴ OA=OC,OB=OD. 又∵AE=CF ∴OA-AE=OC-CF,即OE=OF. ∴四边形BFDE是平行四边形. (对角线互相平分的四边形是平行四边形) 练一练: 填空:如图在四边形ABCD中 (1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形; (2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形; (3)若对角线AC、BD交于点O,OA=OC=3,OB=5, 补充条件 ,使四边形ABCD为平行四边形. 典例精析 例、两组对角分别相等的四边形是平行四边形吗?说明理由. 证明:∵∠A+∠B+∠C+∠D=360° ∠A=∠C, ∠B=∠D ∴2∠A+2∠B=360° ∴∠A+∠B=180° ∴AD//BC ∠A+∠D=180° ∴AB//CD ∴四边形是ABCD平行四边形 归纳总结: 平行四边形判定定理: 两组对角分别相等的四边形是平行四边形 几何语言: ∵ ∠A=∠C,∠B=∠D ∴四边形ABCD是平行四边形 学生发言互相补充,归纳 学生动手操作,并且试着证明自己的猜想 学生思考,自主解答 学生填空 学生证明并得出另一个定理 通过问题的形式引导学生思考利用对角线判断平行四边形的方法, 通过学生动手来提高学生参与的积极性,同时让学生分析证明的过程,让学生知道几何说理的必要性,锻炼学生的逻辑思维能力和分析问题、解决问题的能力. 借助例题巩固平行四边形的新判定方法,同时给学生充足的时间进行书写,从而提高学生做题的规范性. 通过习题让学生巩固对角线互相平分的四边形是平行四边形的判定定理,提高学生的认知水平,灵活利用判定方法解决问题,提高学生解决问题的能力. 进一步提高学生的能力,完善知识。
课堂练习 1、下列给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判断四边形ABCD是平行四边形的是( ) A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2 2. 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法: ①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( ) ①② B.①③ C.②③ D.②③ 3.如图,四边形ABCD的对角线AC,BD相交于点O,AO=CO,请添加一个条件:____________(只添一个即可),使四边形ABCD是平行四边形. 4.如图,在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为 。 5.如图,在 ABCD中,分别过A,C两点作对角线BD的垂线,垂足分别为M,N.连接AN,CM.. 求证:(1)BM=DN; (2)四边形AMCN为平行四边形. 学生定时训练,自主解答,老师订正 针对本课时的重难点分层次进行检测,达到学有所成、了解课堂学习效果的目的.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 6.2.2平行四边形的判定 判定定理3: 对角线互相平分的四边形是平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
