平面与平面垂直的判定
图片预览


文档简介
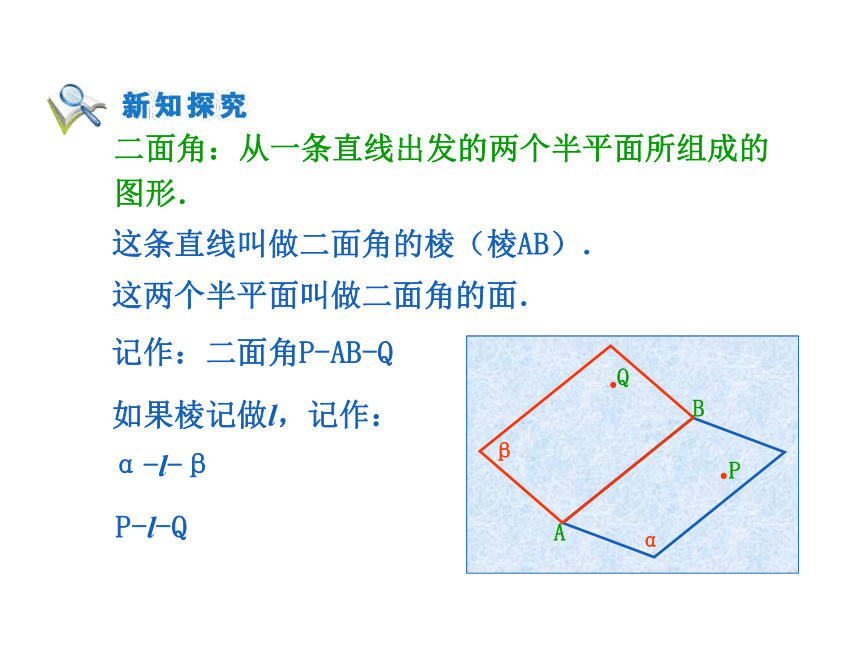
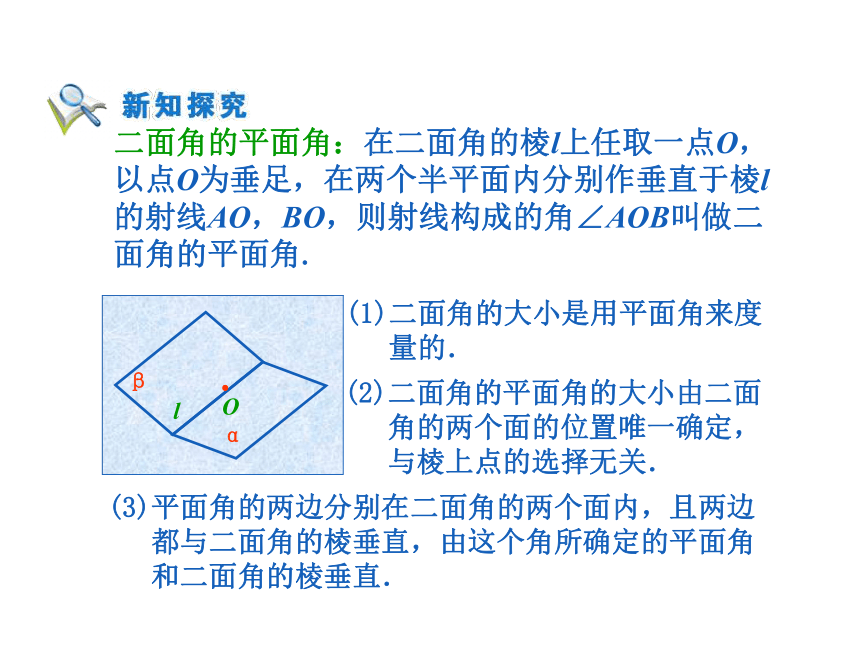
课件12张PPT。 建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙面与地面垂直. 二面角:从一条直线出发的两个半平面所组成的图形. 这条直线叫做二面角的棱(棱AB). 这两个半平面叫做二面角的面. 记作:二面角P-AB-Q 如果棱记做l,记作:α-l-β P-l-Q 二面角的平面角:在二面角的棱l上任取一点O,以点O为垂足,在两个半平面内分别作垂直于棱l的射线AO,BO,则射线构成的角∠AOB叫做二面角的平面角. (1)二面角的大小是用平面角来度
量的.(2)二面角的平面角的大小由二面
角的两个面的位置唯一确定,
与棱上点的选择无关.(3)平面角的两边分别在二面角的两个面内,且两边
都与二面角的棱垂直,由这个角所确定的平面角
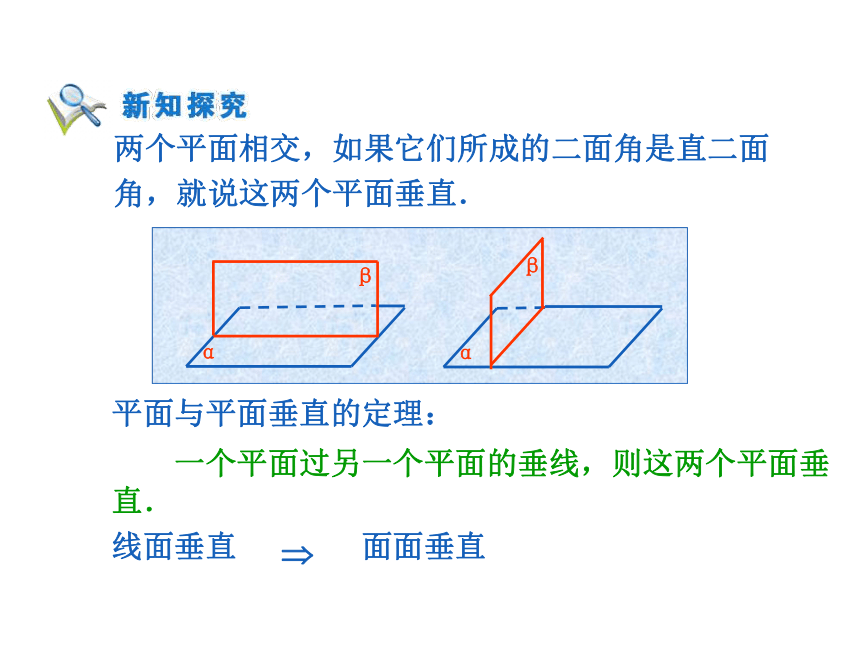
和二面角的棱垂直. ABO.两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直. 平面与平面垂直的定理: 一个平面过另一个平面的垂线,则这两个平面垂
直.AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆
周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC 证明:设⊙O所在的平面为α,因为点C是圆周上不同于A,B的
任意一点,所以∠BCA是直角, 又因为PA与AC是△PAC所在平面内
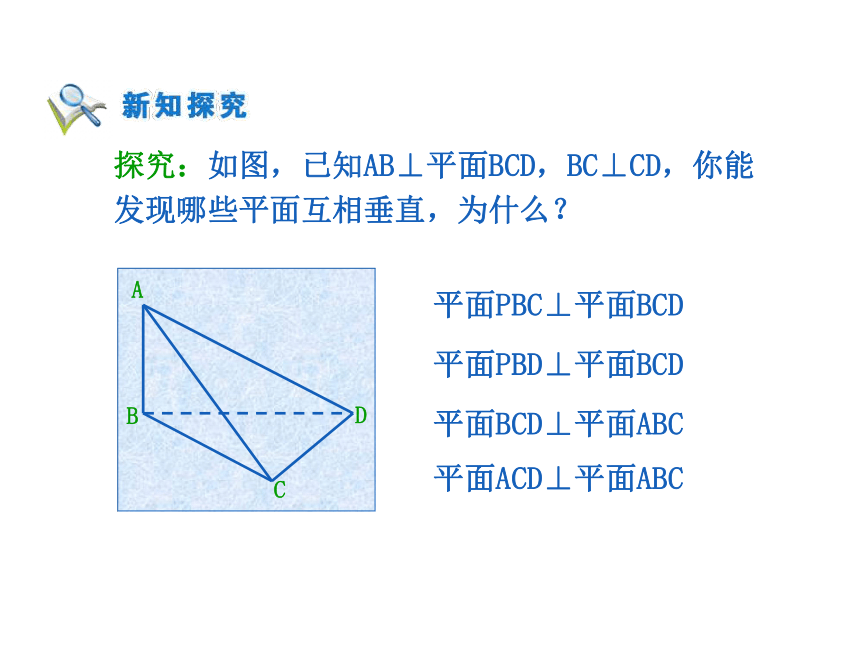
的两条相交直线,所以BC⊥平面PAC. 所以平面PAC⊥平面PBC. 即BC⊥AC;由已知条件:PA⊥α,BC在α内,所以PA⊥BC AB是的⊙O的直径 探究:如图,已知AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?平面PBC⊥平面BCD 平面PBD⊥平面BCD 平面BCD⊥平面ABC 平面ACD⊥平面ABC 如图,正方形SG1G2G3中,E,F分别是的中点,D是EF的中点,现在沿SE,SF,及EF把这个正方形折成一个四面体,使三点重合,重合后的点记为G,则在四面体S-EFG中必有( ).A:SG⊥△EFG所在平面B:SD⊥△EFG所在平面C:GF⊥△SEF所在平面D:GD⊥△SEF所在平面A判断下列命题是否正确,正确的说明理由,错误的举例说明:如图,在三棱锥V-ABC中∠VAB=∠VAC=∠ABC=90°,
试判断平面VBA与平面VBC的位置关系,并说明理
由.解:因为∠VAB =∠VAC=90° 所以VA⊥AB,VA⊥VC 所以VA⊥平面ABC,VA⊥BC 因为∠ABC=90°, 所以AB⊥BC 所以BC⊥平面VBA 所以平面VBA与平面VBC垂直. 解:设AB的中点为M,连接VM,CM 因为VA=VB,AC=BC, 所以VM⊥AB,CM⊥AB, ∠VMC是二面角V-AB-C的平面
角. 所以有VM=CM=1, 所以∠VMC=60°. 又因为VA=VB=AC=BC=2, 雪花曲线 由图1那样的等边三角形开始。然后把三角
形的每条边三等分,并在每条边三分后的中段向
外作新的等边三角形,但要像图2那样去掉与原
三角形叠合的边.接着对每个等边三角形尖出的
部分继续上述过程,即在每条边三分后的中段,
像图3那样向外画新的尖形.不断重复这样的过
程,便产生了雪花曲线.雪花曲线雪花曲线令惊异的性质是:它具有有限的面积,
但却有着无限的周长!雪花曲线的周长持续增加
而没有界限,但整条曲线却可以画在一张很小的
纸上,所以它的面积是有限的,实际上其面积等
于原三角形面积的8/5倍.
量的.(2)二面角的平面角的大小由二面
角的两个面的位置唯一确定,
与棱上点的选择无关.(3)平面角的两边分别在二面角的两个面内,且两边
都与二面角的棱垂直,由这个角所确定的平面角
和二面角的棱垂直. ABO.两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直. 平面与平面垂直的定理: 一个平面过另一个平面的垂线,则这两个平面垂
直.AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆
周上不同于A,B的任意一点.求证:平面PAC⊥平面PBC 证明:设⊙O所在的平面为α,因为点C是圆周上不同于A,B的
任意一点,所以∠BCA是直角, 又因为PA与AC是△PAC所在平面内
的两条相交直线,所以BC⊥平面PAC. 所以平面PAC⊥平面PBC. 即BC⊥AC;由已知条件:PA⊥α,BC在α内,所以PA⊥BC AB是的⊙O的直径 探究:如图,已知AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?平面PBC⊥平面BCD 平面PBD⊥平面BCD 平面BCD⊥平面ABC 平面ACD⊥平面ABC 如图,正方形SG1G2G3中,E,F分别是的中点,D是EF的中点,现在沿SE,SF,及EF把这个正方形折成一个四面体,使三点重合,重合后的点记为G,则在四面体S-EFG中必有( ).A:SG⊥△EFG所在平面B:SD⊥△EFG所在平面C:GF⊥△SEF所在平面D:GD⊥△SEF所在平面A判断下列命题是否正确,正确的说明理由,错误的举例说明:如图,在三棱锥V-ABC中∠VAB=∠VAC=∠ABC=90°,
试判断平面VBA与平面VBC的位置关系,并说明理
由.解:因为∠VAB =∠VAC=90° 所以VA⊥AB,VA⊥VC 所以VA⊥平面ABC,VA⊥BC 因为∠ABC=90°, 所以AB⊥BC 所以BC⊥平面VBA 所以平面VBA与平面VBC垂直. 解:设AB的中点为M,连接VM,CM 因为VA=VB,AC=BC, 所以VM⊥AB,CM⊥AB, ∠VMC是二面角V-AB-C的平面
角. 所以有VM=CM=1, 所以∠VMC=60°. 又因为VA=VB=AC=BC=2, 雪花曲线 由图1那样的等边三角形开始。然后把三角
形的每条边三等分,并在每条边三分后的中段向
外作新的等边三角形,但要像图2那样去掉与原
三角形叠合的边.接着对每个等边三角形尖出的
部分继续上述过程,即在每条边三分后的中段,
像图3那样向外画新的尖形.不断重复这样的过
程,便产生了雪花曲线.雪花曲线雪花曲线令惊异的性质是:它具有有限的面积,
但却有着无限的周长!雪花曲线的周长持续增加
而没有界限,但整条曲线却可以画在一张很小的
纸上,所以它的面积是有限的,实际上其面积等
于原三角形面积的8/5倍.
