3.1.1倾斜角与斜率
图片预览


文档简介
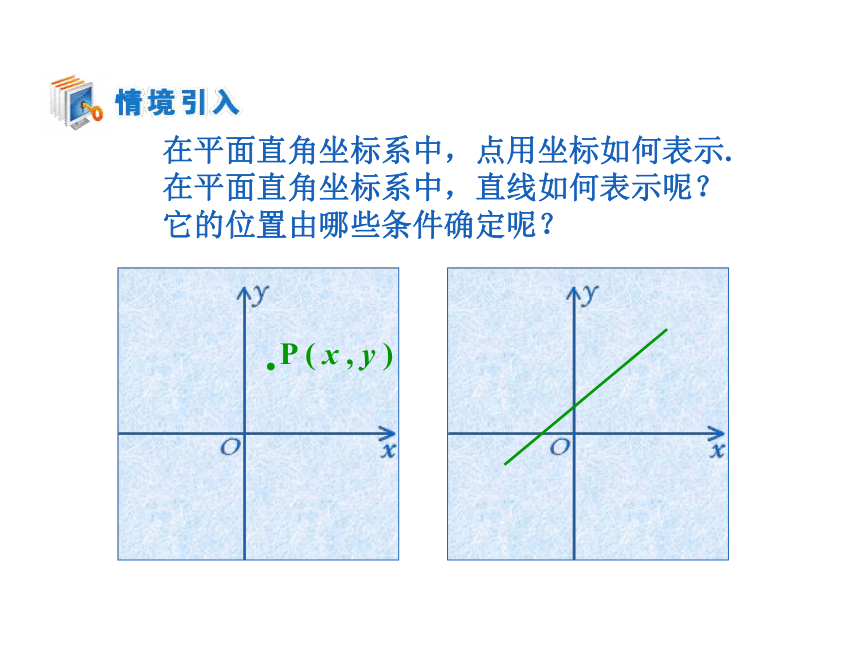
课件20张PPT。 在平面直角坐标系中,点用坐标如何表示.
在平面直角坐标系中,直线如何表示呢?
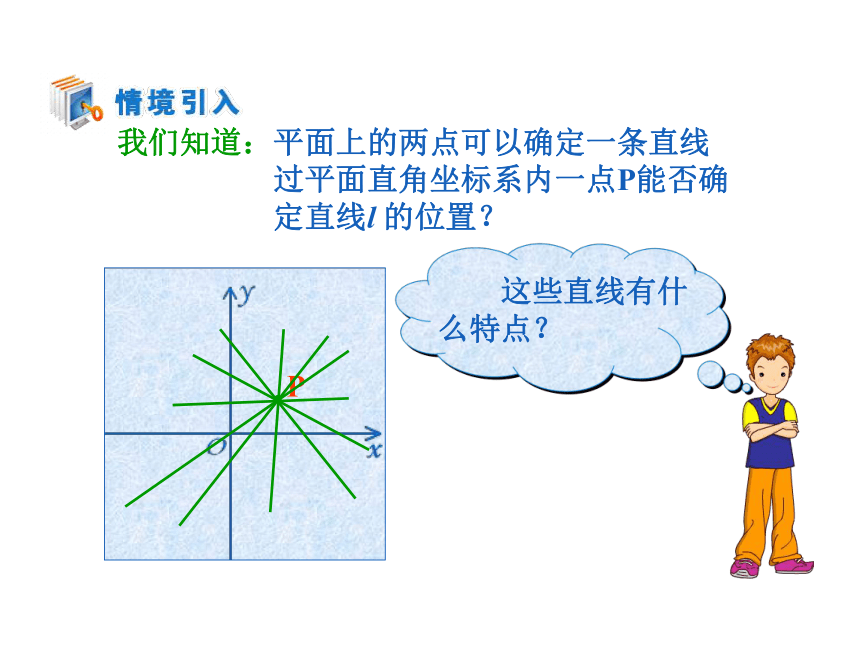
它的位置由哪些条件确定呢?我们知道:平面上的两点可以确定一条直线
过平面直角坐标系内一点P能否确
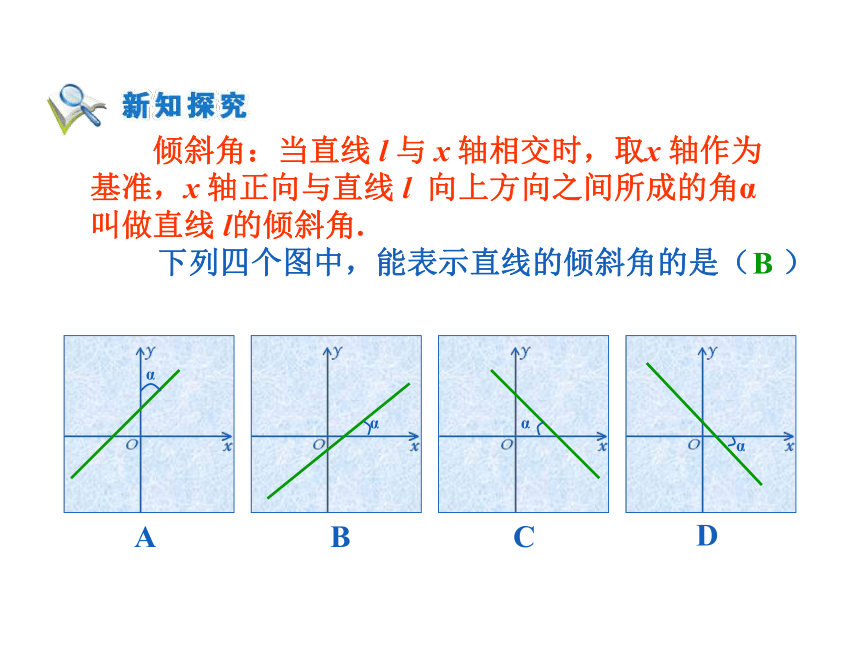
定直线l 的位置? 倾斜角:当直线 l 与 x 轴相交时,取x 轴作为
基准,x 轴正向与直线 l 向上方向之间所成的角α
叫做直线 l的倾斜角.
下列四个图中,能表示直线的倾斜角的是( )B 当直线 l 与x 轴平行或重合时,我们规定它的
倾斜角为0°.
因此,直线倾斜角的取值为:0°≤α<180°
按倾斜角进行分类,可以将直线与 x 轴所成的角分
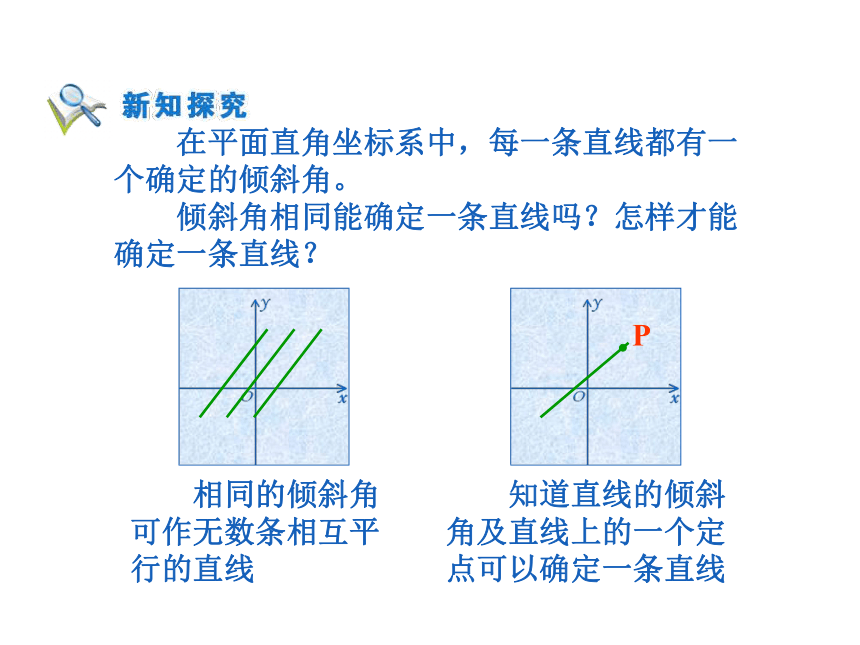
为几类? 在平面直角坐标系中,每一条直线都有一
个确定的倾斜角。
倾斜角相同能确定一条直线吗?怎样才能
确定一条直线? 相同的倾斜角
可作无数条相互平
行的直线 知道直线的倾斜
角及直线上的一个定
点可以确定一条直线 思考:日常生活中,还有没有表示倾斜程度
的量?
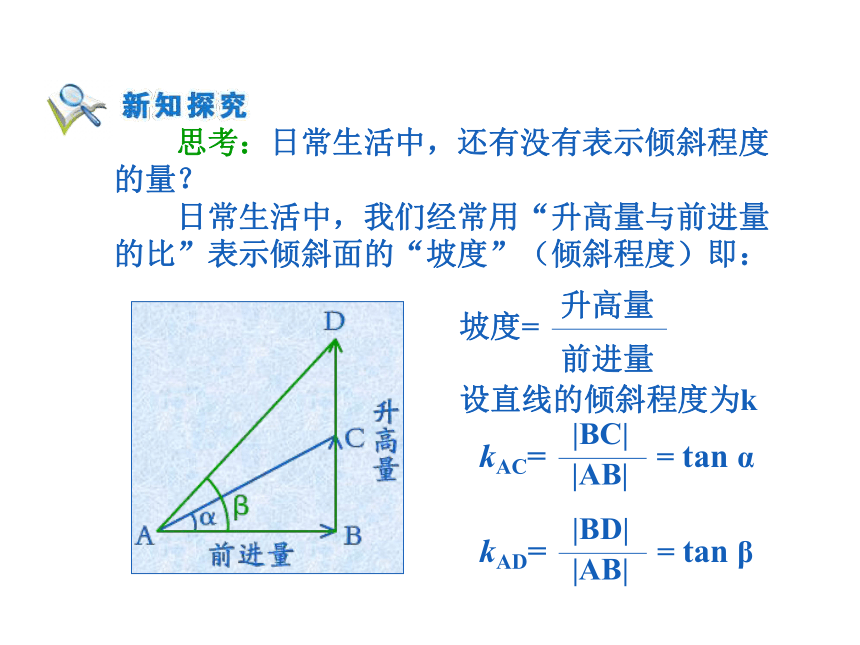
日常生活中,我们经常用“升高量与前进量
的比”表示倾斜面的“坡度”(倾斜程度)即:设直线的倾斜程度为k 斜率:一条直线的倾斜角的正切值叫做这条
直线的斜率.
斜率常用小写字母k表示α= 30° Tα= 45° Tα= 60° Tk = tan45°= 1倾斜角为90°的直线没有斜率 给定两点P1(x1 ,y1), P2 (x2 ,y2),
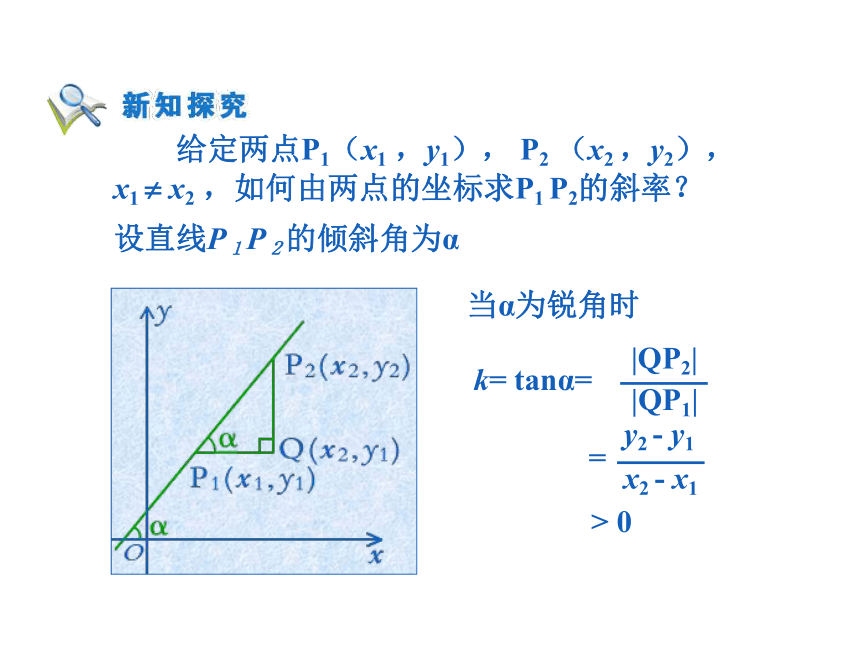
x1 1 x2 ,如何由两点的坐标求P1 P2的斜率?设直线P1P2的倾斜角为α当α为锐角时k=tanα=> 0 给定两点P1(x1 ,y1), P2 (x2 ,y2),
x1 1 x2 ,如何由两点的坐标求P1 P2的斜率?设直线P1P2的倾斜角为α当α为钝角时k=tanα=< 0tanα=
= - tanθtan(180°-θ) 给定两点P1(x1 ,y1), P2 (x2 ,y2),x 1 x2 , 当P1 P2的方向如图所示时,求 P1 P2的斜率?直线的斜率公式:
经过两点P1(x1,y1), P2(x2,y2),( x1 1 x2 )
的直线的斜率公式: 思考:
(1)当直线P1P2与x轴平行或重合时,上述式子还
成立吗?为什么?
(2)已知直线上两点A(a1,a2),B(b1,b2),
运用上述公式计算直线AB的斜率时,与A,B两点
坐标的顺序有关吗?
(3)当直线平行与y轴,或与y轴重合时,上述公
式还适用吗?为什么?
成立.因为分子为0,分母不为0.与坐标的顺序无关不适用,因为分母为0 已知A(3,2),B(-4,1),C(0,-1),
求直线AB,BC,CA的斜率,并判断这些直线的
倾斜角是锐角还是钝角。 解:直线AB的斜率kAB
直线BC的斜率kBC
直线CA的斜率kCA kAB>0, kCA>0, 所以直线AB,CA的倾斜角均为锐角
kBC<0,所以直线BC的倾斜角为钝角。 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2,-3的直线 l1,l2,l3,l4解:设A1(x1,y1)是 l1 上的一点,根据斜率公式有:即x1=y1,设x1=1,则y1=1于是
A1的坐标为(1,1).
l1是过原点及(1,1)的直线. 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2,-3的直线 l1,l2,l3,l4解: 设x2=1,则y2= -1,于是A2的
坐标为(1,-1) . 设A2(x2,y2)是 l2上的一点,同理可得出: l3是过原点及
(1,2)的直线;l4是过原点
及(1,-3)的直线 . 求经过下列两点的斜率,并判断其倾斜角是锐角还是钝角.
(1)C(18,8),D(4,-4)解:
所以直线CD的倾斜角是锐角.
所以直线PQ的倾斜角是钝角.kCD =kpq = 已知a,b,c是两两不相等的实数,求经过
下列两点的直线的倾斜角
(1) A ( a , c ) , B ( b , c ) , (2) C ( a , b ) , D ( a , c ) ,
(3) P ( b , b+c ),Q ( a , c+a )解:
所以直线AB的倾斜角为0°;
经过C,D两点的直线垂直于x轴,所以直线CD的倾斜角为90°;
所以直线PQ的倾斜角为45°. 已知直线的斜率为k=2,A(3,5),
B(x,7),C(-1,y)是这条直线上的三
个点,求x和y的值.解:因为A,B,C是同一直线上的三点,这
条直线的斜率为2
所以
解得:x=4,y= -3 .kAB== 2 ,kAC== 2 笛卡儿与解析几何
笛卡儿(1596—1650),法国数学家、 物理学家、哲学家.笛卡儿的著作,无论 是数学、自然科学,还是哲学,都开创 了这些学科的崭新时代。《几何学》是 他公开发表的唯一数学著作,虽则只有117页,但它标志着代数与几何的第一次完美结合,使形形色色的代数方程表现为不同的几何图形,许多相当难解的几何题转化为代数题后能轻而易举地找到答案. 他的主要著作都是在荷兰完成的,其中1637年出版的《方法论》一书成为哲学经典。 他的主要著作都是在荷兰完成的,其中1637年出版的《方法论》一书成为哲学经典。这本书中的3个著名附录《几何》《折光》和《气象》更奠定了笛卡儿在数学、物理和天文学中的地位。在《几何》中,笛卡儿分析了几何学与代数学的优缺点,指出:希腊人的几何过于抽象,而且过多的依赖于图形,总是要寻求一些奇妙的想法。代数却完全受法则和公式的控制,以致于阻碍了自由的思想和创造。他同时看到了几何的直观与推理的优势和代数机械化运算的力量。于是笛卡儿着手解决这个问题,并由此创立了解析几何。所以说笛卡儿是解析几何的创始人。
在平面直角坐标系中,直线如何表示呢?
它的位置由哪些条件确定呢?我们知道:平面上的两点可以确定一条直线
过平面直角坐标系内一点P能否确
定直线l 的位置? 倾斜角:当直线 l 与 x 轴相交时,取x 轴作为
基准,x 轴正向与直线 l 向上方向之间所成的角α
叫做直线 l的倾斜角.
下列四个图中,能表示直线的倾斜角的是( )B 当直线 l 与x 轴平行或重合时,我们规定它的
倾斜角为0°.
因此,直线倾斜角的取值为:0°≤α<180°
按倾斜角进行分类,可以将直线与 x 轴所成的角分
为几类? 在平面直角坐标系中,每一条直线都有一
个确定的倾斜角。
倾斜角相同能确定一条直线吗?怎样才能
确定一条直线? 相同的倾斜角
可作无数条相互平
行的直线 知道直线的倾斜
角及直线上的一个定
点可以确定一条直线 思考:日常生活中,还有没有表示倾斜程度
的量?
日常生活中,我们经常用“升高量与前进量
的比”表示倾斜面的“坡度”(倾斜程度)即:设直线的倾斜程度为k 斜率:一条直线的倾斜角的正切值叫做这条
直线的斜率.
斜率常用小写字母k表示α= 30° Tα= 45° Tα= 60° Tk = tan45°= 1倾斜角为90°的直线没有斜率 给定两点P1(x1 ,y1), P2 (x2 ,y2),
x1 1 x2 ,如何由两点的坐标求P1 P2的斜率?设直线P1P2的倾斜角为α当α为锐角时k=tanα=> 0 给定两点P1(x1 ,y1), P2 (x2 ,y2),
x1 1 x2 ,如何由两点的坐标求P1 P2的斜率?设直线P1P2的倾斜角为α当α为钝角时k=tanα=< 0tanα=
= - tanθtan(180°-θ) 给定两点P1(x1 ,y1), P2 (x2 ,y2),x 1 x2 , 当P1 P2的方向如图所示时,求 P1 P2的斜率?直线的斜率公式:
经过两点P1(x1,y1), P2(x2,y2),( x1 1 x2 )
的直线的斜率公式: 思考:
(1)当直线P1P2与x轴平行或重合时,上述式子还
成立吗?为什么?
(2)已知直线上两点A(a1,a2),B(b1,b2),
运用上述公式计算直线AB的斜率时,与A,B两点
坐标的顺序有关吗?
(3)当直线平行与y轴,或与y轴重合时,上述公
式还适用吗?为什么?
成立.因为分子为0,分母不为0.与坐标的顺序无关不适用,因为分母为0 已知A(3,2),B(-4,1),C(0,-1),
求直线AB,BC,CA的斜率,并判断这些直线的
倾斜角是锐角还是钝角。 解:直线AB的斜率kAB
直线BC的斜率kBC
直线CA的斜率kCA kAB>0, kCA>0, 所以直线AB,CA的倾斜角均为锐角
kBC<0,所以直线BC的倾斜角为钝角。 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2,-3的直线 l1,l2,l3,l4解:设A1(x1,y1)是 l1 上的一点,根据斜率公式有:即x1=y1,设x1=1,则y1=1于是
A1的坐标为(1,1).
l1是过原点及(1,1)的直线. 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2,-3的直线 l1,l2,l3,l4解: 设x2=1,则y2= -1,于是A2的
坐标为(1,-1) . 设A2(x2,y2)是 l2上的一点,同理可得出: l3是过原点及
(1,2)的直线;l4是过原点
及(1,-3)的直线 . 求经过下列两点的斜率,并判断其倾斜角是锐角还是钝角.
(1)C(18,8),D(4,-4)解:
所以直线CD的倾斜角是锐角.
所以直线PQ的倾斜角是钝角.kCD =kpq = 已知a,b,c是两两不相等的实数,求经过
下列两点的直线的倾斜角
(1) A ( a , c ) , B ( b , c ) , (2) C ( a , b ) , D ( a , c ) ,
(3) P ( b , b+c ),Q ( a , c+a )解:
所以直线AB的倾斜角为0°;
经过C,D两点的直线垂直于x轴,所以直线CD的倾斜角为90°;
所以直线PQ的倾斜角为45°. 已知直线的斜率为k=2,A(3,5),
B(x,7),C(-1,y)是这条直线上的三
个点,求x和y的值.解:因为A,B,C是同一直线上的三点,这
条直线的斜率为2
所以
解得:x=4,y= -3 .kAB== 2 ,kAC== 2 笛卡儿与解析几何
笛卡儿(1596—1650),法国数学家、 物理学家、哲学家.笛卡儿的著作,无论 是数学、自然科学,还是哲学,都开创 了这些学科的崭新时代。《几何学》是 他公开发表的唯一数学著作,虽则只有117页,但它标志着代数与几何的第一次完美结合,使形形色色的代数方程表现为不同的几何图形,许多相当难解的几何题转化为代数题后能轻而易举地找到答案. 他的主要著作都是在荷兰完成的,其中1637年出版的《方法论》一书成为哲学经典。 他的主要著作都是在荷兰完成的,其中1637年出版的《方法论》一书成为哲学经典。这本书中的3个著名附录《几何》《折光》和《气象》更奠定了笛卡儿在数学、物理和天文学中的地位。在《几何》中,笛卡儿分析了几何学与代数学的优缺点,指出:希腊人的几何过于抽象,而且过多的依赖于图形,总是要寻求一些奇妙的想法。代数却完全受法则和公式的控制,以致于阻碍了自由的思想和创造。他同时看到了几何的直观与推理的优势和代数机械化运算的力量。于是笛卡儿着手解决这个问题,并由此创立了解析几何。所以说笛卡儿是解析几何的创始人。
