4.2 直线、圆的位置关系----2圆与圆的位置关系
文档属性
| 名称 | 4.2 直线、圆的位置关系----2圆与圆的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-11 16:01:56 | ||
图片预览




文档简介
课件31张PPT。4.2.2 圆与圆的位置关系高一数学备课组
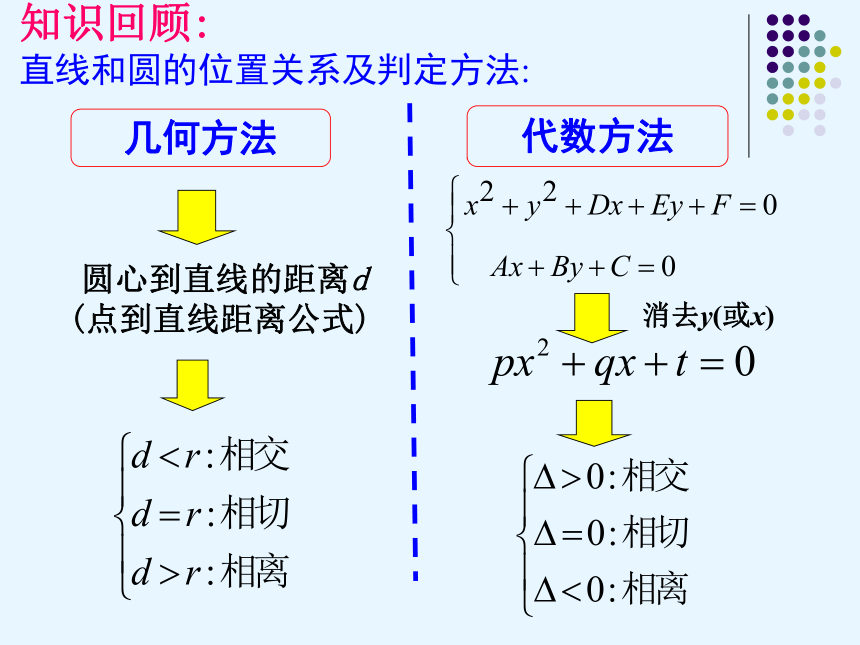
知识回顾: 直线和圆的位置关系及判定方法:几何方法 圆心到直线的距离d
(点到直线距离公式)代数方法 消去y(或x) 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 观察两圆的相对位置和交点个数1个2个1个0个0个1个2个0个1个0 圆与圆的位置关系 : 圆和圆相离 圆和圆外切圆和圆相交圆和圆内切 圆和圆内含设两圆圆心距离为d,半径分别为r1,r2交点个数
1 0 21 0 圆x2+y2=1 与 圆x2-4x+y2=0探究:圆与圆的位置关系 几何方法 圆心距d
(两点间距离公式) 比较d和r1,r2的
大小,下结论三 圆与圆的位置关系的判定:代数方法两圆的方程组成的方程组的实数解的情况 例1、设圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x
-4y-2=0,试判断圆C1与圆C2的关系. ①-②,得 x+2y-1=0, ③
由③,得解法一:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得方程④的判别式所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).解法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交,他们有两个公共点A,B. 变式1:求这两个圆的公共弦所在的直线的方程变式2:求这两个圆的公共弦长变式2:求这两个圆的公共弦长解法一:根据求得的A(-1,1),
B(3,-1)则解法二:圆心c1(-1,-4)到直线x-2y-
1=0的距离
所以
1、两圆x2+y2-6x=0和x2+y2+8y+12=0的位置关系( )
A.相离 B.外切 C.相交 D.内切
2、若圆x2+y2-2ax+a2=4和x2+y2-2bx+b2=1外离,则a,b满足的条件是____________.
3、两圆x2+y2 -2x=0与x2+y2-4y=0的公共弦所在直线的方程 ___________.
小试身手:BX-2y=0反思:判断两圆位置关系几何方法代数方法各有何优劣,如何选用?(1)当Δ=0时,有一个交点,两圆位置关系如何?内切或外切(2)当Δ<0时,没有交点,两圆位置关系如何?几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判断
圆的位置关系。内含或相离1.点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求|MN|的最大值.练一练:解:把圆的方程都化成标准形式,为
(x+3)2+(y-1)2=9
(x+1)2+(y+2)2=4
如图,C1的坐标是(-3,1),半径3;C2
的坐标是(-1,-2),半径是2,
所以,|C1C2|=
=
因此,|MN|的最大值是
MN变式: 点M在圆C1: x2+y2-8x-4y+11=0,点N在圆C2:x2+y2+4x+2y+1=0上,
求 的最小值.小结:1、研究两圆的位置关系可以有两种方法:
代数法:联立两者方程看是否有解
几何法:判断圆心距与两圆半径的和与差的绝对值的大小2、会求两圆相交时的公共弦所在的直线的方程和公共弦长。作业布置
作业:课本习题4.2 A组第4题,B组第9题
练习:课时作业本4.2.2
知识回顾: 直线和圆的位置关系及判定方法:几何方法 圆心到直线的距离d
(点到直线距离公式)代数方法 消去y(或x) 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 新课导入设想:如果把月亮与太阳看成同一平面内的两个圆,那么两个圆在作相对运动的过程中有几种位置关系产生呢? 观察两圆的相对位置和交点个数1个2个1个0个0个1个2个0个1个0 圆与圆的位置关系 : 圆和圆相离 圆和圆外切圆和圆相交圆和圆内切 圆和圆内含设两圆圆心距离为d,半径分别为r1,r2交点个数
1 0 21 0 圆x2+y2=1 与 圆x2-4x+y2=0探究:圆与圆的位置关系 几何方法 圆心距d
(两点间距离公式) 比较d和r1,r2的
大小,下结论三 圆与圆的位置关系的判定:代数方法两圆的方程组成的方程组的实数解的情况 例1、设圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x
-4y-2=0,试判断圆C1与圆C2的关系. ①-②,得 x+2y-1=0, ③
由③,得解法一:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得方程④的判别式所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).解法二: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交,他们有两个公共点A,B. 变式1:求这两个圆的公共弦所在的直线的方程变式2:求这两个圆的公共弦长变式2:求这两个圆的公共弦长解法一:根据求得的A(-1,1),
B(3,-1)则解法二:圆心c1(-1,-4)到直线x-2y-
1=0的距离
所以
1、两圆x2+y2-6x=0和x2+y2+8y+12=0的位置关系( )
A.相离 B.外切 C.相交 D.内切
2、若圆x2+y2-2ax+a2=4和x2+y2-2bx+b2=1外离,则a,b满足的条件是____________.
3、两圆x2+y2 -2x=0与x2+y2-4y=0的公共弦所在直线的方程 ___________.
小试身手:BX-2y=0反思:判断两圆位置关系几何方法代数方法各有何优劣,如何选用?(1)当Δ=0时,有一个交点,两圆位置关系如何?内切或外切(2)当Δ<0时,没有交点,两圆位置关系如何?几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判断
圆的位置关系。内含或相离1.点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求|MN|的最大值.练一练:解:把圆的方程都化成标准形式,为
(x+3)2+(y-1)2=9
(x+1)2+(y+2)2=4
如图,C1的坐标是(-3,1),半径3;C2
的坐标是(-1,-2),半径是2,
所以,|C1C2|=
=
因此,|MN|的最大值是
MN变式: 点M在圆C1: x2+y2-8x-4y+11=0,点N在圆C2:x2+y2+4x+2y+1=0上,
求 的最小值.小结:1、研究两圆的位置关系可以有两种方法:
代数法:联立两者方程看是否有解
几何法:判断圆心距与两圆半径的和与差的绝对值的大小2、会求两圆相交时的公共弦所在的直线的方程和公共弦长。作业布置
作业:课本习题4.2 A组第4题,B组第9题
练习:课时作业本4.2.2
