1.3 空间几何体的表面积与体积
文档属性
| 名称 | 1.3 空间几何体的表面积与体积 |  | |
| 格式 | zip | ||
| 文件大小 | 179.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-11 17:29:47 | ||
图片预览




文档简介
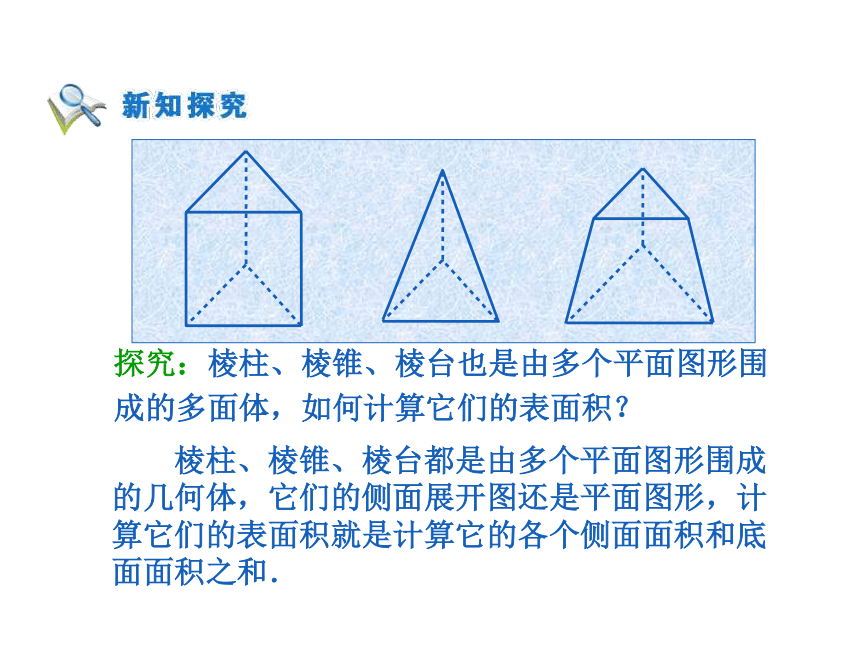
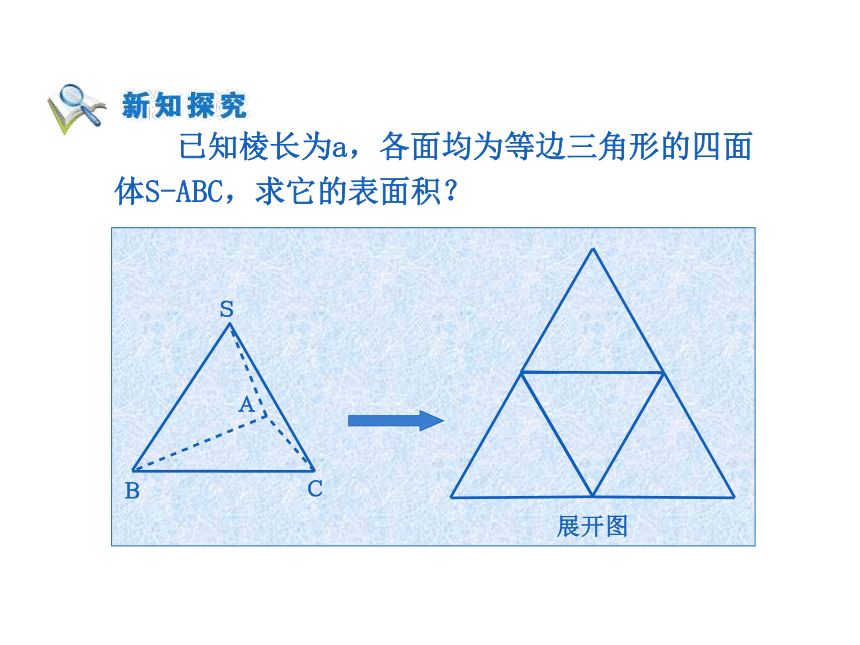
课件18张PPT。 观察这些图形,怎样求它们的表面积和体积呢?探究:棱柱、棱锥、棱台也是由多个平面图形围
成的多面体,如何计算它们的表面积? 棱柱、棱锥、棱台都是由多个平面图形围成
的几何体,它们的侧面展开图还是平面图形,计
算它们的表面积就是计算它的各个侧面面积和底
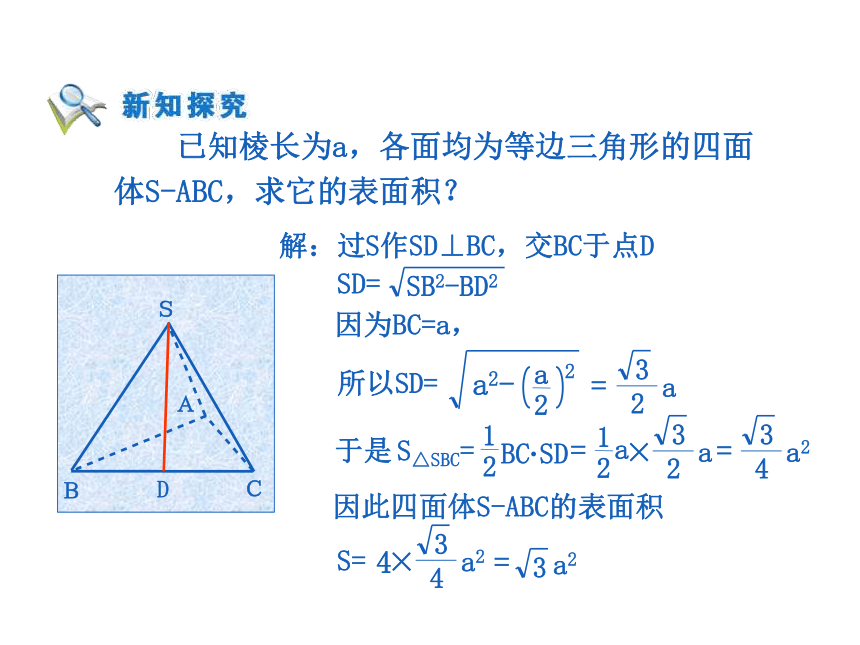
面面积之和. 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积? 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积? 解:过S作SD⊥BC,交BC于点D DSD= 因为BC=a, 因此四面体S-ABC的表面积 S= 思考:如何根据圆柱、圆锥、圆台的几何结构特征,求它们的表面积?思考:圆柱、圆锥、圆台的表面积公式之间有什么样的关系?S=π(r'2+r2+r'l+rl)r'=r时 一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为
了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取3.14,结果精确到1毫升,可用计算器)?解:花盆外壁的表面积为:答:涂100个这样的花盆约需要1000毫升油漆. 所以涂100个花盆需0.1×100×100=1000(毫升)油漆, ≈1000(cm2) =0.1(m2)思考:怎样求下列几何体的体积.V=Sh (S为底面面积,h为高)思考:怎样求下列几何体的体积.V=Sh (S为底面面积,h为高)思考:怎样求下列几何体的体积.(S为底面面积,h为高)思考:怎样求下列几何体的体积.(S为底面面积,h为高) 棱台是由棱锥截成的,圆台是由圆锥截成的,那么如何计算棱台与圆台的体积?S表示棱(圆)台下底面的面积 h表示棱台的高 比较柱体、锥体、台体的体积公式,你能发现三者之间的关系吗?V=Sh 有一堆规格相同的铁质(铁的密度是7.8g/cm3)
六角螺帽共重5.8kg,已知底面是正六边形,边长
为12mm,内孔直径为10mm,高为10mm,问这堆螺帽
大约有多少个?(π取3.14,可用计算器)解:V=V六棱柱-V圆柱≈2956(mm3)≈2956(cm3)答:这堆螺帽大约有252个. 圆锥的表面积是am3,且它的侧面展开图是一
个半圆,求这个圆锥的底面直径.解:设圆锥的地面半径为r,圆锥的表面积S =r(r+l) =a 因为圆锥的侧面展开图是一个半圆所以有l=2r, 因此有l=2r 将l=2r代入r(r+l)=a, 母线长为l; 圆锥的表面积是am3,且它的侧面展开图是一
个半圆,求这个圆锥的底面直径.那么五棱台的侧面积S侧面积 =780(cm2)答:这个五棱台的侧面积为780cm2.设垂足为OO 如图,将一个长方体沿相邻三个面的对角线
截出一个棱锥,求棱锥的体积与剩下的几何体的
体积的比?解:设长方体的长宽高分别为a,b,c则截出的三棱锥的体积 V1剩下的几何体的体积 V2
成的多面体,如何计算它们的表面积? 棱柱、棱锥、棱台都是由多个平面图形围成
的几何体,它们的侧面展开图还是平面图形,计
算它们的表面积就是计算它的各个侧面面积和底
面面积之和. 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积? 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积? 解:过S作SD⊥BC,交BC于点D DSD= 因为BC=a, 因此四面体S-ABC的表面积 S= 思考:如何根据圆柱、圆锥、圆台的几何结构特征,求它们的表面积?思考:圆柱、圆锥、圆台的表面积公式之间有什么样的关系?S=π(r'2+r2+r'l+rl)r'=r时 一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为
了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取3.14,结果精确到1毫升,可用计算器)?解:花盆外壁的表面积为:答:涂100个这样的花盆约需要1000毫升油漆. 所以涂100个花盆需0.1×100×100=1000(毫升)油漆, ≈1000(cm2) =0.1(m2)思考:怎样求下列几何体的体积.V=Sh (S为底面面积,h为高)思考:怎样求下列几何体的体积.V=Sh (S为底面面积,h为高)思考:怎样求下列几何体的体积.(S为底面面积,h为高)思考:怎样求下列几何体的体积.(S为底面面积,h为高) 棱台是由棱锥截成的,圆台是由圆锥截成的,那么如何计算棱台与圆台的体积?S表示棱(圆)台下底面的面积 h表示棱台的高 比较柱体、锥体、台体的体积公式,你能发现三者之间的关系吗?V=Sh 有一堆规格相同的铁质(铁的密度是7.8g/cm3)
六角螺帽共重5.8kg,已知底面是正六边形,边长
为12mm,内孔直径为10mm,高为10mm,问这堆螺帽
大约有多少个?(π取3.14,可用计算器)解:V=V六棱柱-V圆柱≈2956(mm3)≈2956(cm3)答:这堆螺帽大约有252个. 圆锥的表面积是am3,且它的侧面展开图是一
个半圆,求这个圆锥的底面直径.解:设圆锥的地面半径为r,圆锥的表面积S =r(r+l) =a 因为圆锥的侧面展开图是一个半圆所以有l=2r, 因此有l=2r 将l=2r代入r(r+l)=a, 母线长为l; 圆锥的表面积是am3,且它的侧面展开图是一
个半圆,求这个圆锥的底面直径.那么五棱台的侧面积S侧面积 =780(cm2)答:这个五棱台的侧面积为780cm2.设垂足为OO 如图,将一个长方体沿相邻三个面的对角线
截出一个棱锥,求棱锥的体积与剩下的几何体的
体积的比?解:设长方体的长宽高分别为a,b,c则截出的三棱锥的体积 V1剩下的几何体的体积 V2
