4.2 直线、圆的位置关系

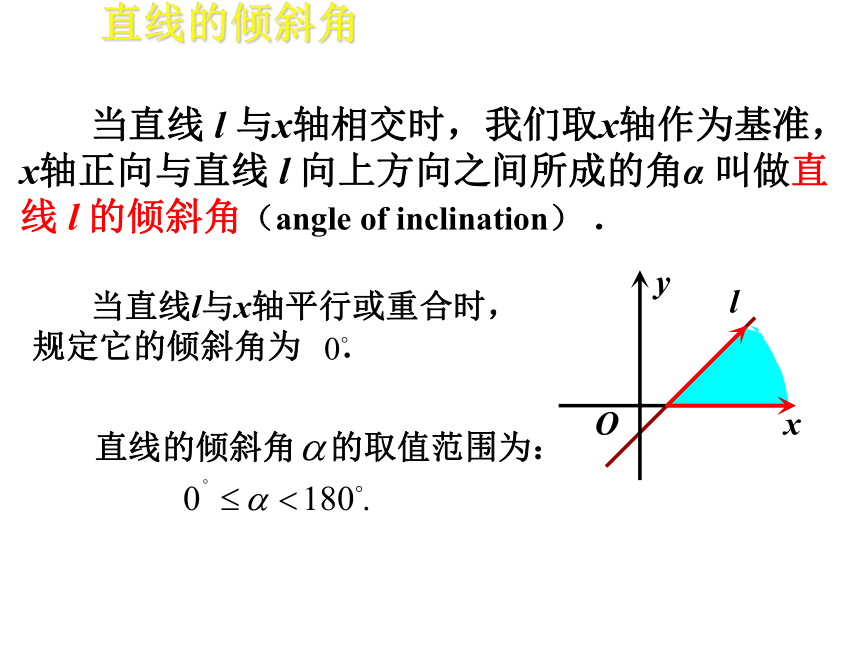
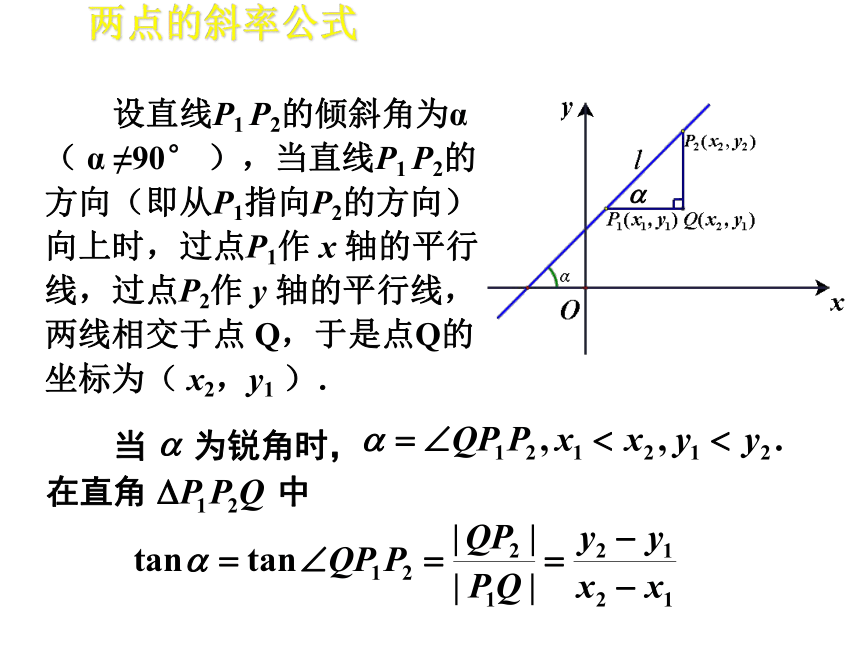
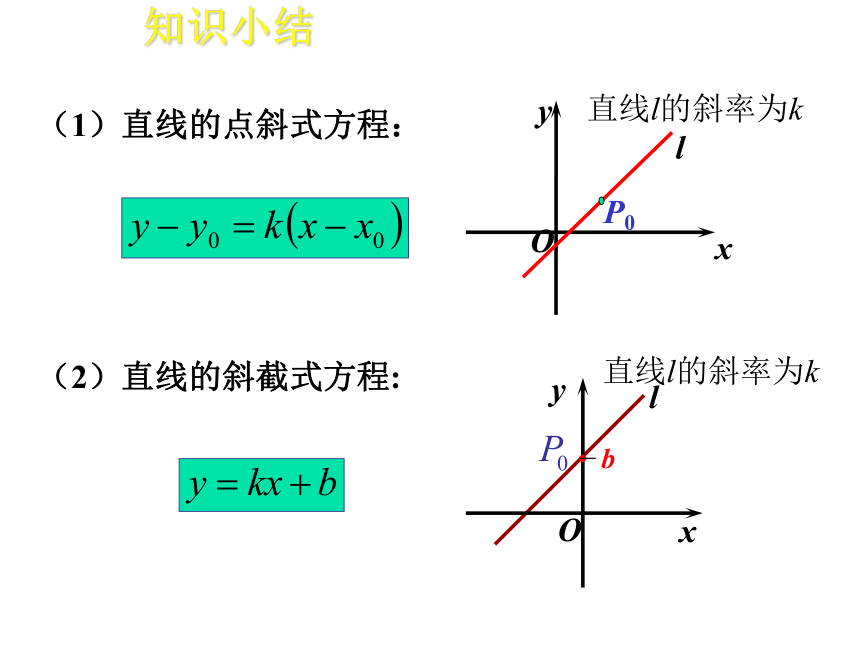
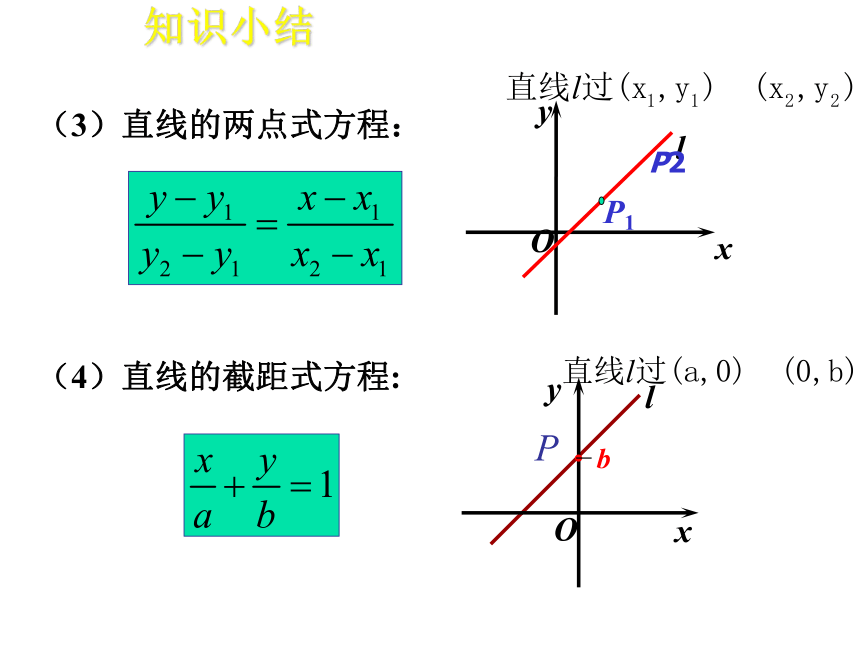
课件31张PPT。直线与圆的位置关系 当直线 l 与x轴相交时，我们取x轴作为基准，x轴正向与直线 l 向上方向之间所成的角α 叫做直线 l 的倾斜角（angle of inclination） ．xyOl 当直线l与x轴平行或重合时，规定它的倾斜角为 .直线的倾斜角 的取值范围为：直线的倾斜角 一条直线的倾斜角　的正切值叫做这条直线的斜率（slope）. 倾斜角是 的直线有斜率吗？ 倾斜角是 的直线的斜率不存在．直线的斜率　　如果使用“倾斜角”这个概念，那么这里的“坡度（比）”实际就是“倾斜角α的正切”．已知直线上两点的坐标，如何计算直线的斜率？两点的斜率公式问题 给定两点P1 （ x1 ，y1）， P2 （ x2 ，y2）， 并且x1 ≠x2，如何计算直线P1 P2的斜率k．当 为锐角时，在直角 中 设直线P1 P2的倾斜角为α（ α ≠90° ），当直线P1 P2的方向（即从P1指向P2的方向）向上时，过点P1作 x 轴的平行线，过点P2作 y 轴的平行线，两线相交于点 Q，于是点Q的坐标为（ x2，y1 ）．两点的斜率公式（1）直线的点斜式方程：（2）直线的斜截式方程:知识小结（3）直线的两点式方程：（4）直线的截距式方程:知识小结P2第一种：点斜式第二种：斜截式第三种：两点式第四种：截距式直线方程的四种形式：Ax+By+C=0这样，我们又有：关于x和y的一次方程都表示一条直线．
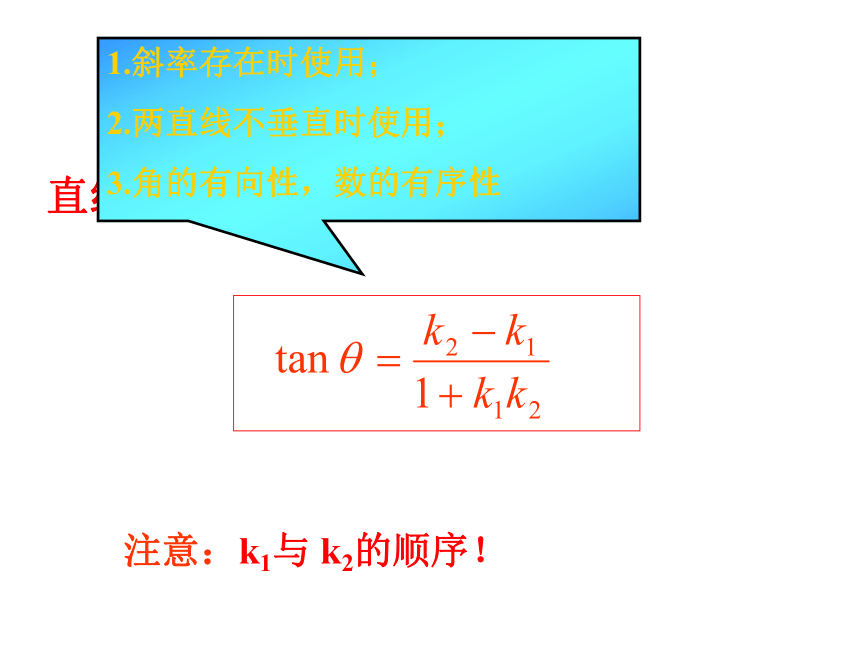
我们把方程写为直线方程的一般形式直线L1到L2的角公式：注意：k1与 k2的顺序！
1.斜率存在时使用；
2.两直线不垂直时使用；
3.角的有向性，数的有序性二、直线L1与L2的夹角：当直线L1⊥L2时，直线L1和L2的夹角是 00＜α≤900当直线L1与L2相交但不垂直时，在θ和π－θ中有且仅
有一个角是锐角，我们把其中的锐角叫两直线的夹角，
记夹角为α。直线L1与L2的夹角公式：夹角的范围：一、点关于点对称二、点关于直线对称三、直线关于点对称四、直线关于直线对称两条直线的位置关系
------对称四类对称解题要点：中点公式的运用解题要点：
法一： l 2上的任意一点的对称点在l 1上;
法二： l 1 // l 2且P到两直线等距。解题要点：求交点抓“到角”五、交点问题六、定点问题七、反射问题两条直线的位置关系
------对称常见运用例题讲解五、直线系方程例题讲解六、定点问题例题讲解七、反射问题1.直线方程的几种形式:一 .直线3.确定一条直线的条件:（1）斜率k和直线上的一个点；（2）斜率k和直线在y轴上的载距；（3）直线上的两个点；（4）直线在x，y轴上的截距；8.两直线的交点通过解方程组得到，当方程组有
唯一解时，两直线相交；当方程组无解时，两直
线平行；当方程组有无数解时，两直线重合。1.圆的标准方程是_______________,它表示的
是(x-a)2+(y-b)2=r2___________________________的圆。以C(a，b)为圆心,r为半径2.圆的一般方程是________________________________________,它表示的是__________________以C( )为x2+y2+Dx+Ey+F=0，(其中3.当D2+E2-4F=0时,方程x2+y2+Dx+Ey+F=0表示一个点( )__________________;当D2+E2-4F<0时,方程
x2+y2+Dx+Ey+F=0__________________。不表示任何图形D2+E2-4F>0)____________________________的圆。圆心,以 为半径复习 直线与圆的位置关系的判定代数方法直线方程L：Ax+By+C=0 圆的方程C：(x-a)2+(y-b)2=r2直线与圆的位置关系的判定几何方法演示小 结 分析：方法一，判断直线l与圆的位置关系，就是看由它们的方程组成的方程组有无实数解；
方法二，可以依据圆心到直线的距离与半径长的关系，判断直线与圆的位置关系． 例1 如图，已知直线l： 和圆心为C的圆 ，判断直线 l 与圆的位置关系；如果相交，求它们交点的坐标．典型例题解法一：由直线 l 与圆的方程，得：消去y，得： 例1 如图，已知直线l： 和圆心为C的圆 ，判断直线 l 与圆的位置关系；如果相交，求它们交点的坐标．典型例题因为：= 1 > 0所以，直线 l 与圆相交，有两个公共点． 解法二：圆 可化为其圆心C的坐标为（0，1），半径长为 ，点C （0，1）到直线 l 的距离所以，直线 l 与圆相交，有两个公共点．典型例题 例1 如图，已知直线l： 和圆心为C的圆 ，判断直线 l 与圆的位置关系；如果相交，求它们交点的坐标．所以，直线 l 与圆有两个交点，它们的坐标分别是：把 代入方程①，得 ；把 代入方程① ，得 ． A（2，0），B（1，3）由 ，解得： 例1 如图，已知直线l： 和圆心为C的圆 ，判断直线 l 与圆的位置关系；如果相交，求它们交点的坐标．典型例题解：解：将圆的方程写成标准形式，得：即圆心到所求直线的距离为 ．如图，因为直线l 被圆所截得的弦长是 ，所以弦心距为 例2 已知过点 的直线被圆
所截得的弦长为 ，求直线的方程．典型例题因为直线l 过点 ，即：根据点到直线的距离公式，得到圆心到直线l 的距离：因此：典型例题 例2 已知过点 的直线被圆
所截得的弦长为 ，求直线的方程．解：所以可设所求直线l 的方程为：即：两边平方，并整理得到：解得： 所以，所求直线l有两条，它们的方程分别为：或典型例题 例2 已知过点 的直线被圆
所截得的弦长为 ，求直线的方程．解：即:判断直线与圆的位置关系有两种方法： 方法一：判断直线l与圆C的方程组成的方程组是否有解．如果有解，直线l与圆C有公共点．有两组实数解时，直线l与圆C相交；有一组实数解时，直线l与圆C相切；无实数解时，直线l与圆C相离． 方法二：判断圆C的圆心到直线l的距离d与圆的半径r的关系．如果d< r ，直线l与圆C相交；如果d= r ，直线l与圆C相切；如果d> r ，直线l与圆C相离．直线与圆的位置关系 回顾我们前面提出的问题：如何用直线和圆的方程判断它们之间的位置关系？问题知识小结有无交点，有几个．直线l与圆C的方程组成的方程组是否有解，有几个解．判断圆C的圆心到直线l的距离d与圆的半径r的关系（大于、小于、等于）．判断直线与圆的位置关系