19.3矩形(区优质课课件)
图片预览




文档简介
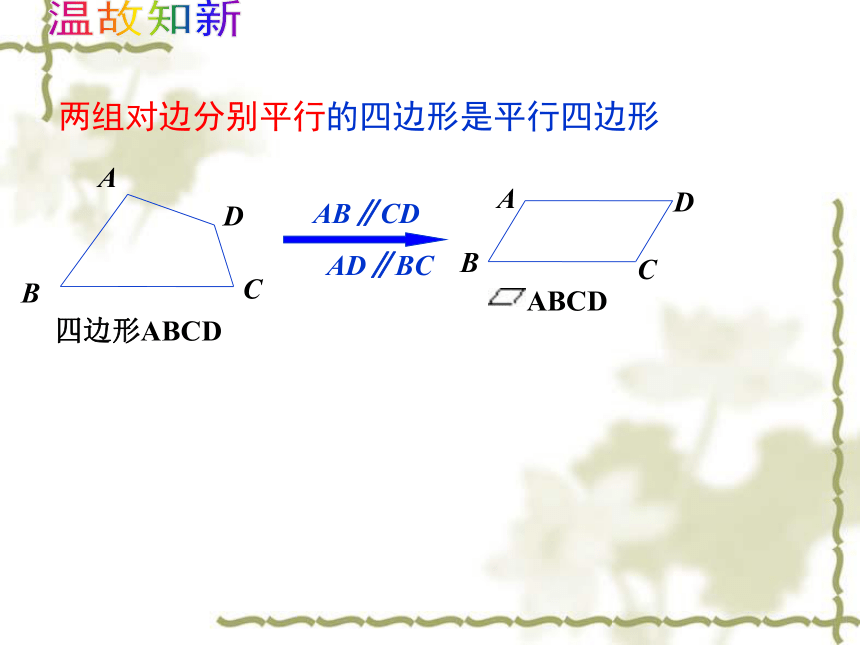
课件12张PPT。沪科版八年级数学19.3.1 矩形两组对边分别平行的四边形是平行四边形温故知新探究新知平行四边形变矩形.gsp1.矩形的定义:有一个角是直角的平行四边形是矩形一个角是直角2.矩形的表示方法:矩形ABCD探究新知 已知:四边形ABCD是矩形 , 求证:∠A= ∠B = ∠C=∠D=900 矩形的四个角都是直角猜想1矩形的性质定理1探究新知 ∴已知:在矩形ABCD中,对角线AC、BD相交于点O
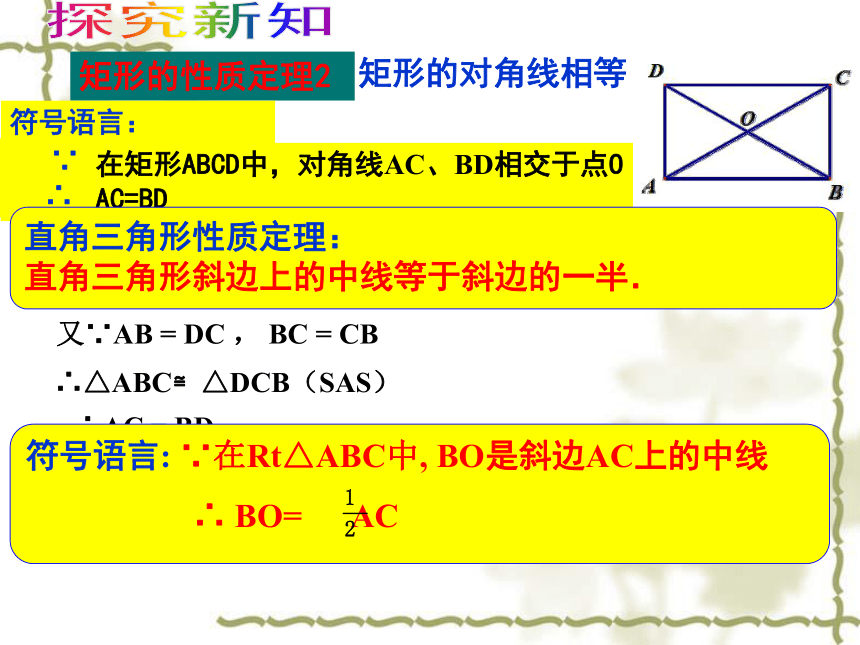
求证:AC=BD猜想2 矩形的对角线相等矩形的性质定理2探究新知 ∴直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 符号语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC 1.如图,在矩形ABCD中,已知AB=8㎝,AD=6㎝,则AC=_____㎝,OB=___㎝510小试牛刀 2.已知在Rt△ABC中,∠ABC=90°,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=________ ㎝
(2)若∠C=30°,AB=5㎝,则AC=____cm,BD=____ ㎝,∠BDC=______6510120°8例 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=60°,AD=6㎝,求矩形对角线的长再攀高峰AC=12cm,求矩形相邻两边的长9感悟收获通过本节课的学习,你有哪些收获呢?1.矩形的定义
2.矩形的性质
3.推论我学到了什么?知识 思想方法 类比思想等课后作业必做题:
1.《同步练习》19.3 基础平台一
2.预习“矩形的判定”,你能找到几种判定矩形的方法?
选做题:
矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是68cm,对角线长为10cm,求矩形的周长.再攀高峰例2.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,求△EFM的周长.解:∵ BE、CF分别是△ABC的高
∴∠BFC=90°,∠BEC=90°,
又∵M为BC的中点,∴BM=CM
∴FM=EM= BC=4,
△EFM的周长=EM+FM+EF=4+4+5=13本题考查的是矩形性质的推论,抓住推论成立的两个条件((1)直角三角形(2)斜边上的中线)是解本类题的关键.
四个角都是直角对边平行且相等对角线互相平分且相等1.矩形的定义2.矩形的性质3.推论:直角三角形斜边上的中线等于斜边的一半感悟收获轴对称图形;中心对称图形(待学)
求证:AC=BD猜想2 矩形的对角线相等矩形的性质定理2探究新知 ∴直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半. 符号语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC 1.如图,在矩形ABCD中,已知AB=8㎝,AD=6㎝,则AC=_____㎝,OB=___㎝510小试牛刀 2.已知在Rt△ABC中,∠ABC=90°,BD是斜边AC上的中线.(1)若BD=3㎝,则AC=________ ㎝
(2)若∠C=30°,AB=5㎝,则AC=____cm,BD=____ ㎝,∠BDC=______6510120°8例 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=60°,AD=6㎝,求矩形对角线的长再攀高峰AC=12cm,求矩形相邻两边的长9感悟收获通过本节课的学习,你有哪些收获呢?1.矩形的定义
2.矩形的性质
3.推论我学到了什么?知识 思想方法 类比思想等课后作业必做题:
1.《同步练习》19.3 基础平台一
2.预习“矩形的判定”,你能找到几种判定矩形的方法?
选做题:
矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是68cm,对角线长为10cm,求矩形的周长.再攀高峰例2.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,求△EFM的周长.解:∵ BE、CF分别是△ABC的高
∴∠BFC=90°,∠BEC=90°,
又∵M为BC的中点,∴BM=CM
∴FM=EM= BC=4,
△EFM的周长=EM+FM+EF=4+4+5=13本题考查的是矩形性质的推论,抓住推论成立的两个条件((1)直角三角形(2)斜边上的中线)是解本类题的关键.
四个角都是直角对边平行且相等对角线互相平分且相等1.矩形的定义2.矩形的性质3.推论:直角三角形斜边上的中线等于斜边的一半感悟收获轴对称图形;中心对称图形(待学)
