用样本的数字特征估计总体的数字特征
文档属性
| 名称 | 用样本的数字特征估计总体的数字特征 |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-11 17:42:04 | ||
图片预览









文档简介
课件32张PPT。 在一次射击比赛中,甲、乙两名运动员各射击10次,命中环数如下:
甲运动员:7,8,6,8,6,5,8,10,7,4;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗? 为了从整体上更好地把握总体的规律,我们
要通过样本的数据对总体的数字特征进行研究.(1)怎样将各个样本数据汇总为一个数值,并
使它成为样本数据的“中心点”?
(2)能否用一个数值来描写样本数据的离散程
度?(让学生回忆初中所学的一些统计知识,思
考后展开讨论)众数,中位数,平均数
众数,中位数,平均数等都能够为我们提供
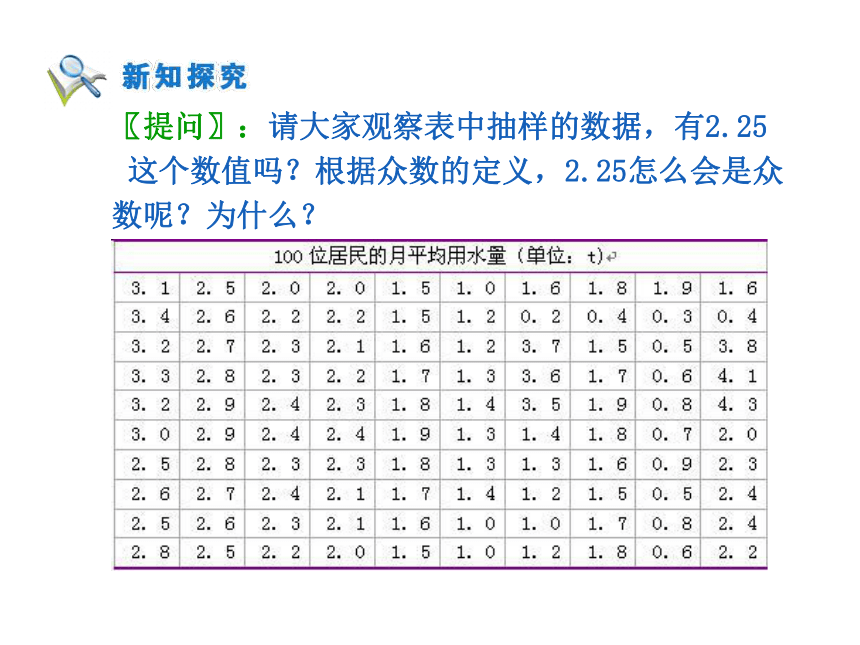
关于样本数据的特征信息. 如在调查100位居民的月均用水量问题的频率 分布直方图: 从这些样本数据的频率分布直方图可以看出,
月均用水量的众数是2.25t(最高的矩形的中点)
它告诉我们,该市的月均用水量为2.25t的居民
数比月均用水量为其他值的居民数多,但它并没
有告诉我们到底多多少. 〖提问〗:请大家观察表中抽样的数据,有2.25
?这个数值吗?根据众数的定义,2.25怎么会是众
数呢?为什么? 分析:这是因为样本数据的频率分布直方图把原
始的一些数据给遗失的原因,而2.25是由样本数
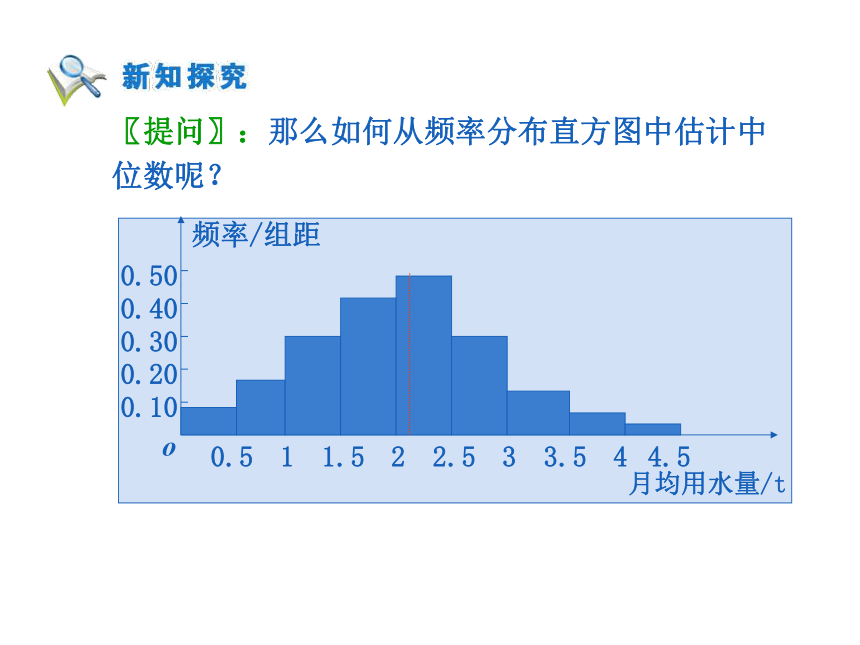
据的频率分布直方图得来的,所以存在一些偏差. 〖提问〗:那么如何从频率分布直方图中估计中
位数呢?分析:在样本数据中,有50% 的个体小于或等于
中位数,也有50% 的个体大于或等于中位数.因
此,在频率分布直方图中,矩形的面积大小正好
表示频率的大小,即中位数左边和右边的直方图
的面积应该相等.由此可以估计出中位数的值为
2.02.〖思考1〗:2.02这个中位数的估计值,与样本的
中位数值2.0不一样,你能解释其中的原因吗?原因:样本数据的频率分布直方图把原始的一些数
据给遗失了. 〖思考2〗:中位数不受少数几个极端值的影响,
这在某些情况下是一个优点,但是它对极端值的不
敏感有时也会成为缺点,你能举例说明吗? 平均数向我们提供了样本数据的重要信息,
但是平均有时也会使我们作出对总体的片面断.
因为这个平均数掩盖了一些极端的情况,而这些
极端情况显然是不能忽的.因此,只有平均数还
难以概括样本数据的实际状态. 例如,在一次射击选拔比赛中,甲、乙两名
运动员各射击10次,命中环数如下:
甲运动员:7,8,6,8,6,5,8,10,7,4;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发
挥的更稳定些吗?如果你是教练,选哪位选手去
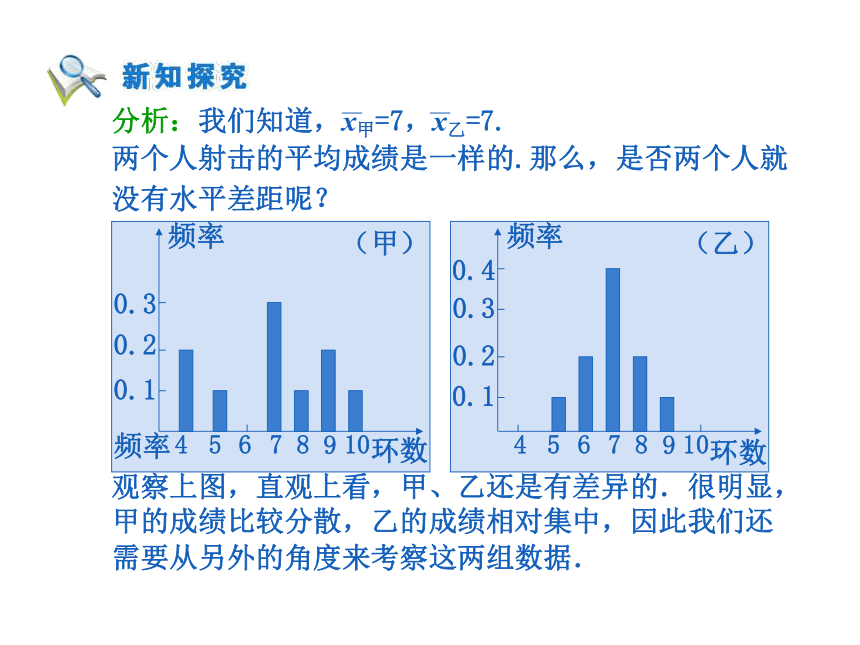
参加正式比赛? (甲)(乙)观察上图,直观上看,甲、乙还是有差异的.很明显,甲的成绩比较分散,乙的成绩相对集中,因此我们还
需要从另外的角度来考察这两组数据. 标准差
考察样本数据的分散程度的大小,最常用的
统计量是标准差.标准差是样本数据到平均数的
一种平均距离,一般用s表示.(4)算出(3)中n个平方数的平均数,即为样
本方差. 显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小.〖提问〗:标准差的取值范围是什么?标准差为
0的样本数据有什么特点?分析:从标准差的定义和计算公式都可以得出:
s≥0.当s=0时,意味着所有的样本数据都等于样
本平均数. 用计算器可算出甲,乙两人的的成绩的标准差:s甲=2,s乙≈1.095.由可以知道,甲的成绩离
散程度大,乙的成绩离散程度小.由此可以估计,乙比甲的射击成绩稳定. 甲、乙两组数据的离散程度与标准差之间的关系可用下图直观地表示出来.〖例1〗:画出下列四组样本数据的直方图,说
明他们的异同点.
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8分析:先画出数据的直方图,根据样本数据算出
样本数据的平均数,利用标准差的计算公式即可
算出每一组数据的标准差.解:四组样本数据的直方图是:(1)(2)(3)(4) 四组数据的平均数都是5.0,标准差分别为:0.00,0.82,1.48,2.83.他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是
不一样的. 〖例2〗:甲乙两人同时生产内径为25.40mm的一种
零件.为了对两人的生产质量进行评比,从他们生产
的零件中各抽出20件,量得其内径尺寸如下(单位:mm): 甲
25.46,25.32,25.45,25.39,25.36
25.34,25.42,25.45,25.38,25.42
25.39,25.43,25.39,25.40,25.44
25.40,25.42,25.35,25.41,25.39 乙
25.40,25.43,25.44,25.48,25.48
25.47,25.49,25.49,25.36,25.34
25.33,25.43,25.43,25.32,25.47
25.31,25.32,25.32,25.32,25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析:每一个工人生产的所有零件的内径尺寸组
成一个总体,由于零件的生产标准已经给出(内
径25.40mm),生产质量可以从总体的平均数与标
准差两个角度来衡量.根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得:
x甲≈25.401,x乙≈25.406;s甲0.037,
s乙≈0.068
从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于,因此甲生产的零件内径比乙的稳定程度高很多.于是,可以作出判断,甲生产的零件的质量比乙的高一些. 选择题:
1.在统计中,样本的标准差可以近似地反映总体
的 ( )
A. 平均状态 B. 分布规律
C. 波动大小 D. 最大值和最小值
2.频率分布直方图的重心是 ( )
A. 众数 B. 中位数
C. 标准差 D. 平均数
3.能反映一组数据的离散程度的是 ( )
A. 众数 B. 平均数
C. 标准差 D. 极差CDC4.与原数据单位不一样的是 ( )
A. 众数 B. 平均数
C. 标准差 D. 方差
5.下列数字特征一定是数据组中数据的是( )
A. 众数 B. 中位数
C. 标准差 D. 平均数
6. 频率分布直方图中最高小矩形的中间位置所对的数字特征是 ( )
A. 中位数 B. 众数
C. 平均数 D. 标准差DAB解答题
1. 据报道,某公司的33名职工的月工资(以元为
单位)如下:(1)求该公司职工月工资的平均数,中位数,众数;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数,中位数,众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?(3)在这个问题中,中位数或众数均能反映公
司员工的工资水平.因为公司中少数人的工资额
与大多数人的工资额差别较大,这样导致平均数
偏差较大,所以平均数不能反映这个公司工资水平. 2.甲、乙两种玉米苗中各抽10株,分别测得它
们的株高如下(单位:cm):
甲:25 41 40 37 22 14 19 39 21 42
乙:27 16 44 27 44 16 40 40 16 40
问:(1)哪种玉米的苗长得高?(2)哪种玉
米的苗长得齐?
甲运动员:7,8,6,8,6,5,8,10,7,4;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发挥的更稳定些吗? 为了从整体上更好地把握总体的规律,我们
要通过样本的数据对总体的数字特征进行研究.(1)怎样将各个样本数据汇总为一个数值,并
使它成为样本数据的“中心点”?
(2)能否用一个数值来描写样本数据的离散程
度?(让学生回忆初中所学的一些统计知识,思
考后展开讨论)众数,中位数,平均数
众数,中位数,平均数等都能够为我们提供
关于样本数据的特征信息. 如在调查100位居民的月均用水量问题的频率 分布直方图: 从这些样本数据的频率分布直方图可以看出,
月均用水量的众数是2.25t(最高的矩形的中点)
它告诉我们,该市的月均用水量为2.25t的居民
数比月均用水量为其他值的居民数多,但它并没
有告诉我们到底多多少. 〖提问〗:请大家观察表中抽样的数据,有2.25
?这个数值吗?根据众数的定义,2.25怎么会是众
数呢?为什么? 分析:这是因为样本数据的频率分布直方图把原
始的一些数据给遗失的原因,而2.25是由样本数
据的频率分布直方图得来的,所以存在一些偏差. 〖提问〗:那么如何从频率分布直方图中估计中
位数呢?分析:在样本数据中,有50% 的个体小于或等于
中位数,也有50% 的个体大于或等于中位数.因
此,在频率分布直方图中,矩形的面积大小正好
表示频率的大小,即中位数左边和右边的直方图
的面积应该相等.由此可以估计出中位数的值为
2.02.〖思考1〗:2.02这个中位数的估计值,与样本的
中位数值2.0不一样,你能解释其中的原因吗?原因:样本数据的频率分布直方图把原始的一些数
据给遗失了. 〖思考2〗:中位数不受少数几个极端值的影响,
这在某些情况下是一个优点,但是它对极端值的不
敏感有时也会成为缺点,你能举例说明吗? 平均数向我们提供了样本数据的重要信息,
但是平均有时也会使我们作出对总体的片面断.
因为这个平均数掩盖了一些极端的情况,而这些
极端情况显然是不能忽的.因此,只有平均数还
难以概括样本数据的实际状态. 例如,在一次射击选拔比赛中,甲、乙两名
运动员各射击10次,命中环数如下:
甲运动员:7,8,6,8,6,5,8,10,7,4;
乙运动员:9,5,7,8,7,6,8,6,7,7.
观察上述样本数据,你能判断哪个运动员发
挥的更稳定些吗?如果你是教练,选哪位选手去
参加正式比赛? (甲)(乙)观察上图,直观上看,甲、乙还是有差异的.很明显,甲的成绩比较分散,乙的成绩相对集中,因此我们还
需要从另外的角度来考察这两组数据. 标准差
考察样本数据的分散程度的大小,最常用的
统计量是标准差.标准差是样本数据到平均数的
一种平均距离,一般用s表示.(4)算出(3)中n个平方数的平均数,即为样
本方差. 显然,标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小.〖提问〗:标准差的取值范围是什么?标准差为
0的样本数据有什么特点?分析:从标准差的定义和计算公式都可以得出:
s≥0.当s=0时,意味着所有的样本数据都等于样
本平均数. 用计算器可算出甲,乙两人的的成绩的标准差:s甲=2,s乙≈1.095.由可以知道,甲的成绩离
散程度大,乙的成绩离散程度小.由此可以估计,乙比甲的射击成绩稳定. 甲、乙两组数据的离散程度与标准差之间的关系可用下图直观地表示出来.〖例1〗:画出下列四组样本数据的直方图,说
明他们的异同点.
(1)5,5,5,5,5,5,5,5,5
(2)4,4,4,5,5,5,6,6,6
(3)3,3,4,4,5,6,6,7,7
(4)2,2,2,2,5,8,8,8,8分析:先画出数据的直方图,根据样本数据算出
样本数据的平均数,利用标准差的计算公式即可
算出每一组数据的标准差.解:四组样本数据的直方图是:(1)(2)(3)(4) 四组数据的平均数都是5.0,标准差分别为:0.00,0.82,1.48,2.83.他们有相同的平均数,但他们有不同的标准差,说明数据的分散程度是
不一样的. 〖例2〗:甲乙两人同时生产内径为25.40mm的一种
零件.为了对两人的生产质量进行评比,从他们生产
的零件中各抽出20件,量得其内径尺寸如下(单位:mm): 甲
25.46,25.32,25.45,25.39,25.36
25.34,25.42,25.45,25.38,25.42
25.39,25.43,25.39,25.40,25.44
25.40,25.42,25.35,25.41,25.39 乙
25.40,25.43,25.44,25.48,25.48
25.47,25.49,25.49,25.36,25.34
25.33,25.43,25.43,25.32,25.47
25.31,25.32,25.32,25.32,25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析:每一个工人生产的所有零件的内径尺寸组
成一个总体,由于零件的生产标准已经给出(内
径25.40mm),生产质量可以从总体的平均数与标
准差两个角度来衡量.根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得:
x甲≈25.401,x乙≈25.406;s甲0.037,
s乙≈0.068
从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小;从样本标准差看,由于,因此甲生产的零件内径比乙的稳定程度高很多.于是,可以作出判断,甲生产的零件的质量比乙的高一些. 选择题:
1.在统计中,样本的标准差可以近似地反映总体
的 ( )
A. 平均状态 B. 分布规律
C. 波动大小 D. 最大值和最小值
2.频率分布直方图的重心是 ( )
A. 众数 B. 中位数
C. 标准差 D. 平均数
3.能反映一组数据的离散程度的是 ( )
A. 众数 B. 平均数
C. 标准差 D. 极差CDC4.与原数据单位不一样的是 ( )
A. 众数 B. 平均数
C. 标准差 D. 方差
5.下列数字特征一定是数据组中数据的是( )
A. 众数 B. 中位数
C. 标准差 D. 平均数
6. 频率分布直方图中最高小矩形的中间位置所对的数字特征是 ( )
A. 中位数 B. 众数
C. 平均数 D. 标准差DAB解答题
1. 据报道,某公司的33名职工的月工资(以元为
单位)如下:(1)求该公司职工月工资的平均数,中位数,众数;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数,中位数,众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?(3)在这个问题中,中位数或众数均能反映公
司员工的工资水平.因为公司中少数人的工资额
与大多数人的工资额差别较大,这样导致平均数
偏差较大,所以平均数不能反映这个公司工资水平. 2.甲、乙两种玉米苗中各抽10株,分别测得它
们的株高如下(单位:cm):
甲:25 41 40 37 22 14 19 39 21 42
乙:27 16 44 27 44 16 40 40 16 40
问:(1)哪种玉米的苗长得高?(2)哪种玉
米的苗长得齐?
