1.3 算法与案例
图片预览








文档简介
课件25张PPT。 请先依次指出表格中哪些行有你的生月,然后
再依次指出表格中哪些行有你的生日,便知道你的
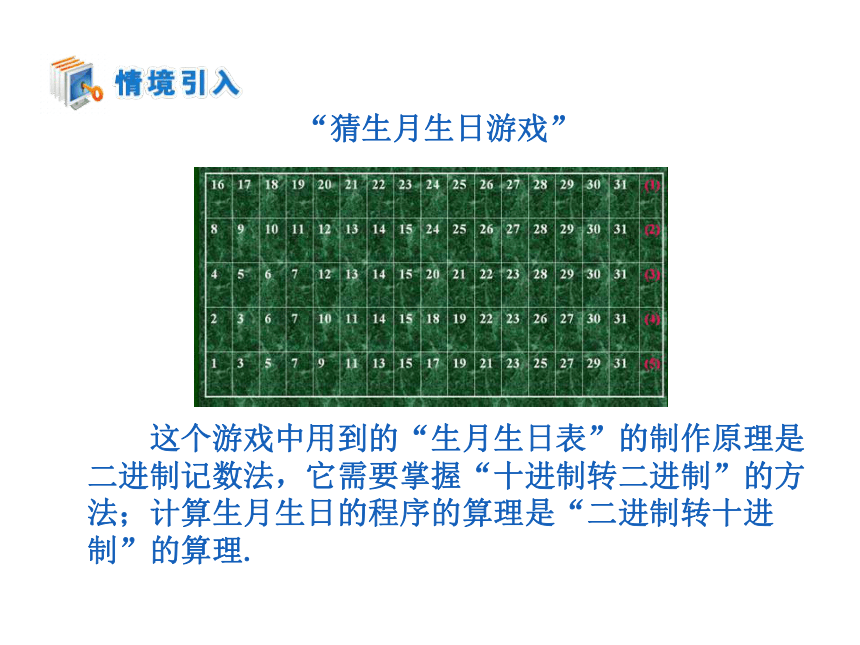
生月生日. “猜生月生日游戏” “猜生月生日游戏” 这个游戏中用到的“生月生日表”的制作原理是
二进制记数法,它需要掌握“十进制转二进制”的方
法;计算生月生日的程序的算理是“二进制转十进
制”的算理. 进位制是人们为了计数和运算方便而约定的记
数系统,约定满二进一,就是二进制;满十进一,
就是十进制;满十二进一,就是十二进制;满六十
进一,就是六十进制;等等. 即“满几进一”就是几
进制,几进制的基数(都是大于1的整数)就是几. 十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,于是可得下面的式子: 与十进制类似,其他的进位制也可以按照位置原则计数,如:110011(2)= 7342(8)= 3721=3×103+7×102+2×101+1×1001×25+1×24+0×23+0×22+1×21
+1×25 7×83+3×82+4×81+2×80 一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式.anan-1··· a1a0(k)(0写成各位上数字与的幂的乘积之和的形式吗?(anan-1··· a1a0(k) = an×kn+an-1×kn-1+···+a1×k1+a0×k0)例1:把二进制数110 011化为十进制数. 分析:先把二进制数写成不同位上数字与2
的幂的乘机之和的形式,再按照十进制数的运算
规则计算出结果.解:110011(2)=1×25+1×24+0×23+0×22
+1×21+1×25 = 1×32+1×16+1×2+1= 51练习:将下面两个非十进制数分别转化为十进制
数.(1)101001(2)(2)324(5)答案:(1)81,(2)89思考:体会“二进制转十进制”的算理,你能否设计
一个算法,把其他进位制数化为十进制数?问题:设计一个算法,把k进制数a(共有n位)化为十
进制数b. 算法分析: 从计算过程可以看出,计算k进制数a的右数
第i位数字ai与ki-1的乘积ai·ki-1,再将其累加,这
是一个重复操作的步骤,所以,可以用循环结构
来构造算法.问题:设计一个算法,把k进制数a(共有n位)化为十
进制数b. 算法步骤:
第一步,输入a,k和n的值. 第二步,将b的值初始化为0,将i的值初始化
为1.第五步,输出b的值.第三步,b=b+ai·ki-1,i=i+1. 第四步,判断i>n.若是,则执行第五步;否
则,返回第三步.程序框图: 下面我们以3721为例,探究“除10取余”的过
程: 3721=372×10+1, 372=37×10+2, 37=3×10+7, 3=0×10+3。 所以3721=10×(10×(10×3+7)+2)+1 =3×103+7×102+2×101+1×100 下面给出 “除10取余”的十进制记数法则:一个十进制数a除以10所得的商是b0,余数是a0 , 即 a=b0×10+a0,
则a0是a的个位数;
b0除以10所得的商是b1,余数是a1,
即 b0=b1×10+a1,
则a1是a的十位数.
…
一般地,bn-1除以10所得的商是bn,余数是an,
即 bn-1=bn×10+an,
则an是a的从右往左数第n+1位数. “除2取余”的二进制记数法则:一个十进制数a除以2所得的商是b0,余数是a0 , 即 a=b0×2+a0,
则a0是a的右边第一位数;
b0除以2所得的商是b1,余数是a1,
即 b0=b1×2+a1,
则a1是a的右边第二位数.
…
一般地,bn-1除以2所得的商是bn,余数是an,
即 bn-1=bn×2+an,
则an是a的从右往左数第n+1位数. 再将依次得到的余数从右到左排列,就可得
到这个2进制数. 上述方法可以推广为把十进制数转化为k进
制数的算法,称为除k取余法.思考:你能将上述算理 推广到“十进制转k进制”
吗?请写出算法步骤、程序框图和程序.算法分析: 一个十进制数a除以k所得的商是q0,余数是
r0,即:
a=q0×k+r0,
则r0是a的k进制数的右数第一位数;
若q0除以k所得的商是q1,余数是r1,即:
a=q1×k+r1,
则r1是a的k进制数的右数第二位数.
…
若qn-1除以k所得的商是0,余数是rn,即qn-1=rn,
则是a的k进制数的左数第一位数. 算法步骤:
第一步,给定十进制正整数a和转化后的数的
基数k. 第二步,求出a除以k所得的商q,余数r. 第三步,若q≠0,则a=q,返回第二步;否
则,执行第四步. 第四步,将依次得到的余数从右到走排列,
得到k进制数.程序框图:请以十进制数89为例,探究“除2取余”的过程.计算方法:89=44×2+1,
44=22×2+0, 22=11×2+0,
11=5×2+1 , 5=2×2+1,
2=1×2+0 , 1=0×2+1
所以
89=2×(2×(2×(2×(2×2+1)
+1)+0)+0)+1
=1×26+0×25+1×24+1×23
+0×23+0×21+1×20
=1011001(2)思考:你能给出“除2取余”的二进制记数法则吗? 这种算法叫做除2取余法练习:
(1)用“除k取余法”将十进制数2008转化为五进
制数和八进制数.(2)把389化成四进制数的末位为( )(A) 1 (B) 2 (C) 3 (D) 0 A 答案:31013(5),3730(8) 思考: 如何把二进制数1011001化为五进制数. 分析:要在非十进制之间实现转化,一个自然
的想法是利用十进制作桥梁.先将二进制数转化为
十进制数,在将十进制数转化为五进制数. 解:由1011001(2)=1×25+1×24+0×23+0×22
+1×21+1×25 = 89 89 = 5×17+4
17 = 5×3+2
3 = 5×0+3思考: 如何把二进制数1011001化为五进制数. 分析:要在非十进制之间实现转化,一个自然
的想法是利用十进制作桥梁.先将二进制数转化为
十进制数,在将十进制数转化为五进制数. 解:所以 89 = 324(5)即 1011001(2) = 324(5)注意: 任意两种进位制的数之间的转化方法:先
将“k进制转十进制”,再将“十进制转s进制”。练习:完成下面进位制之间的转化 (1)10212(3) = ___(10);(2)412(5) = ___(7);(3)2376(8) = ___(10);(4)119(10) = ___(6);答案:(2)212(7) (4)315(6) (3)1278(1)104
再依次指出表格中哪些行有你的生日,便知道你的
生月生日. “猜生月生日游戏” “猜生月生日游戏” 这个游戏中用到的“生月生日表”的制作原理是
二进制记数法,它需要掌握“十进制转二进制”的方
法;计算生月生日的程序的算理是“二进制转十进
制”的算理. 进位制是人们为了计数和运算方便而约定的记
数系统,约定满二进一,就是二进制;满十进一,
就是十进制;满十二进一,就是十二进制;满六十
进一,就是六十进制;等等. 即“满几进一”就是几
进制,几进制的基数(都是大于1的整数)就是几. 十进制数3721中的3表示3个千,7表示7个百,2表示2个十,1表示1个一,于是可得下面的式子: 与十进制类似,其他的进位制也可以按照位置原则计数,如:110011(2)= 7342(8)= 3721=3×103+7×102+2×101+1×1001×25+1×24+0×23+0×22+1×21
+1×25 7×83+3×82+4×81+2×80 一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式.anan-1··· a1a0(k)(0
的幂的乘机之和的形式,再按照十进制数的运算
规则计算出结果.解:110011(2)=1×25+1×24+0×23+0×22
+1×21+1×25 = 1×32+1×16+1×2+1= 51练习:将下面两个非十进制数分别转化为十进制
数.(1)101001(2)(2)324(5)答案:(1)81,(2)89思考:体会“二进制转十进制”的算理,你能否设计
一个算法,把其他进位制数化为十进制数?问题:设计一个算法,把k进制数a(共有n位)化为十
进制数b. 算法分析: 从计算过程可以看出,计算k进制数a的右数
第i位数字ai与ki-1的乘积ai·ki-1,再将其累加,这
是一个重复操作的步骤,所以,可以用循环结构
来构造算法.问题:设计一个算法,把k进制数a(共有n位)化为十
进制数b. 算法步骤:
第一步,输入a,k和n的值. 第二步,将b的值初始化为0,将i的值初始化
为1.第五步,输出b的值.第三步,b=b+ai·ki-1,i=i+1. 第四步,判断i>n.若是,则执行第五步;否
则,返回第三步.程序框图: 下面我们以3721为例,探究“除10取余”的过
程: 3721=372×10+1, 372=37×10+2, 37=3×10+7, 3=0×10+3。 所以3721=10×(10×(10×3+7)+2)+1 =3×103+7×102+2×101+1×100 下面给出 “除10取余”的十进制记数法则:一个十进制数a除以10所得的商是b0,余数是a0 , 即 a=b0×10+a0,
则a0是a的个位数;
b0除以10所得的商是b1,余数是a1,
即 b0=b1×10+a1,
则a1是a的十位数.
…
一般地,bn-1除以10所得的商是bn,余数是an,
即 bn-1=bn×10+an,
则an是a的从右往左数第n+1位数. “除2取余”的二进制记数法则:一个十进制数a除以2所得的商是b0,余数是a0 , 即 a=b0×2+a0,
则a0是a的右边第一位数;
b0除以2所得的商是b1,余数是a1,
即 b0=b1×2+a1,
则a1是a的右边第二位数.
…
一般地,bn-1除以2所得的商是bn,余数是an,
即 bn-1=bn×2+an,
则an是a的从右往左数第n+1位数. 再将依次得到的余数从右到左排列,就可得
到这个2进制数. 上述方法可以推广为把十进制数转化为k进
制数的算法,称为除k取余法.思考:你能将上述算理 推广到“十进制转k进制”
吗?请写出算法步骤、程序框图和程序.算法分析: 一个十进制数a除以k所得的商是q0,余数是
r0,即:
a=q0×k+r0,
则r0是a的k进制数的右数第一位数;
若q0除以k所得的商是q1,余数是r1,即:
a=q1×k+r1,
则r1是a的k进制数的右数第二位数.
…
若qn-1除以k所得的商是0,余数是rn,即qn-1=rn,
则是a的k进制数的左数第一位数. 算法步骤:
第一步,给定十进制正整数a和转化后的数的
基数k. 第二步,求出a除以k所得的商q,余数r. 第三步,若q≠0,则a=q,返回第二步;否
则,执行第四步. 第四步,将依次得到的余数从右到走排列,
得到k进制数.程序框图:请以十进制数89为例,探究“除2取余”的过程.计算方法:89=44×2+1,
44=22×2+0, 22=11×2+0,
11=5×2+1 , 5=2×2+1,
2=1×2+0 , 1=0×2+1
所以
89=2×(2×(2×(2×(2×2+1)
+1)+0)+0)+1
=1×26+0×25+1×24+1×23
+0×23+0×21+1×20
=1011001(2)思考:你能给出“除2取余”的二进制记数法则吗? 这种算法叫做除2取余法练习:
(1)用“除k取余法”将十进制数2008转化为五进
制数和八进制数.(2)把389化成四进制数的末位为( )(A) 1 (B) 2 (C) 3 (D) 0 A 答案:31013(5),3730(8) 思考: 如何把二进制数1011001化为五进制数. 分析:要在非十进制之间实现转化,一个自然
的想法是利用十进制作桥梁.先将二进制数转化为
十进制数,在将十进制数转化为五进制数. 解:由1011001(2)=1×25+1×24+0×23+0×22
+1×21+1×25 = 89 89 = 5×17+4
17 = 5×3+2
3 = 5×0+3思考: 如何把二进制数1011001化为五进制数. 分析:要在非十进制之间实现转化,一个自然
的想法是利用十进制作桥梁.先将二进制数转化为
十进制数,在将十进制数转化为五进制数. 解:所以 89 = 324(5)即 1011001(2) = 324(5)注意: 任意两种进位制的数之间的转化方法:先
将“k进制转十进制”,再将“十进制转s进制”。练习:完成下面进位制之间的转化 (1)10212(3) = ___(10);(2)412(5) = ___(7);(3)2376(8) = ___(10);(4)119(10) = ___(6);答案:(2)212(7) (4)315(6) (3)1278(1)104
