1.2 任意的三角函数---三角函数线
文档属性
| 名称 | 1.2 任意的三角函数---三角函数线 |  | |
| 格式 | zip | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-12 20:57:27 | ||
图片预览





文档简介
课件13张PPT。引言:角是一个几何概念,同时角的大小也具有数量特征.我们从数的观点定义了三角函数,如果能从图形上找出三角函数的几何意义,就能实现数与形的完美统一. 任意角的三角函数(三)
三角函数线口诀:一全正,二正弦,三正切,四余弦.2、诱导公式( )即:终边相同的角的同名三角函数值相等1、三角函数的正负复习回顾知识探究(一):正弦线和余弦线 思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则
, 都是正数,你能分别用一条线段表示角α的正弦值和余弦值吗?思考2:若角α为第三象限角,其终边与单位圆的交点为P(x,y),则
都是负数,此时角α的正弦值和余弦值分别用哪条线段表示?规定:1.OM看作O为起点,M为终点的有向线段。
2.线段的方向与相应坐标轴
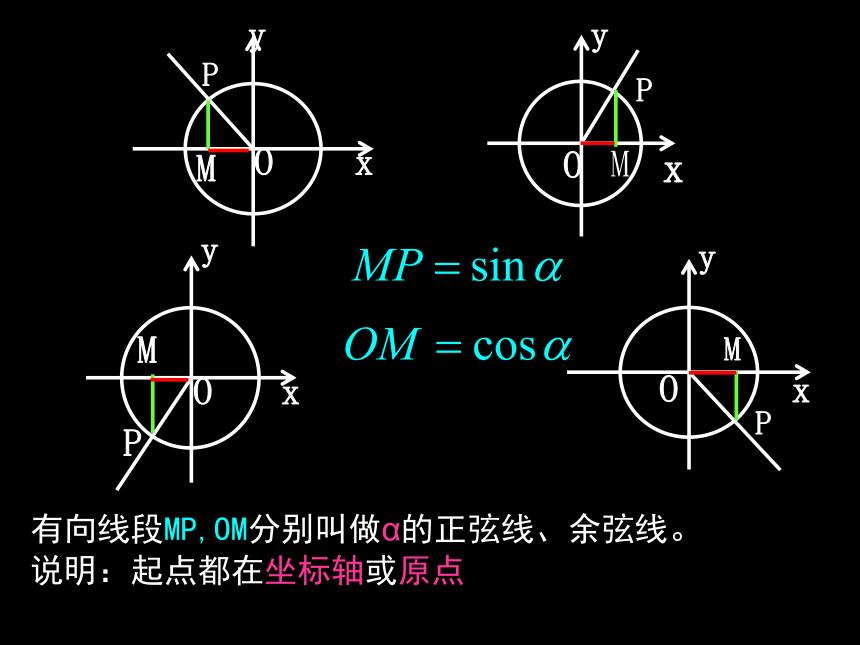
同向时为正方向,反向时为负方向. 有向线段MP,OM分别叫做α的正弦线、余弦线。
说明:起点都在坐标轴或原点POxyPOxyMP例1:设α为锐角,你能根据正弦线和余弦线说明sinα+cosα>1吗?MP+OM>OP=1知识探究(二):正切线 思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则 是正数,用哪条有向线段表示角α的正切值最合适?规定:有向线段AT叫做角α的正切线。
正切线、正弦线、余弦线统称为三角函数线。反思:当角α的终边在坐标轴上时,角α的正切线的含义如何?当角α的终边在x轴上时,角α的正切线是一个点;当角α的终边在y轴上时,角α的正切线不存在.例2:观察下列不等式:
你有什么一般猜想?怎么证明? (其中α为锐角)例3.作出下列各角的正弦线、余弦线、正切线: (1) ; (2) ;
例4.在0~ 内,求使 成立的α的取值范围.思考题:求函数 的定义域.1.三角函数线的定义,及三角函数的方向规定2.利用三角函数线比较大小3.利用三角函数线解三角不等式总结反思作业:
《三维设计》P11页——第9、10题
三角函数线口诀:一全正,二正弦,三正切,四余弦.2、诱导公式( )即:终边相同的角的同名三角函数值相等1、三角函数的正负复习回顾知识探究(一):正弦线和余弦线 思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则
, 都是正数,你能分别用一条线段表示角α的正弦值和余弦值吗?思考2:若角α为第三象限角,其终边与单位圆的交点为P(x,y),则
都是负数,此时角α的正弦值和余弦值分别用哪条线段表示?规定:1.OM看作O为起点,M为终点的有向线段。
2.线段的方向与相应坐标轴
同向时为正方向,反向时为负方向. 有向线段MP,OM分别叫做α的正弦线、余弦线。
说明:起点都在坐标轴或原点POxyPOxyMP例1:设α为锐角,你能根据正弦线和余弦线说明sinα+cosα>1吗?MP+OM>OP=1知识探究(二):正切线 思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则 是正数,用哪条有向线段表示角α的正切值最合适?规定:有向线段AT叫做角α的正切线。
正切线、正弦线、余弦线统称为三角函数线。反思:当角α的终边在坐标轴上时,角α的正切线的含义如何?当角α的终边在x轴上时,角α的正切线是一个点;当角α的终边在y轴上时,角α的正切线不存在.例2:观察下列不等式:
你有什么一般猜想?怎么证明? (其中α为锐角)例3.作出下列各角的正弦线、余弦线、正切线: (1) ; (2) ;
例4.在0~ 内,求使 成立的α的取值范围.思考题:求函数 的定义域.1.三角函数线的定义,及三角函数的方向规定2.利用三角函数线比较大小3.利用三角函数线解三角不等式总结反思作业:
《三维设计》P11页——第9、10题
