1.2.1(2)任意角的三角函数(二)
文档属性
| 名称 | 1.2.1(2)任意角的三角函数(二) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-13 18:14:47 | ||
图片预览





文档简介
(共16张PPT)
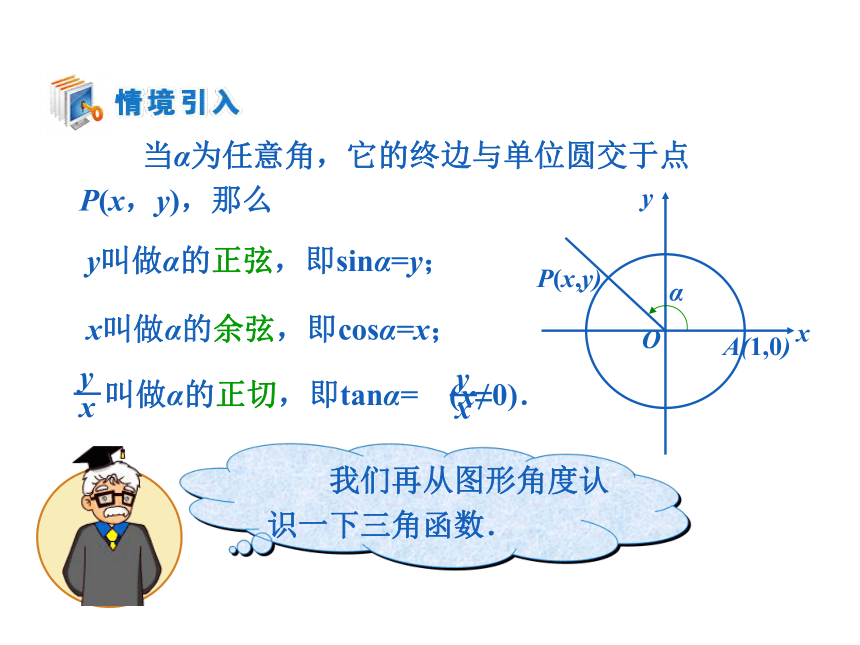
任意角的三角函数
当α为任意角,它的终边与单位圆交于点
P(x,y),那么
y叫做α的正弦,即sinα=y;
x叫做α的余弦,即cosα=x;
叫做α的正切,即tanα= (x≠0).
y
x
y
x
x
O
y
A(1,0)
P(x,y)
α
我们再从图形角度认识一下三角函数.
我们也能用线段来表示三角函数
|sinα|=|y|=|MP|
|cosα|=|x|=|OM|
我们知道,直角坐标系内点的坐标与坐标轴的方向有关.因此,可以用坐标轴的方向来规定线段OM、MP的方向,使他们的取值与P点的坐标联系起来.
你能想个办法去掉等式中的绝对值符号,使它们的取值与点P的坐标一致吗?
当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有负值x.其中x为P点的横坐标.这样,无论哪一种情况都有
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
OM=x=cosα.
当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y.其中y为P点的纵坐标.这样,无论哪一种情况都有
同理,当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:
MP=y=sinα.
像OM、MP这种被看作带有方向的线段,叫做有向线段(directed line segment).
你能用有向线段来表示正切吗?
例:作出角 的正弦线、余弦线和正切线,并求出它的正弦、余弦和正切的值.
5π
4
M
T
A(1,0)
x
O
y
P(x,y)
5π
4
解:如图,MP为正弦线,
OM为余弦线,
TA为正切线.
5π
4
sin =-
√2
2
5π
4
cos =-
√2
2
5π
4
tan =1
A(1,0)
x
O
y
P(x,y)
2π
3
-
1.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.
2π
3
-
(1)
13π
6
-
(2)
M
T
解:(1)如图,MP为正弦线, OM为余弦线, TA为正切线.
2π
3
-
sin =-
√3
2
2π
3
-
cos =-
1
2
2π
3
-
tan =-√3
1.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.
2π
3
-
(1)
13π
6
-
(2)
(2)如图,MP为正弦线, OM为余弦线, TA为正切线.
M
T
A(1,0)
x
O
y
P(x,y)
sin =-
13π
6
-
1
2
√3
2
cos =
13π
6
-
√3
3
tan =-
13π
6
-
②
2.设MP和OM分别是角 的正弦线和余弦线,则给出的以下不等式:
17π
18
① MP<OM<0;
② OM<0<MP;
③ OM<MP<0;
④ MP<0<OM.
其中正确的是________.
x
O
y
P(x,y)
M
17π
18
A(1,0)
证明:由图可知:sinα=MP,cosα=OM,OP=1.
又由三角形的任意两边之和大于第三边知:
MP+OM>OP,
3.当0<α< 时,证明: sinα+cosα>1.
π
2
所以 sinα+cosα>1.
x
O
y
P
M
A(1,0)
α
求证:当α为锐角时,sinα<α<tanα.
分析:sinα,tanα都是三角比值,是实数,而当α用弧度制表示时,它的弧度数也是一个实数,因此这三个实数可比较大小.另外,可把这三个实数转化为线的大小、面积的大小来比较.
证明:如图,作单位圆,当0<α< 时作出正弦线MP和正切线AT,连接PA.
π
2
x
O
y
P
M
A(1,0)
α
T
x
O
y
P
M
A(1,0)
α
T
∴ |OA|=1,|AP|=|OA|·α=α,OM=sinα,AT=tanα
⌒
∵ S△OPA<S扇形OPA<S△OAT
∴ |OA|×|MP|< |OA|×|AP|< |OA|×|AT|
1
2
1
2
1
2
⌒
∴ |MP|<|AP|<|AT|
⌒
∴ sinα<α<tanα.
任意角的三角函数
当α为任意角,它的终边与单位圆交于点
P(x,y),那么
y叫做α的正弦,即sinα=y;
x叫做α的余弦,即cosα=x;
叫做α的正切,即tanα= (x≠0).
y
x
y
x
x
O
y
A(1,0)
P(x,y)
α
我们再从图形角度认识一下三角函数.
我们也能用线段来表示三角函数
|sinα|=|y|=|MP|
|cosα|=|x|=|OM|
我们知道,直角坐标系内点的坐标与坐标轴的方向有关.因此,可以用坐标轴的方向来规定线段OM、MP的方向,使他们的取值与P点的坐标联系起来.
你能想个办法去掉等式中的绝对值符号,使它们的取值与点P的坐标一致吗?
当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有负值x.其中x为P点的横坐标.这样,无论哪一种情况都有
当角α的终边不在坐标轴上时,以O为始点、M为终点,规定:
OM=x=cosα.
当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y.其中y为P点的纵坐标.这样,无论哪一种情况都有
同理,当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:
MP=y=sinα.
像OM、MP这种被看作带有方向的线段,叫做有向线段(directed line segment).
你能用有向线段来表示正切吗?
例:作出角 的正弦线、余弦线和正切线,并求出它的正弦、余弦和正切的值.
5π
4
M
T
A(1,0)
x
O
y
P(x,y)
5π
4
解:如图,MP为正弦线,
OM为余弦线,
TA为正切线.
5π
4
sin =-
√2
2
5π
4
cos =-
√2
2
5π
4
tan =1
A(1,0)
x
O
y
P(x,y)
2π
3
-
1.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.
2π
3
-
(1)
13π
6
-
(2)
M
T
解:(1)如图,MP为正弦线, OM为余弦线, TA为正切线.
2π
3
-
sin =-
√3
2
2π
3
-
cos =-
1
2
2π
3
-
tan =-√3
1.作出下列各角的正弦线、余弦线和正切线,并求出它们的正弦、余弦和正切的值.
2π
3
-
(1)
13π
6
-
(2)
(2)如图,MP为正弦线, OM为余弦线, TA为正切线.
M
T
A(1,0)
x
O
y
P(x,y)
sin =-
13π
6
-
1
2
√3
2
cos =
13π
6
-
√3
3
tan =-
13π
6
-
②
2.设MP和OM分别是角 的正弦线和余弦线,则给出的以下不等式:
17π
18
① MP<OM<0;
② OM<0<MP;
③ OM<MP<0;
④ MP<0<OM.
其中正确的是________.
x
O
y
P(x,y)
M
17π
18
A(1,0)
证明:由图可知:sinα=MP,cosα=OM,OP=1.
又由三角形的任意两边之和大于第三边知:
MP+OM>OP,
3.当0<α< 时,证明: sinα+cosα>1.
π
2
所以 sinα+cosα>1.
x
O
y
P
M
A(1,0)
α
求证:当α为锐角时,sinα<α<tanα.
分析:sinα,tanα都是三角比值,是实数,而当α用弧度制表示时,它的弧度数也是一个实数,因此这三个实数可比较大小.另外,可把这三个实数转化为线的大小、面积的大小来比较.
证明:如图,作单位圆,当0<α< 时作出正弦线MP和正切线AT,连接PA.
π
2
x
O
y
P
M
A(1,0)
α
T
x
O
y
P
M
A(1,0)
α
T
∴ |OA|=1,|AP|=|OA|·α=α,OM=sinα,AT=tanα
⌒
∵ S△OPA<S扇形OPA<S△OAT
∴ |OA|×|MP|< |OA|×|AP|< |OA|×|AT|
1
2
1
2
1
2
⌒
∴ |MP|<|AP|<|AT|
⌒
∴ sinα<α<tanα.
