1.4.2三角函数的周期性
图片预览






文档简介
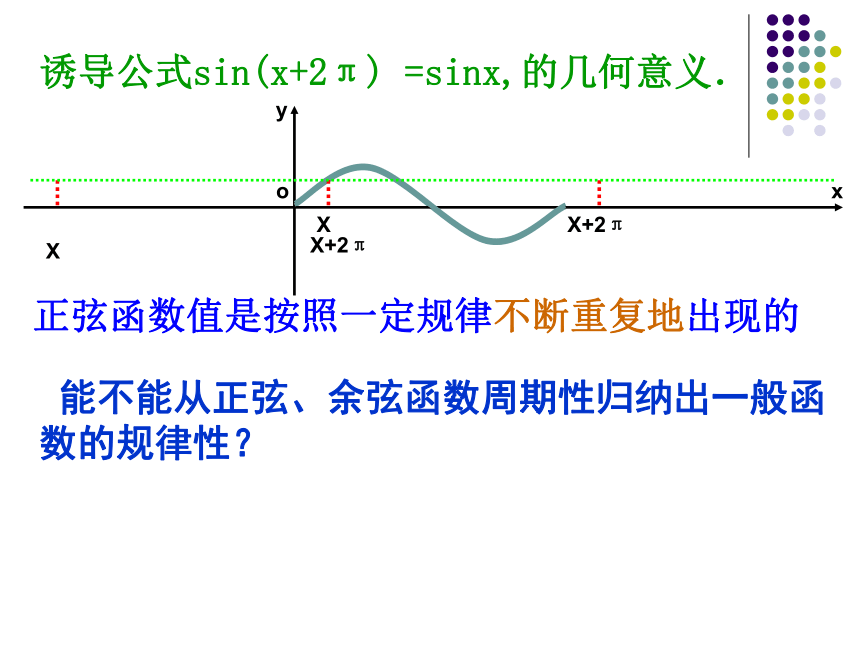
课件18张PPT。1.4.2正弦余弦函数的性质--------周期性1.创设情景,引入课题情景①诱导公式sin(x+2π) =sinx,的几何意义.XX+2πXX+2π正弦函数值是按照一定规律不断重复地出现的 能不能从正弦、余弦函数周期性归纳出一般函数的规律性?1.一般地,对于函数f(x),如果存在一个非零的常数T,使得定义域内的每一个x的值,都满足f(x+T)=f(x),那么函数f(x)就叫做周期函数
非零常数T叫做这个函数的周期
2.对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。?思考:一个周期函数的周期有多少个??正弦函数和余弦函数的最小正周期都是2π.概念?判断下列说法是否正确√× XX+2π自变量x增加2π时函数值不断重复地出现的4π8π6π12π三角函数的周期性:4.T是f(x)的周期,那么kT也一定是f(x)的周期.
(k为非零整数)解(1)是以2π为周期的周期函数.的周期为π. (3)的周期为4π另法解(2)归纳总结练习1.求下列函数的周期:2、求下列函数的周期 一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:周期求法:1.定义法:
2.公式法:3.图象法:小结2.一个函数是周期函数,但它不一定有最小正
周期.例如,f(x)=a(常数) 3.设T是f(x)(x∈R)的周期,那么kT(k∈Z,
且k≠0)也一定是f(x)的周期.1.理解周期定义时要注意,式子f(x+T)=f(x)
是对“x”而言. 5.y=|sinx|及y=|cosx|的周期为π2. 是不是周期函数?为什么?1.y=sinx(x∈[0,4π])是周期函数吗?作业:P36 2
非零常数T叫做这个函数的周期
2.对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期。?思考:一个周期函数的周期有多少个??正弦函数和余弦函数的最小正周期都是2π.概念?判断下列说法是否正确√× XX+2π自变量x增加2π时函数值不断重复地出现的4π8π6π12π三角函数的周期性:4.T是f(x)的周期,那么kT也一定是f(x)的周期.
(k为非零整数)解(1)是以2π为周期的周期函数.的周期为π. (3)的周期为4π另法解(2)归纳总结练习1.求下列函数的周期:2、求下列函数的周期 一般地,函数 y=Asin(ωx+φ) 及y=Acos(ωx+φ) (其中A ,ω,φ为常数,且 A≠0, ω≠0 )的周期是:周期求法:1.定义法:
2.公式法:3.图象法:小结2.一个函数是周期函数,但它不一定有最小正
周期.例如,f(x)=a(常数) 3.设T是f(x)(x∈R)的周期,那么kT(k∈Z,
且k≠0)也一定是f(x)的周期.1.理解周期定义时要注意,式子f(x+T)=f(x)
是对“x”而言. 5.y=|sinx|及y=|cosx|的周期为π2. 是不是周期函数?为什么?1.y=sinx(x∈[0,4π])是周期函数吗?作业:P36 2
