2.3 平面向量的基本定理及坐标表示
文档属性
| 名称 | 2.3 平面向量的基本定理及坐标表示 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-13 18:17:00 | ||
图片预览






文档简介
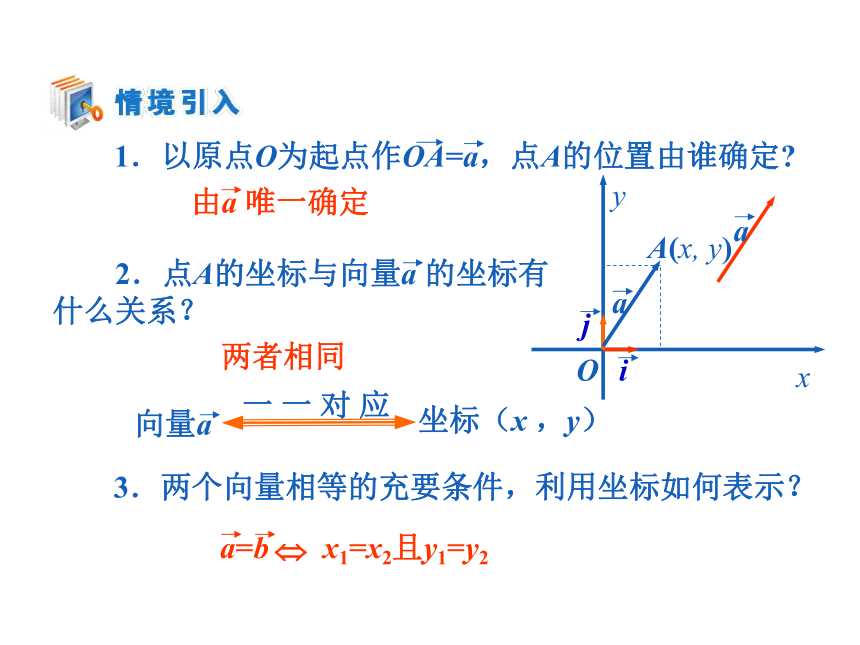
课件19张PPT。两者相同3.两个向量相等的充要条件,利用坐标如何表示?=(x2,y2)-(x1- y1)=(x2-x1,y2 -y1)解:=(6,3)+(-12,16)=(-6,19). 例3 如图,已知平行四边形ABCD的三个顶点A、B、C的坐标分别是(-2,1)、(-1,3) 、(3,4),试求顶点D的坐标. 解法1:设顶点D的坐标为(x,y).(1,2)=(3-x,4-y) .∴顶点D的坐标为(2,2). 解法2:如图,由向量加法的平行四边形法则可知∴顶点D的坐标为(2,2).=(-2-(-1),1-3)+(3-(-1),4-3)=(2,2).=(-1,3)+(3,-1)=(3,-1),(x1,y1)=λ(x2,y2)即消去λ后得: x1y2-x2y1=0. 这就是说,当且仅当x1y2-x2y1=0∴ 4y-2×6=0. ∴ y=3. 例5 已知A(-1,-1)、 B(1,3)、C(2,5),试判断A、 B、C三点之间的位置关系. 解:在平面直角坐标系中作出A、 B、C三点(如下图),观察图形,猜想A、 B、C三点共线.又 2×6-3×4=0. ∵ 直线AB、直线AC有公共点A,∴ A、 B、C三点共线. 例6 设点P是线段P1P2上的一点,P1、P2的坐标分别是(x1,y1)、(x2,y2). (1)当点P是线段P1P2的中点时,求点P的坐标; 解:如图,由向量的线性运算可知 (2)当点P是线段P1P2的一个三等分点时,求点P的坐标. (2)当点P是线段P1P2的一个三等分点时,求点P的坐标.点P的坐标是: 练习2.已知平行四边形ABCD的顶点A(-1,-2)、 B(3,-1)、C(5,6),求顶点D的坐标.顶点D的坐标为(1,5).所以解得 x=-4. 如果存在,求出x、y、z的值;如果不存在,说明理由.(2,3)=x(3,1)+y(2,2)+z(-1,5)=(3x+2y-z,x+2y+5z).则消z得方程组显然无解,所以不存在这样的实数x、y、z.
