6.2.1 向量的加法运算-高中数学人教A版(2019)必修二 课件(共30张PPT)
文档属性
| 名称 | 6.2.1 向量的加法运算-高中数学人教A版(2019)必修二 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 18:33:32 | ||
图片预览







文档简介
(共30张PPT)
向量的加法运算
1.理解向量加法的概念以及向量加法的几何意义.
2.掌握向量加法的平行四边形法则和三角形法则,会用它们
解决实际问题.
3.掌握向量加法的交换律和结合律,会用它们进行计算.
向量加法的三角形法则
1
那么向量的加法是怎样定义的?
长度是1 的向量与长度是2的向量相加是否一定是长度为3的向量呢?
数可进行加法运算:
1+2=3
两个向量相加,就是两个向量的模相加吗?
提示:不是.模相加是数量的加法.
物理背景位移、力
问题一
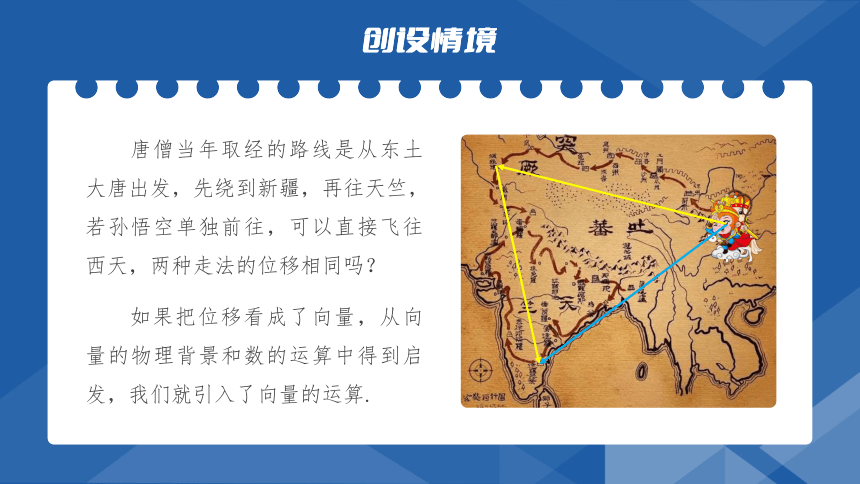
唐僧当年取经的路线是从东土大唐出发,先绕到新疆,再往天竺,若孙悟空单独前往,可以直接飞往西天,两种走法的位移相同吗?
如果把位移看成了向量,从向量的物理背景和数的运算中得到启发,我们就引入了向量的运算.
知识梳理
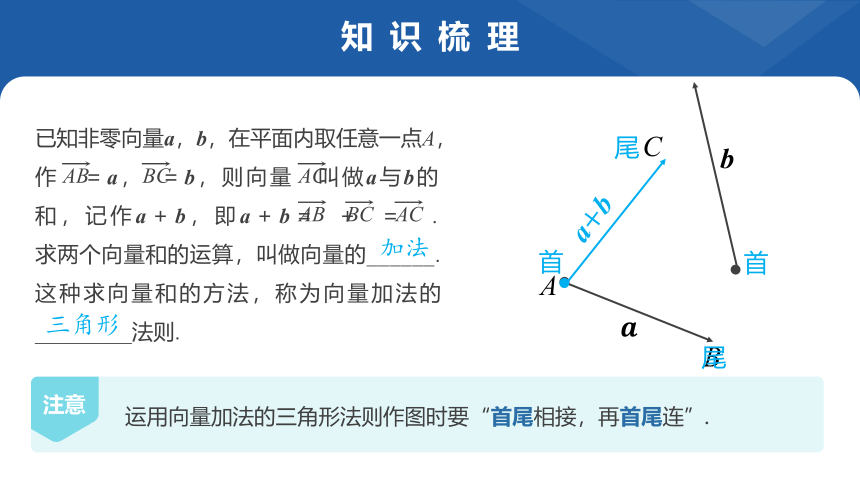
已知非零向量a,b,在平面内取任意一点A,作 =a, =b,则向量 叫做a与b的
和,记作a+b,即a+b= + = .
求两个向量和的运算,叫做向量的______.
这种求向量和的方法,称为向量加法的_________法则.
加法
三角形
AB
BC
AC
AB
BC
AC
.
.
ab
A
B
C
尾
首
首
尾
.
b
运用向量加法的三角形法则作图时要“首尾相接,再首尾连”.
注意
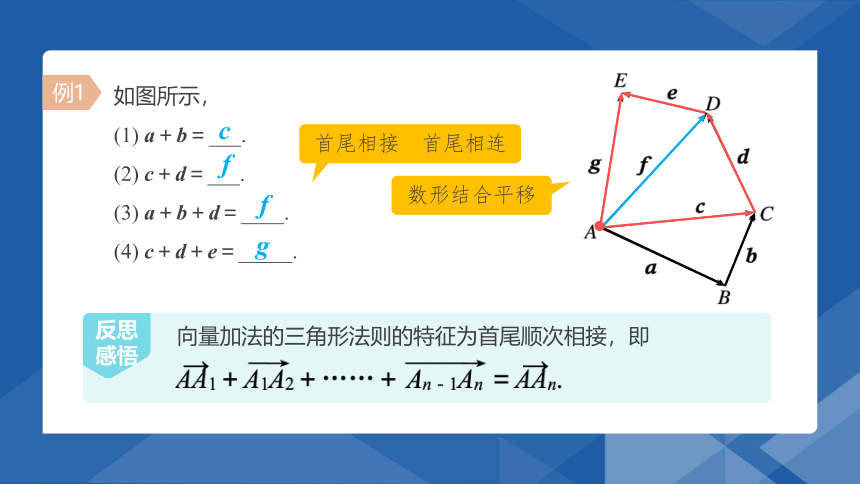
如图所示,
(1) a+b=___.
(2) c+d=___.
(3) a+b+d=____.
(4) c+d+e=_____.
c
f
f
g
.
例1
首尾相接 首尾相连
数形结合平移
向量加法的三角形法则的特征为首尾顺次相接,即
反思感悟
向量加法的平行四边形法则
2
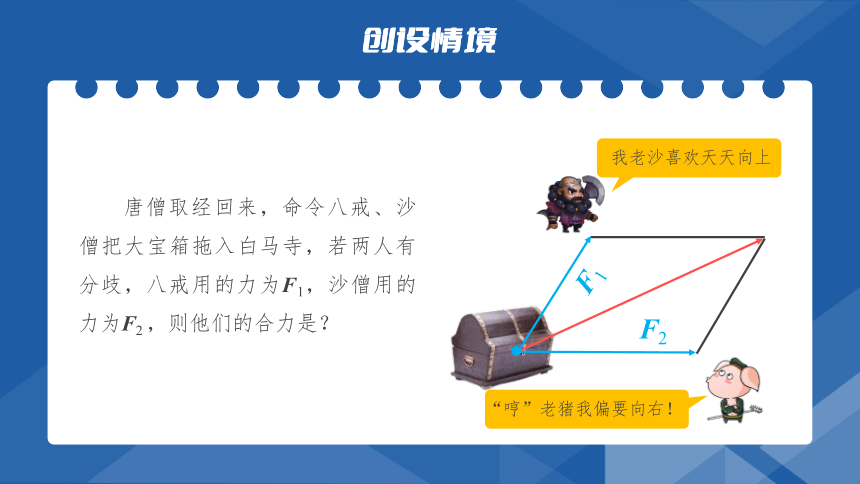
唐僧取经回来,命令八戒、沙僧把大宝箱拖入白马寺,若两人有分歧,八戒用的力为F1,沙僧用的力为F2 ,则他们的合力是?
F2
F1
.
“哼”老猪我偏要向右!
我老沙喜欢天天向上
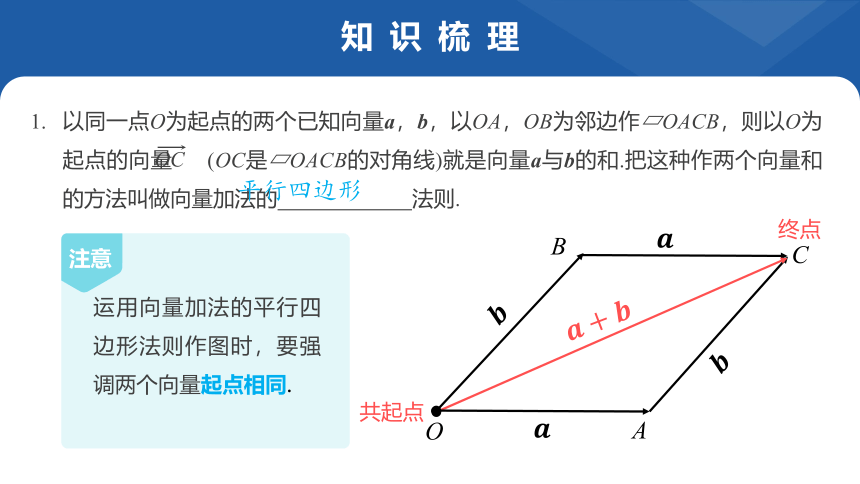
以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量 (OC是 OACB的对角线)就是向量a与b的和.把这种作两个向量和的方法叫做向量加法的 法则.
知识梳理
OC
运用向量加法的平行四边形法则作图时,要强调两个向量起点相同.
注意
平行四边形
C
终点
共起点
O
A
B
.
.
知识梳理
一致
从平行四边形的性质可知三角形法则和平行四边形法则是 的.
对于零向量与任意向量a,规定a+0=0+a=____.
a
①向量加法的平行四边形法则不适用与两个向量共线的情况.
②向量加法的三角形法则任何情况都适用.
注意
.
.
.
.
.
.
例2
如图,已知向量a,b,c,求作和向量a+b+c.
解 方法一 可先作a+c,再作(a+c)+b,即a+b+c.如图:
.
O
A
.
.
B
C
例2
如图,已知向量a,b,c,求作和向量a+b+c.
解 方法二 三个向量不共线,用平行四边形法则来作.如图:
.
O
A
.
.
B
C
D
E
反思感悟
平移向量使之“首尾相接”,即第一个向量的终点与第二个向量的起点重合.
以第一个向量的起点为起点,并以第二个向量的终点为终点的向量,即为两个向量的和.
平移两个不共线的向量使之共起点.
以这两个已知向量为邻边作平行四边形.
平行四边形中,与两向量共起点的对角线表示的向量为两个向量的和.
应用三角形法则求向量和的基本步骤
应用平行四边形法则求向量和的基本步骤
如图,已知向量a,b,求作向量a+b.
跟踪训练1
共线向量的加法与
向量加法的运算律
3
提示:两个向量相加仍是一个向量,两个数相加是一个数量.能.
如果向量a,b共线,它们的加法与数的加法有什么关系?你能做出向量a+b吗?
问题二
知识梳理
一般地,我们有|a+b|≤ ,当且仅当a,b方向 时等号成立.
(加法交换律)a+b=b+a;
(加法结合律)a+(b+c)= .
相同
|a|+|b|
(a+b)+c
.
.
.
.
.
例3
设A,B,C,D是平面上的任意四点,试化简:
反思感悟
向量加法运算律的意义和应用原则
意义
向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
应用原则
利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:
跟踪训练2
向量加法的实际应用
4
例4
解 如图,
.
例4
解
.
反思感悟
应用向量解决平面几何和物理学问题的基本步骤
表示
用向量表示有关量,将所要解答的问题转化为向量问题.
运算
应用向量加法的平行四边形法则和三角形法则,将相关向量进行运算,解答向量问题.
还原
根据向量的运算结果,结合向量共线、相等等概念回答原问题.
如图所示,在某次抗震救灾中,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
跟踪训练3
又α=35°,β=55°,∠ABC=35°+55°=90°,
课堂小结
1. 知识清单:
(1)向量加法的三角形法则
(2)向量加法的平行四边形法则
(3)向量三角不等式
(4)向量加法的运算律
2. 方法归纳:数形结合.
3. 常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
向量的加法运算
1.理解向量加法的概念以及向量加法的几何意义.
2.掌握向量加法的平行四边形法则和三角形法则,会用它们
解决实际问题.
3.掌握向量加法的交换律和结合律,会用它们进行计算.
向量加法的三角形法则
1
那么向量的加法是怎样定义的?
长度是1 的向量与长度是2的向量相加是否一定是长度为3的向量呢?
数可进行加法运算:
1+2=3
两个向量相加,就是两个向量的模相加吗?
提示:不是.模相加是数量的加法.
物理背景位移、力
问题一
唐僧当年取经的路线是从东土大唐出发,先绕到新疆,再往天竺,若孙悟空单独前往,可以直接飞往西天,两种走法的位移相同吗?
如果把位移看成了向量,从向量的物理背景和数的运算中得到启发,我们就引入了向量的运算.
知识梳理
已知非零向量a,b,在平面内取任意一点A,作 =a, =b,则向量 叫做a与b的
和,记作a+b,即a+b= + = .
求两个向量和的运算,叫做向量的______.
这种求向量和的方法,称为向量加法的_________法则.
加法
三角形
AB
BC
AC
AB
BC
AC
.
.
ab
A
B
C
尾
首
首
尾
.
b
运用向量加法的三角形法则作图时要“首尾相接,再首尾连”.
注意
如图所示,
(1) a+b=___.
(2) c+d=___.
(3) a+b+d=____.
(4) c+d+e=_____.
c
f
f
g
.
例1
首尾相接 首尾相连
数形结合平移
向量加法的三角形法则的特征为首尾顺次相接,即
反思感悟
向量加法的平行四边形法则
2
唐僧取经回来,命令八戒、沙僧把大宝箱拖入白马寺,若两人有分歧,八戒用的力为F1,沙僧用的力为F2 ,则他们的合力是?
F2
F1
.
“哼”老猪我偏要向右!
我老沙喜欢天天向上
以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量 (OC是 OACB的对角线)就是向量a与b的和.把这种作两个向量和的方法叫做向量加法的 法则.
知识梳理
OC
运用向量加法的平行四边形法则作图时,要强调两个向量起点相同.
注意
平行四边形
C
终点
共起点
O
A
B
.
.
知识梳理
一致
从平行四边形的性质可知三角形法则和平行四边形法则是 的.
对于零向量与任意向量a,规定a+0=0+a=____.
a
①向量加法的平行四边形法则不适用与两个向量共线的情况.
②向量加法的三角形法则任何情况都适用.
注意
.
.
.
.
.
.
例2
如图,已知向量a,b,c,求作和向量a+b+c.
解 方法一 可先作a+c,再作(a+c)+b,即a+b+c.如图:
.
O
A
.
.
B
C
例2
如图,已知向量a,b,c,求作和向量a+b+c.
解 方法二 三个向量不共线,用平行四边形法则来作.如图:
.
O
A
.
.
B
C
D
E
反思感悟
平移向量使之“首尾相接”,即第一个向量的终点与第二个向量的起点重合.
以第一个向量的起点为起点,并以第二个向量的终点为终点的向量,即为两个向量的和.
平移两个不共线的向量使之共起点.
以这两个已知向量为邻边作平行四边形.
平行四边形中,与两向量共起点的对角线表示的向量为两个向量的和.
应用三角形法则求向量和的基本步骤
应用平行四边形法则求向量和的基本步骤
如图,已知向量a,b,求作向量a+b.
跟踪训练1
共线向量的加法与
向量加法的运算律
3
提示:两个向量相加仍是一个向量,两个数相加是一个数量.能.
如果向量a,b共线,它们的加法与数的加法有什么关系?你能做出向量a+b吗?
问题二
知识梳理
一般地,我们有|a+b|≤ ,当且仅当a,b方向 时等号成立.
(加法交换律)a+b=b+a;
(加法结合律)a+(b+c)= .
相同
|a|+|b|
(a+b)+c
.
.
.
.
.
例3
设A,B,C,D是平面上的任意四点,试化简:
反思感悟
向量加法运算律的意义和应用原则
意义
向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
应用原则
利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:
跟踪训练2
向量加法的实际应用
4
例4
解 如图,
.
例4
解
.
反思感悟
应用向量解决平面几何和物理学问题的基本步骤
表示
用向量表示有关量,将所要解答的问题转化为向量问题.
运算
应用向量加法的平行四边形法则和三角形法则,将相关向量进行运算,解答向量问题.
还原
根据向量的运算结果,结合向量共线、相等等概念回答原问题.
如图所示,在某次抗震救灾中,一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
跟踪训练3
又α=35°,β=55°,∠ABC=35°+55°=90°,
课堂小结
1. 知识清单:
(1)向量加法的三角形法则
(2)向量加法的平行四边形法则
(3)向量三角不等式
(4)向量加法的运算律
2. 方法归纳:数形结合.
3. 常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
