6.4.1 平面几何中的向量方法-高中数学人教A版(2019)必修二 课件(共32张PPT)
文档属性
| 名称 | 6.4.1 平面几何中的向量方法-高中数学人教A版(2019)必修二 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
平面几何中的向量方法
1.能用向量方法解决简单的几何问题.
2.体会向量在解决数学问题中的作用.
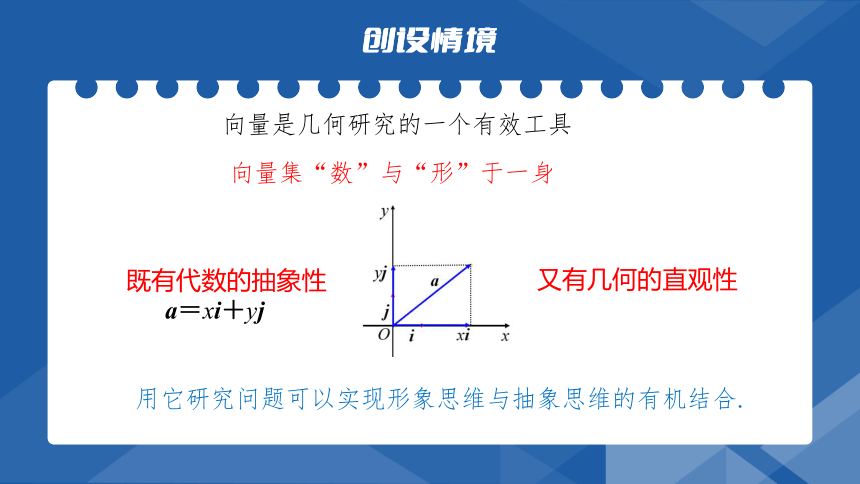
用它研究问题可以实现形象思维与抽象思维的有机结合.
向量集“数”与“形”于一身
既有代数的抽象性
又有几何的直观性
向量是几何研究的一个有效工具
a=xi+yj
用向量解决
平面几何中的平行(或共线)问题
1
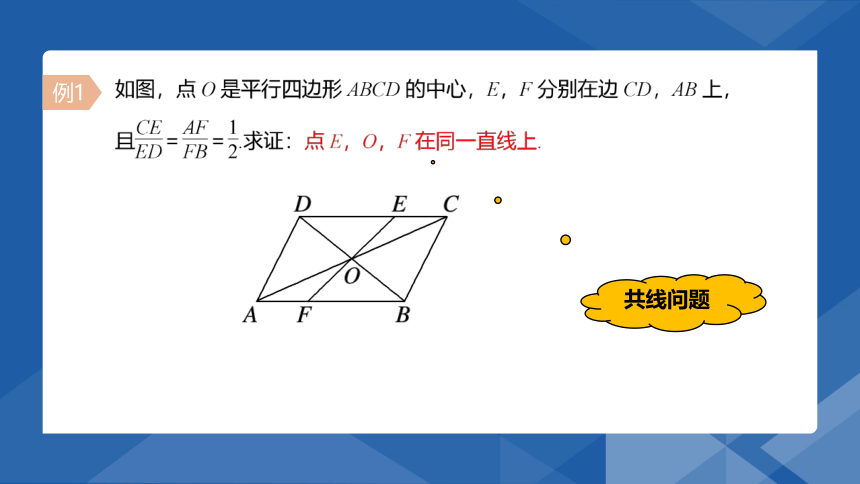
例1
共线问题
例1
知E,F分别是CD,AB的三等分点,
几何问题转向量问题
反思感悟
用向量方法解决平面几何问题的“三步曲”
建立联系
建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
运算
通过向量运算,研究几何元素之间的关系.
翻译
把运算结果“翻译”成几何关系.
设P,Q分别是梯形ABCD的对角线AC与BD的中点,AB∥DC,
试用向量证明:PQ∥AB.
又P,Q,A,B四点不共线,所以PQ∥AB.
跟踪训练1
利用向量证明平面几何问题
2
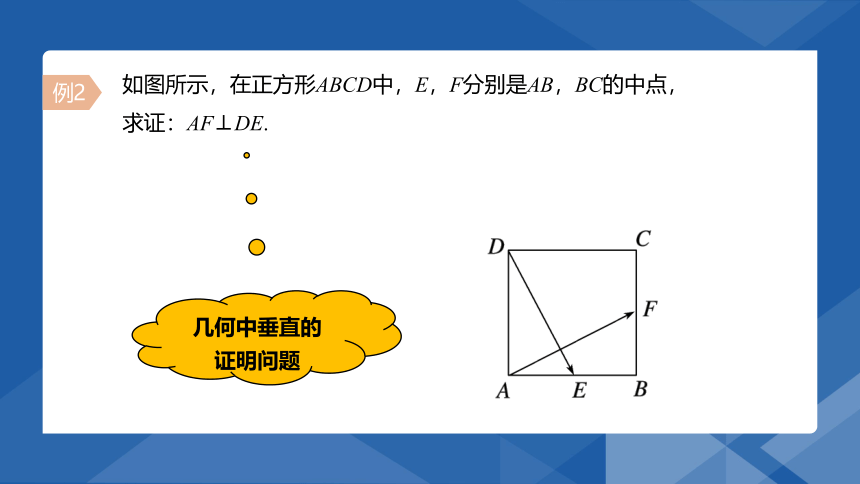
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,
求证:AF⊥DE.
例2
几何中垂直的
证明问题
则|a|=|b|,a·b=0.
向量的线性运算法
例2
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
方法二 如图所示,建立平面直角坐标系,
设正方形的边长为2,
则A(0,0),D(0,2),E(1,0),F(2,1),
向量的坐标运算法
例2
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
反思感悟
用向量证明平面几何问题的两种基本思路
向量的线性运算法
①选取基底;
②用基底表示相关向量;
③利用向量的线性运算或数量积找到相应关系;
④把计算所得结果转化为几何问题.
向量的坐标运算法
①建立适当的平面直角坐标系;
②把相关向量坐标化;
③利用向量的坐标运算找到相应关系;
④利用向量关系回答几何问题.
如图,在正方形ABCD中,P为对角线AC上任一点,PE⊥AB,PF⊥BC,垂足分别为E,F,连接DP,EF,求证:DP⊥EF.
向量的线性运算法
向量的坐标运算法
跟踪训练2
证明 方法一 设正方形ABCD的边长为1,AE=a(0=-a+a2+a(1-a)=0.
跟踪训练2
方法二 如图,以A为原点,AB,AD所在直线分别为x轴,y轴建立平面直角坐标系.
设正方形ABCD的边长为1,AP=λ(0<λ< ),
跟踪训练2
利用平面向量
求几何中的长度问题
3
例3
几何中的
长度问题
在平行四边形ABCD中,AB=2,AD=4,∠BAD=60°,E是BC的中点,F是AE的中点,则向量 的模长是_____.
向量的
数量积转化
反思感悟
用向量法求长度的策略
选基底
根据图形特点选择基底,
利用向量的数量积转化,
用公式|a|2=a2求解.
建立坐标系,
确定相应向量的坐标,
代入公式:若a=(x,y),
则|a|= .
建系
跟踪训练3
利用平面向量
求几何中的角度问题
4
例4
长度问题
例4
角度问题
∴θ=90°,即∠DAC=90°.
向量的夹角公式
反思感悟
用向量法求角度的策略
方法
①将要求的角转化为两向量的夹角;
②再使用基底法或坐标法求出该夹角的余弦值;
③然后求出该夹角;
④再转化为实际问题中的角即可.
注意事项
要注意两向量的夹角和要求角的关系.
45°
跟踪训练4
=-[16×(-21)+12×3]=300,
又∠0°<∠OAB<180°,所以∠OAB=45°.
课堂小结
1. 知识清单:
(1)用向量解决平面几何中的平行(或共线)问题.
(2)利用向量证明平面几何问题.
(3)利用平面向量求几何中的长度.
(4)利用平面向量求几何中的角度.
2. 方法归纳:转化法、数形结合法.
3. 常见误区:
不能将几何问题转化为向量问题.
随堂演练
5
解析
1
2
3
4
√
已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为( )
A.梯形 B.菱形 C.矩形 D.正方形
解析
1
2
3
4
√
解析
1
2
3
4
√
在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为AC的中点,则cos∠BDC等于
如图,建立平面直角坐标系,
则B(0,0),A(0,8),C(6,0),D(3,4),
1
2
3
4
1
解析
平面几何中的向量方法
1.能用向量方法解决简单的几何问题.
2.体会向量在解决数学问题中的作用.
用它研究问题可以实现形象思维与抽象思维的有机结合.
向量集“数”与“形”于一身
既有代数的抽象性
又有几何的直观性
向量是几何研究的一个有效工具
a=xi+yj
用向量解决
平面几何中的平行(或共线)问题
1
例1
共线问题
例1
知E,F分别是CD,AB的三等分点,
几何问题转向量问题
反思感悟
用向量方法解决平面几何问题的“三步曲”
建立联系
建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
运算
通过向量运算,研究几何元素之间的关系.
翻译
把运算结果“翻译”成几何关系.
设P,Q分别是梯形ABCD的对角线AC与BD的中点,AB∥DC,
试用向量证明:PQ∥AB.
又P,Q,A,B四点不共线,所以PQ∥AB.
跟踪训练1
利用向量证明平面几何问题
2
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,
求证:AF⊥DE.
例2
几何中垂直的
证明问题
则|a|=|b|,a·b=0.
向量的线性运算法
例2
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
方法二 如图所示,建立平面直角坐标系,
设正方形的边长为2,
则A(0,0),D(0,2),E(1,0),F(2,1),
向量的坐标运算法
例2
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
反思感悟
用向量证明平面几何问题的两种基本思路
向量的线性运算法
①选取基底;
②用基底表示相关向量;
③利用向量的线性运算或数量积找到相应关系;
④把计算所得结果转化为几何问题.
向量的坐标运算法
①建立适当的平面直角坐标系;
②把相关向量坐标化;
③利用向量的坐标运算找到相应关系;
④利用向量关系回答几何问题.
如图,在正方形ABCD中,P为对角线AC上任一点,PE⊥AB,PF⊥BC,垂足分别为E,F,连接DP,EF,求证:DP⊥EF.
向量的线性运算法
向量的坐标运算法
跟踪训练2
证明 方法一 设正方形ABCD的边长为1,AE=a(0
跟踪训练2
方法二 如图,以A为原点,AB,AD所在直线分别为x轴,y轴建立平面直角坐标系.
设正方形ABCD的边长为1,AP=λ(0<λ< ),
跟踪训练2
利用平面向量
求几何中的长度问题
3
例3
几何中的
长度问题
在平行四边形ABCD中,AB=2,AD=4,∠BAD=60°,E是BC的中点,F是AE的中点,则向量 的模长是_____.
向量的
数量积转化
反思感悟
用向量法求长度的策略
选基底
根据图形特点选择基底,
利用向量的数量积转化,
用公式|a|2=a2求解.
建立坐标系,
确定相应向量的坐标,
代入公式:若a=(x,y),
则|a|= .
建系
跟踪训练3
利用平面向量
求几何中的角度问题
4
例4
长度问题
例4
角度问题
∴θ=90°,即∠DAC=90°.
向量的夹角公式
反思感悟
用向量法求角度的策略
方法
①将要求的角转化为两向量的夹角;
②再使用基底法或坐标法求出该夹角的余弦值;
③然后求出该夹角;
④再转化为实际问题中的角即可.
注意事项
要注意两向量的夹角和要求角的关系.
45°
跟踪训练4
=-[16×(-21)+12×3]=300,
又∠0°<∠OAB<180°,所以∠OAB=45°.
课堂小结
1. 知识清单:
(1)用向量解决平面几何中的平行(或共线)问题.
(2)利用向量证明平面几何问题.
(3)利用平面向量求几何中的长度.
(4)利用平面向量求几何中的角度.
2. 方法归纳:转化法、数形结合法.
3. 常见误区:
不能将几何问题转化为向量问题.
随堂演练
5
解析
1
2
3
4
√
已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为( )
A.梯形 B.菱形 C.矩形 D.正方形
解析
1
2
3
4
√
解析
1
2
3
4
√
在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为AC的中点,则cos∠BDC等于
如图,建立平面直角坐标系,
则B(0,0),A(0,8),C(6,0),D(3,4),
1
2
3
4
1
解析
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
