6.4.2 向量在物理中的应用举例-高中数学人教A版(2019)必修二 课件(共18张PPT)
文档属性
| 名称 | 6.4.2 向量在物理中的应用举例-高中数学人教A版(2019)必修二 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 778.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
向量在物理中的应用举例
学习目标
会用向量方法解决简单的力学问题及其他实际问题,
体会向量在解决物理和实际问题中的作用.
高一(8)班和高一(5)的同学在草地进行拔河比赛,身为高一(8)班体育委员的你,将会如果指导同学们的具体比赛,让大家的劲使往一处呢?
该朝什么方向使劲啊?
向量与力
1
例1
解
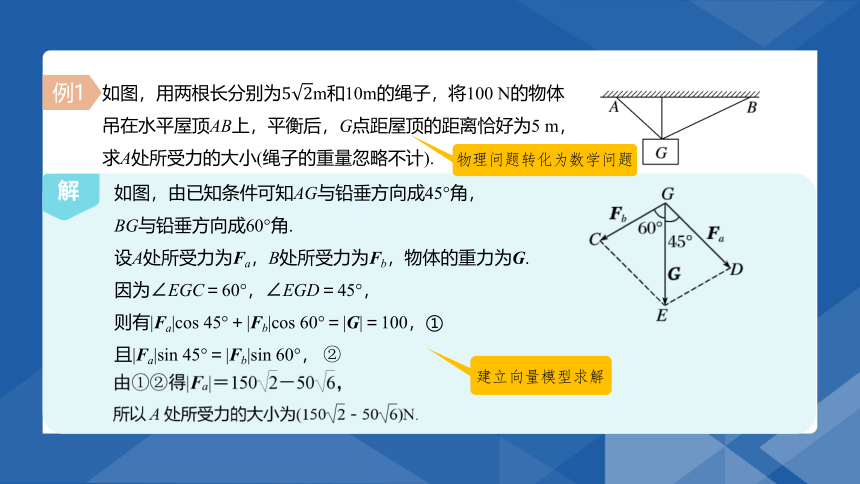
如图,用两根长分别为m和10m的绳子,将100 N的物体
吊在水平屋顶AB上,平衡后,G点距屋顶的距离恰好为5 m,
求A处所受力的大小(绳子的重量忽略不计).
物理问题转化为数学问题
如图,由已知条件可知AG与铅垂方向成45°角,
BG与铅垂方向成60°角.
设A处所受力为Fa,B处所受力为Fb,物体的重力为G.
因为∠EGC=60°,∠EGD=45°,
则有|Fa|cos 45°+|Fb|cos 60°=|G|=100,①
且|Fa|sin 45°=|Fb|sin 60°, ②
建立向量模型求解
反思感悟
利用向量解决物理问题的一般步骤
①
问题的转化,即把物理问题转化为数学问题
②
模型的建立,即建立以向量为主体的数学模型
③
参数的获得,即求出数学模型的有关解——理论参数值
④
参数的获得,即求出数学模型的有关解——理论参数值
跟踪训练1
解 由题意|F3|=|F1+F2|,
跟踪训练1
解 设F2与F3的夹角为θ,因为F3=-(F1+F2),
所以F3·F2=-F1·F2-F2·F2,
向量与速度、加速度、位移
2
(教材P41例4改编)一条宽为km的河,水流速度为2km/h,在河两岸有两个码头A、B,已知AB= km,船在水中的最大航速为4 km/h,问该船怎样安排航行速度可使它从A码头最快到达彼岸B码头?用时多少?
例2
解
以AC和AD为邻边作□ ACED,且当AE与AB重合时能最快到达彼岸,
根据题意知AC⊥AE,在Rt△ADE和□ACED中,
∴该船实际航行速度大小为4 km/h,与水流方向成120°角时能最快到达B码头,用时0.5 h.
确定最快条件
结合图形求解角度
反思感悟
速度、加速度、位移的合成与分解
实质
向量的加、减运算
途径
向量的线性运算
向量的坐标运算
跟踪训练2
一艘船以4 km/h的速度沿着与水流方向成120°的方向航行,已知水流速度为2 km/h,若船的实际航行方向与水流方向垂直,则经过3 h,该船的实际航程为_____km.
向量与功
3
例3
解
已知力F(斜向上)与水平方向的夹角为30°,大小为50 N,一个质量为8 kg的木块受力F的作用在动摩擦因数μ=0.02的水平面上运动了20 m.问力F和摩擦力f所做的功分别为多少?(g=10 m/s2)
如图所示,设木块的位移为s,
将力F分解,它在铅垂方向上的分力F1的大小为
所以摩擦力f 的大小为| f |=|μ(G-F1)|=(80-25)×0.02=1.1(N),
因此Wf=f·s=| f ||s|cos 180°=1.1×20×(-1)=-22(J).
W=F·s=|F||s|cos θ(θ为F和s的夹角)
反思感悟
力所做的功
定义
力在物体前进方向上的分力与物体位移的乘积
实质
力和位移两个向量的数量积,即W=F·s=|F||s|cos θ(θ为F和s的夹角)
跟踪训练3
在平面直角坐标系中,力F=(2,3)作用于一物体,使物体从点A(2,0)移动到点B(4,0),则力F对物体作的功为_____.
4
又F=(2,3),
课堂小结
1. 知识清单:
(1)利用向量的加、减、数乘运算解决力、位移、速度、加速度的合成与分解
(2)利用向量的数量积解决力所做的功的问题
2. 方法归纳:
转化法
3. 常见误区:
不能将物理问题转化为向量问题
向量在物理中的应用举例
学习目标
会用向量方法解决简单的力学问题及其他实际问题,
体会向量在解决物理和实际问题中的作用.
高一(8)班和高一(5)的同学在草地进行拔河比赛,身为高一(8)班体育委员的你,将会如果指导同学们的具体比赛,让大家的劲使往一处呢?
该朝什么方向使劲啊?
向量与力
1
例1
解
如图,用两根长分别为m和10m的绳子,将100 N的物体
吊在水平屋顶AB上,平衡后,G点距屋顶的距离恰好为5 m,
求A处所受力的大小(绳子的重量忽略不计).
物理问题转化为数学问题
如图,由已知条件可知AG与铅垂方向成45°角,
BG与铅垂方向成60°角.
设A处所受力为Fa,B处所受力为Fb,物体的重力为G.
因为∠EGC=60°,∠EGD=45°,
则有|Fa|cos 45°+|Fb|cos 60°=|G|=100,①
且|Fa|sin 45°=|Fb|sin 60°, ②
建立向量模型求解
反思感悟
利用向量解决物理问题的一般步骤
①
问题的转化,即把物理问题转化为数学问题
②
模型的建立,即建立以向量为主体的数学模型
③
参数的获得,即求出数学模型的有关解——理论参数值
④
参数的获得,即求出数学模型的有关解——理论参数值
跟踪训练1
解 由题意|F3|=|F1+F2|,
跟踪训练1
解 设F2与F3的夹角为θ,因为F3=-(F1+F2),
所以F3·F2=-F1·F2-F2·F2,
向量与速度、加速度、位移
2
(教材P41例4改编)一条宽为km的河,水流速度为2km/h,在河两岸有两个码头A、B,已知AB= km,船在水中的最大航速为4 km/h,问该船怎样安排航行速度可使它从A码头最快到达彼岸B码头?用时多少?
例2
解
以AC和AD为邻边作□ ACED,且当AE与AB重合时能最快到达彼岸,
根据题意知AC⊥AE,在Rt△ADE和□ACED中,
∴该船实际航行速度大小为4 km/h,与水流方向成120°角时能最快到达B码头,用时0.5 h.
确定最快条件
结合图形求解角度
反思感悟
速度、加速度、位移的合成与分解
实质
向量的加、减运算
途径
向量的线性运算
向量的坐标运算
跟踪训练2
一艘船以4 km/h的速度沿着与水流方向成120°的方向航行,已知水流速度为2 km/h,若船的实际航行方向与水流方向垂直,则经过3 h,该船的实际航程为_____km.
向量与功
3
例3
解
已知力F(斜向上)与水平方向的夹角为30°,大小为50 N,一个质量为8 kg的木块受力F的作用在动摩擦因数μ=0.02的水平面上运动了20 m.问力F和摩擦力f所做的功分别为多少?(g=10 m/s2)
如图所示,设木块的位移为s,
将力F分解,它在铅垂方向上的分力F1的大小为
所以摩擦力f 的大小为| f |=|μ(G-F1)|=(80-25)×0.02=1.1(N),
因此Wf=f·s=| f ||s|cos 180°=1.1×20×(-1)=-22(J).
W=F·s=|F||s|cos θ(θ为F和s的夹角)
反思感悟
力所做的功
定义
力在物体前进方向上的分力与物体位移的乘积
实质
力和位移两个向量的数量积,即W=F·s=|F||s|cos θ(θ为F和s的夹角)
跟踪训练3
在平面直角坐标系中,力F=(2,3)作用于一物体,使物体从点A(2,0)移动到点B(4,0),则力F对物体作的功为_____.
4
又F=(2,3),
课堂小结
1. 知识清单:
(1)利用向量的加、减、数乘运算解决力、位移、速度、加速度的合成与分解
(2)利用向量的数量积解决力所做的功的问题
2. 方法归纳:
转化法
3. 常见误区:
不能将物理问题转化为向量问题
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
