8.1.2圆柱、圆锥、圆台、球、简单组合体-高中数学人教A版(2019)必修二课件(共29张PPT)
文档属性
| 名称 | 8.1.2圆柱、圆锥、圆台、球、简单组合体-高中数学人教A版(2019)必修二课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 19:21:28 | ||
图片预览







文档简介
(共29张PPT)
圆柱、圆锥、圆台、球、简单组合体
第八章 立体几何初步
学习目标
1.了解圆柱、圆锥、圆台、球的定义.
2.掌握圆柱、圆锥、圆台、球的结构特征.
3.了解简单组合体的概念及结构特征.
你到过孔子六艺城吗?在孔子六艺城中有一个地方是数学爱好者必去的,那就是“数厅”,如图,以圆柱体为底托,巨型球体悬其之上,形成了国内少有的圆形建筑物,甚为壮观,你知道其中隐含的数学知识吗?
1
旋转体的结构特征
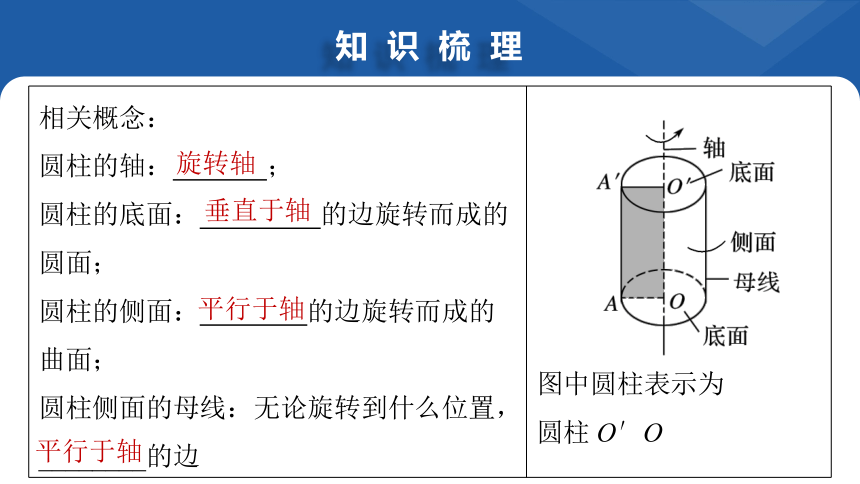
1.圆柱的概念及结构特征
圆柱 图形及表示
定义:以 所在直线为旋转轴,其余三边旋转 形成的 所围成的旋转体叫做圆柱
矩形的一边
一周
面
阅读课本第101-103页,完成以下内容.
相关概念: 圆柱的轴: ; 圆柱的底面: 的边旋转而成的圆面; 圆柱的侧面: 的边旋转而成的曲面; 圆柱侧面的母线:无论旋转到什么位置, ________的边
图中圆柱表示为
圆柱 O′O
旋转轴
垂直于轴
平行于轴
平行于轴
圆锥 图形及表示
定义:以直角三角形的___________ 所在直线为旋转轴,其余两边旋转 _____形成的面所围成的旋转体
一条直角边
一周
2.圆锥的概念及结构特征
相关概念:圆锥的轴:旋转轴; 圆锥的底面: 轴的边旋转而成的圆面; 侧面:直角三角形的 旋转而成的曲面; 母线:无论旋转到什么位置 , 轴的边
图中圆锥表示为圆锥SO
垂直于
不垂直于
斜边
圆台 图形及表示
定义:用 的平面去截圆锥, 之间的部分叫做圆台
3.圆台的概念及结构特征
平行于圆锥底面
底面与截面
相关概念: 圆台的轴:旋转轴; 圆台的底面: 轴的边旋转一周所形成的圆面; 圆台的侧面: 轴的边旋转一周所形成的曲面; 母线:无论旋转到什么位置,_________ 轴的边
图中圆台表示为圆台O′O
垂直于
不垂直于
不垂直于
球 图形及表示
定义: 所在直线为旋转轴,旋转 形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称___
4.球的概念及结构特征
半圆以它的直径
一周
球
相关概念: 球心:半圆的 ; 半径:连接 和球面上任意一点的 ; 直径:连接球面上 并且经过球心的___________
图中的球表示为球O
圆心
球心
两点
线段
线段
5.棱柱与圆柱统称为 ,棱锥与圆锥统称为 ,棱台与 统称为台体.
柱体
锥体
圆台
柱体
锥体
台体
例1 (多选)下列选项中,正确的是
A.以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台
B.圆柱、圆锥、圆台的底面都是圆
C.以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋
转一周形成的曲面所围成的几何体是圆锥
D.用一个平面去截球,得到的截面是一个圆面
解析 A中,以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
B中,它们的底面为圆面;C,D正确.
√
√
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成.
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练1 (多选)下列说法,正确的是
A.圆柱的母线与它的轴可以不平行
B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的
连线都可以构成直角三角形
C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线
D.圆柱的任意两条母线所在直线是互相平行的
√
√
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
2
简单组合体的结构特征
现实世界中的物体表示的几何体,除柱体、锥体、台体和球等简单的几何体外,还有大量的几何体是由简单几何体组合而成的,这些几何体称作 ,简单组合体的构成有两种基本形式:一种是由简单几何体 而成,一种是由简单几何体
一部分而成.
简单组合体
拼接
截去或挖去
阅读课本第103页,完成以下内容.
解 图(1)是由两个圆台拼接而成的组合体;
图(2)是由圆台挖去一个圆锥后得到的几何体;
图(3)是由一个圆柱挖去一个三棱柱后得到的几何体.
例2 (1)请描述如图所示的几何体是如何形成的.
解析 此几何体自上向下由一个圆锥、两个圆台和一个圆柱构成,是由A中的平面图形旋转而形成的.
(2) 如图所示的几何体是由下面哪一个平面图形旋转而形成的
√
延伸探究 将本例中的组合体变为下面左侧图,则由下列所示的哪个三角形绕直线l旋转一周可以得到
解析 A的旋转体是圆锥,不满足题意;
B的旋转体是两个圆锥,满足题意;
C的旋转体是圆锥不满足题意;
D的旋转体是圆柱挖去一个圆锥的几何体,不满足题意.
√
跟踪训练2
(1)如图所示的简单组合体的组成是
A.棱柱、棱台 B.棱柱、棱锥
C.棱锥、棱台 D.棱柱、棱柱
√
解析 图①是一个等腰梯形,CD为较长的
底边,以CD边所在直线为旋转轴旋转一周
所得几何体为一个组合体,
如图②,包括一个圆柱、两个圆锥.
(2) 将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
√
3
旋转体的有关计算
例3 如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台O′O的母线长.
解 设圆台的母线长为l cm,由截得的圆台上、下底面面积之比为1∶16,可设截得的圆台的上、下底面的半径分别为r cm,4r cm.过轴SO作截面,如图所示.
则△SO′A′∽△SOA,SA′=3 cm.
解得l=9,即圆台的母线长为9 cm.
(1)用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形中的相似比,构设相关几何变量的方程(组)而得解.
(2)利用球的截面,将立体问题转化为平面问题是解决球的有关问题的关键.
跟踪训练3 某地球仪上北纬30°纬线圈的长度为12π cm,如图所示,则该地球仪的半径是________cm.
解析 如图所示,
由题意知,北纬30°所在小圆的周长为12π,
则该小圆的半径r=6,其中∠ABO=30°,
课堂小结
1.知识清单:
(1)圆柱、圆锥、圆台的结构特征.
(2)球的结构特征.
(3)简单组合体的结构特征.
2.方法归纳:分类讨论、转化与化归.
3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不同的.
圆柱、圆锥、圆台、球、简单组合体
第八章 立体几何初步
学习目标
1.了解圆柱、圆锥、圆台、球的定义.
2.掌握圆柱、圆锥、圆台、球的结构特征.
3.了解简单组合体的概念及结构特征.
你到过孔子六艺城吗?在孔子六艺城中有一个地方是数学爱好者必去的,那就是“数厅”,如图,以圆柱体为底托,巨型球体悬其之上,形成了国内少有的圆形建筑物,甚为壮观,你知道其中隐含的数学知识吗?
1
旋转体的结构特征
1.圆柱的概念及结构特征
圆柱 图形及表示
定义:以 所在直线为旋转轴,其余三边旋转 形成的 所围成的旋转体叫做圆柱
矩形的一边
一周
面
阅读课本第101-103页,完成以下内容.
相关概念: 圆柱的轴: ; 圆柱的底面: 的边旋转而成的圆面; 圆柱的侧面: 的边旋转而成的曲面; 圆柱侧面的母线:无论旋转到什么位置, ________的边
图中圆柱表示为
圆柱 O′O
旋转轴
垂直于轴
平行于轴
平行于轴
圆锥 图形及表示
定义:以直角三角形的___________ 所在直线为旋转轴,其余两边旋转 _____形成的面所围成的旋转体
一条直角边
一周
2.圆锥的概念及结构特征
相关概念:圆锥的轴:旋转轴; 圆锥的底面: 轴的边旋转而成的圆面; 侧面:直角三角形的 旋转而成的曲面; 母线:无论旋转到什么位置 , 轴的边
图中圆锥表示为圆锥SO
垂直于
不垂直于
斜边
圆台 图形及表示
定义:用 的平面去截圆锥, 之间的部分叫做圆台
3.圆台的概念及结构特征
平行于圆锥底面
底面与截面
相关概念: 圆台的轴:旋转轴; 圆台的底面: 轴的边旋转一周所形成的圆面; 圆台的侧面: 轴的边旋转一周所形成的曲面; 母线:无论旋转到什么位置,_________ 轴的边
图中圆台表示为圆台O′O
垂直于
不垂直于
不垂直于
球 图形及表示
定义: 所在直线为旋转轴,旋转 形成的曲面叫做球面,球面所围成的旋转体叫做球体,简称___
4.球的概念及结构特征
半圆以它的直径
一周
球
相关概念: 球心:半圆的 ; 半径:连接 和球面上任意一点的 ; 直径:连接球面上 并且经过球心的___________
图中的球表示为球O
圆心
球心
两点
线段
线段
5.棱柱与圆柱统称为 ,棱锥与圆锥统称为 ,棱台与 统称为台体.
柱体
锥体
圆台
柱体
锥体
台体
例1 (多选)下列选项中,正确的是
A.以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台
B.圆柱、圆锥、圆台的底面都是圆
C.以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋
转一周形成的曲面所围成的几何体是圆锥
D.用一个平面去截球,得到的截面是一个圆面
解析 A中,以直角梯形垂直于底边的一腰所在直线为轴旋转一周可得到圆台;
B中,它们的底面为圆面;C,D正确.
√
√
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成.
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
跟踪训练1 (多选)下列说法,正确的是
A.圆柱的母线与它的轴可以不平行
B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的
连线都可以构成直角三角形
C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线
D.圆柱的任意两条母线所在直线是互相平行的
√
√
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
2
简单组合体的结构特征
现实世界中的物体表示的几何体,除柱体、锥体、台体和球等简单的几何体外,还有大量的几何体是由简单几何体组合而成的,这些几何体称作 ,简单组合体的构成有两种基本形式:一种是由简单几何体 而成,一种是由简单几何体
一部分而成.
简单组合体
拼接
截去或挖去
阅读课本第103页,完成以下内容.
解 图(1)是由两个圆台拼接而成的组合体;
图(2)是由圆台挖去一个圆锥后得到的几何体;
图(3)是由一个圆柱挖去一个三棱柱后得到的几何体.
例2 (1)请描述如图所示的几何体是如何形成的.
解析 此几何体自上向下由一个圆锥、两个圆台和一个圆柱构成,是由A中的平面图形旋转而形成的.
(2) 如图所示的几何体是由下面哪一个平面图形旋转而形成的
√
延伸探究 将本例中的组合体变为下面左侧图,则由下列所示的哪个三角形绕直线l旋转一周可以得到
解析 A的旋转体是圆锥,不满足题意;
B的旋转体是两个圆锥,满足题意;
C的旋转体是圆锥不满足题意;
D的旋转体是圆柱挖去一个圆锥的几何体,不满足题意.
√
跟踪训练2
(1)如图所示的简单组合体的组成是
A.棱柱、棱台 B.棱柱、棱锥
C.棱锥、棱台 D.棱柱、棱柱
√
解析 图①是一个等腰梯形,CD为较长的
底边,以CD边所在直线为旋转轴旋转一周
所得几何体为一个组合体,
如图②,包括一个圆柱、两个圆锥.
(2) 将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
√
3
旋转体的有关计算
例3 如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台O′O的母线长.
解 设圆台的母线长为l cm,由截得的圆台上、下底面面积之比为1∶16,可设截得的圆台的上、下底面的半径分别为r cm,4r cm.过轴SO作截面,如图所示.
则△SO′A′∽△SOA,SA′=3 cm.
解得l=9,即圆台的母线长为9 cm.
(1)用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形中的相似比,构设相关几何变量的方程(组)而得解.
(2)利用球的截面,将立体问题转化为平面问题是解决球的有关问题的关键.
跟踪训练3 某地球仪上北纬30°纬线圈的长度为12π cm,如图所示,则该地球仪的半径是________cm.
解析 如图所示,
由题意知,北纬30°所在小圆的周长为12π,
则该小圆的半径r=6,其中∠ABO=30°,
课堂小结
1.知识清单:
(1)圆柱、圆锥、圆台的结构特征.
(2)球的结构特征.
(3)简单组合体的结构特征.
2.方法归纳:分类讨论、转化与化归.
3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不同的.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
