8.5.3 平面与平面平行-高中数学人教A版(2019)必修二课件(共30张PPT)
文档属性
| 名称 | 8.5.3 平面与平面平行-高中数学人教A版(2019)必修二课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 19:28:00 | ||
图片预览










文档简介
(共30张PPT)
平面与平面平行
第八章 立体几何初步
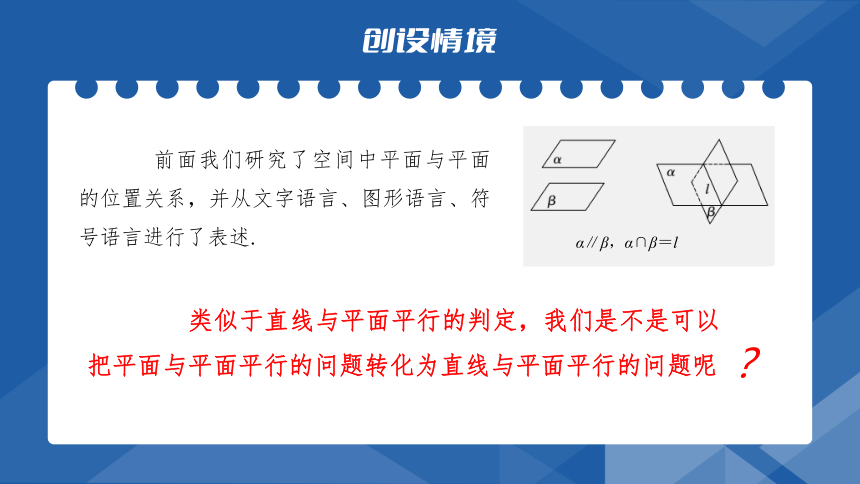
前面我们研究了空间中平面与平面的位置关系,并从文字语言、图形语言、符号语言进行了表述.
类似于直线与平面平行的判定,我们是不是可以把平面与平面平行的问题转化为直线与平面平行的问题呢
?
α∥β,α∩β=l
平面与平面平行的判定定理
1
阅读课本第139-140页,完成以下内容.
问题1
三角尺和桌面一定平行,硬纸片不一定平行.
提示
如图(1),a和b分别是矩形硬纸片的两条对边所在直线,它们都和桌面平行,那么硬纸片和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺和桌面平行吗?
即如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
文字语言
知识梳理
图形语言
a β, ,
,
,b∥α
如果一个平面内的 与另一个平面平行,那么这两个平面平行
两条相交直线
符号语言
平面与平面平行的判定定理
a∩b=P
b β
a∥α
β∥α
例1
解析 对A,当α∩β=a,l∥m∥a时,不能推出α∥β;
对B,当α∩β=a,且在平面α内同侧有两点,另一侧有一个点,三点到平面β的距离相等时,不能推出α∥β;
对C,当l∥m时,不能推出α∥β;
对D,∵l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,∴α内存在两条相交直线与平面β平行,故可得α∥β.
(1)α,β是两个不重合的平面,在下列条件下,可判定α∥β的是
A.α,β都平行于直线l,m
B.α内有三个不共线的点到β的距离相等
C.l,m是α内的两条直线且l∥β,m∥β
D.l,m是异面直线且l∥α,m∥α,l∥β,m∥β
√
例1
∵ABCD-A1B1C1D1为正方体
证明
(2)已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面BC1D.
∴D1C1∥A1B1,AB∥ A1B1 ,
∴D1C1∥AB,
∴四边形D1C1BA为平行四边形. ∴D1A∥C1B.
又D1A 平面BC1D,C1B 平面BC1D,∴D1A∥平面BC1D.
同理D1B1∥平面BC1D.
又D1A∩D1B1=D1,D1A,D1B1 平面AB1D1,
∴平面AB1D1∥平面BC1D.
例1
连接B1D1,NE,如图所示.
∵在△B1C1D1中,E,F分别为C1D1,B1C1的中点,∴EF∥B1D1,
同理MN∥B1D1,∴MN∥EF,
又∵EF 平面BDEF,MN 平面BDEF,∴MN∥平面BDEF.
在正方形A1B1C1D1中ABCD ,N,E分别为A1B1,C1D1的中点,
∴ NE ∥ A1D1 ,又 ∵ A1D1∥AD∴ NE ∥AD.
证明
延伸探究 在正方体ABCD-A1B1C1D1中,M,N,E,F分别是A1D1,A1B1,C1D1,B1C1的中点,求证:平面AMN∥平面BDEF.
∴四边形ADEN是平行四边形,
∴AN∥DE,
又∵AN 平面BDEF,DE 平面BDEF,
∴AN∥平面BDEF,
又∵AN∩MN=N且AN,MN 平面AMN,
∴平面AMN∥平面BDEF.
反思感悟
③转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β.
平面与平面平行的判定方法
①定义法:两个平面没有公共点.
②判定定理:一个平面内的两条相交直线分别平行于另一个平面.
④利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.
反思感悟
在判定两个平面是否平行时,一定要强调一个平面内的“两条相交直线”这个条件
判定两个平面是否平行的注意事项
线不在多
相交就行
跟踪训练1
(1)如果一个锐角的两边与另一个角的两边分别平行,下列结论一定成立的是
A.这两个角相等
B.这两个角互补
C.这两个角所在的两个平面平行
D.这两个角所在的两个平面平行或重合
√
跟踪训练1
(2)如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
跟踪训练1
证明 ∵E,G分别是PC,BC的中点,
∴EG∥PB,
又∵EG 平面PAB,PB 平面PAB,
∴EG∥平面PAB,
∵E,F分别是PC,PD的中点,
∴EF∥CD,又∵AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
平面与平面平行的性质
2
阅读课本第141-142页,完成以下内容.
问题3
直线a与平面β平行.直线a与平面β内的直线b平行或异面.
当a与b不异面,即在同一个平面内时平行.即两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行.
提示
若两平面α与β平行,那么平面α内的直线a与平面β有何位置关系?平面α内的直线a与平面β内的任一直线b有何位置关系?何时a与b平行?
阅读课本第141-142页,完成以下内容.
问题3
提示 如图,平面α∥β,平面γ分别与平面α,β相交于直线a,b.
∵α∩γ=a,β∩γ=b,
∴a α,b β.
又α∥β,
∴a,b没有公共点.
又a,b同在平面γ内,∴a∥b.
你能证明你得到的结论吗?
文字语言
知识梳理
图形语言
α∥β,α∩γ=a,β∩γ=b _____.
两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______.
平行
符号语言
两个平面平行的性质定理
a∥b
如图,在正方体ABCD-A1B1C1D1中,E为棱AA1的中点,过点B,E,D1的平面与棱CC1交于点F.
(1)求证:四边形BFD1E为平行四边形;
例2
证明 在正方体ABCD-A1B1C1D1中,
平面ABB1A1∥平面DCC1D1,
且平面BFD1E∩平面ABB1A1=BE,平面BFD1E∩平面DCC1D1=FD1,
由面面平行的性质定理知BE∥FD1,
同理BF∥D1E,∴四边形BFD1E为平行四边形.
例2
(2)试确定点F的位置.
解 取BB1的中点M,连接MC1,ME,如图,
∵M,E分别为棱BB1,AA1的中点,∴ ME ∥A1B1,
又A1B1∥C1D1∴ ME ∥C1D1∴四边形D1EMC1为平行四边形,
∴D1E∥MC1,又D1E∥BF,∴MC1∥BF,又C1F∥BM,
∴四边形MBFC1为平行四边形,∴BM∥C1F
∴F为棱CC1的中点.
反思感悟
③再找一个平面,使这两条直线都在这个平面上.
利用面面平行的性质定理判断两直线平行的步骤
①先找两个平面,使这两个平面分别经过这两条直线中的一条.
②判定这两个平面平行(此条件有时题目会直接给出).
④由定理得出结论.
跟踪训练2
如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF,
求证:NF∥CM.
证明 因为D,E分别是PA,PB的中点,所以DE∥AB.
又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC,
同理DF∥平面ABC,且DE∩DF=D,DE,DF 平面DEF,
所以平面DEF∥平面ABC.
又平面PCM∩平面DEF=NF,平面PCM∩平面ABC=CM,
所以NF∥CM.
平行关系的综合应用
3
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;
例3
证明 如图,连接AC,CD1.因为四边形ABCD是正方形,
且Q是BD的中点,所以Q是AC的中点,
又P是AD1的中点,所以PQ∥CD1.
又PQ 平面DCC1D1,CD1 平面DCC1D1,
所以PQ∥平面DCC1D1.
例3
(2)求PQ的长;
例3
(3)求证:EF∥平面BB1D1D.
证明 方法一 取B1D1的中点O1,连接FO1,BO1,如图所示,
所以BE∥FO1,BE=FO1,
所以四边形BEFO1为平行四边形,
所以EF∥BO1.
又EF 平面BB1D1D,BO1 平面BB1D1D,
所以EF∥平面BB1D1D.
例3
(3)求证:EF∥平面BB1D1D.
方法二 取B1C1的中点E1,连接EE1,FE1,如图所示,
则有FE1∥B1D1,EE1∥BB1,
且FE1∩EE1=E1,B1D1∩BB1=B1,
FE1,EE1 平面EE1F,B1D1,BB1 平面BB1D1D,
所以平面EE1F∥平面BB1D1D.
又EF 平面EE1F,
所以EF∥平面BB1D1D.
反思感悟
线线平行、线面平行、面面平行是一个有机的整体,平行关系的判定定理、性质定理是转化平行关系的关键.
平行关系的判定定理、性质定理的内在联系
内在联系
跟踪训练3
如图,已知平面α∥平面β,P α且P β,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D,且PA=6,AC=9,PD=8,求BD的长.
解 ∵α∥β,平面PCD∩α=AB,平面PCD∩β=CD,
∵PA=6,AC=9,PD=8,
课堂小结
1. 知识清单:
(1)平面与平面平行的判定定理.
(2)平面与平面平行的性质定理.
(3)平行关系的综合应用.
2. 方法归纳:转化与化归.
3. 常见误区:平面与平面平行的条件不充分.
平面与平面平行
第八章 立体几何初步
前面我们研究了空间中平面与平面的位置关系,并从文字语言、图形语言、符号语言进行了表述.
类似于直线与平面平行的判定,我们是不是可以把平面与平面平行的问题转化为直线与平面平行的问题呢
?
α∥β,α∩β=l
平面与平面平行的判定定理
1
阅读课本第139-140页,完成以下内容.
问题1
三角尺和桌面一定平行,硬纸片不一定平行.
提示
如图(1),a和b分别是矩形硬纸片的两条对边所在直线,它们都和桌面平行,那么硬纸片和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺和桌面平行吗?
即如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
文字语言
知识梳理
图形语言
a β, ,
,
,b∥α
如果一个平面内的 与另一个平面平行,那么这两个平面平行
两条相交直线
符号语言
平面与平面平行的判定定理
a∩b=P
b β
a∥α
β∥α
例1
解析 对A,当α∩β=a,l∥m∥a时,不能推出α∥β;
对B,当α∩β=a,且在平面α内同侧有两点,另一侧有一个点,三点到平面β的距离相等时,不能推出α∥β;
对C,当l∥m时,不能推出α∥β;
对D,∵l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,∴α内存在两条相交直线与平面β平行,故可得α∥β.
(1)α,β是两个不重合的平面,在下列条件下,可判定α∥β的是
A.α,β都平行于直线l,m
B.α内有三个不共线的点到β的距离相等
C.l,m是α内的两条直线且l∥β,m∥β
D.l,m是异面直线且l∥α,m∥α,l∥β,m∥β
√
例1
∵ABCD-A1B1C1D1为正方体
证明
(2)已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面BC1D.
∴D1C1∥A1B1,AB∥ A1B1 ,
∴D1C1∥AB,
∴四边形D1C1BA为平行四边形. ∴D1A∥C1B.
又D1A 平面BC1D,C1B 平面BC1D,∴D1A∥平面BC1D.
同理D1B1∥平面BC1D.
又D1A∩D1B1=D1,D1A,D1B1 平面AB1D1,
∴平面AB1D1∥平面BC1D.
例1
连接B1D1,NE,如图所示.
∵在△B1C1D1中,E,F分别为C1D1,B1C1的中点,∴EF∥B1D1,
同理MN∥B1D1,∴MN∥EF,
又∵EF 平面BDEF,MN 平面BDEF,∴MN∥平面BDEF.
在正方形A1B1C1D1中ABCD ,N,E分别为A1B1,C1D1的中点,
∴ NE ∥ A1D1 ,又 ∵ A1D1∥AD∴ NE ∥AD.
证明
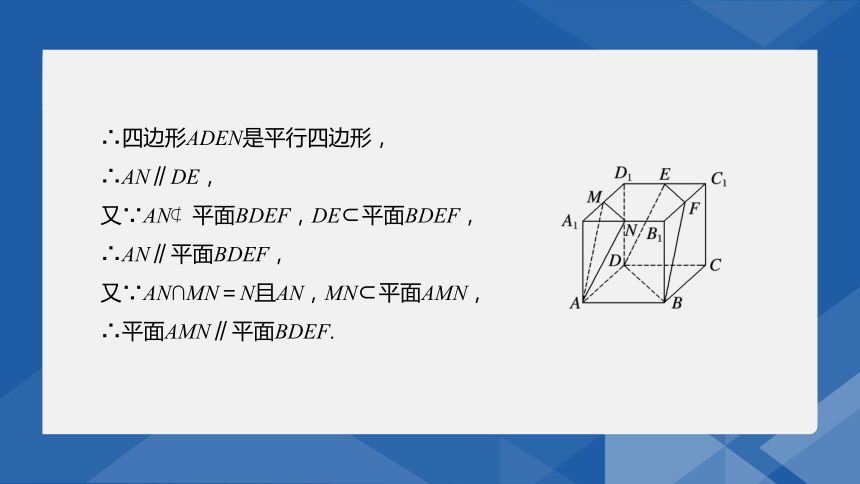
延伸探究 在正方体ABCD-A1B1C1D1中,M,N,E,F分别是A1D1,A1B1,C1D1,B1C1的中点,求证:平面AMN∥平面BDEF.
∴四边形ADEN是平行四边形,
∴AN∥DE,
又∵AN 平面BDEF,DE 平面BDEF,
∴AN∥平面BDEF,
又∵AN∩MN=N且AN,MN 平面AMN,
∴平面AMN∥平面BDEF.
反思感悟
③转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β.
平面与平面平行的判定方法
①定义法:两个平面没有公共点.
②判定定理:一个平面内的两条相交直线分别平行于另一个平面.
④利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.
反思感悟
在判定两个平面是否平行时,一定要强调一个平面内的“两条相交直线”这个条件
判定两个平面是否平行的注意事项
线不在多
相交就行
跟踪训练1
(1)如果一个锐角的两边与另一个角的两边分别平行,下列结论一定成立的是
A.这两个角相等
B.这两个角互补
C.这两个角所在的两个平面平行
D.这两个角所在的两个平面平行或重合
√
跟踪训练1
(2)如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
跟踪训练1
证明 ∵E,G分别是PC,BC的中点,
∴EG∥PB,
又∵EG 平面PAB,PB 平面PAB,
∴EG∥平面PAB,
∵E,F分别是PC,PD的中点,
∴EF∥CD,又∵AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
平面与平面平行的性质
2
阅读课本第141-142页,完成以下内容.
问题3
直线a与平面β平行.直线a与平面β内的直线b平行或异面.
当a与b不异面,即在同一个平面内时平行.即两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行.
提示
若两平面α与β平行,那么平面α内的直线a与平面β有何位置关系?平面α内的直线a与平面β内的任一直线b有何位置关系?何时a与b平行?
阅读课本第141-142页,完成以下内容.
问题3
提示 如图,平面α∥β,平面γ分别与平面α,β相交于直线a,b.
∵α∩γ=a,β∩γ=b,
∴a α,b β.
又α∥β,
∴a,b没有公共点.
又a,b同在平面γ内,∴a∥b.
你能证明你得到的结论吗?
文字语言
知识梳理
图形语言
α∥β,α∩γ=a,β∩γ=b _____.
两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______.
平行
符号语言
两个平面平行的性质定理
a∥b
如图,在正方体ABCD-A1B1C1D1中,E为棱AA1的中点,过点B,E,D1的平面与棱CC1交于点F.
(1)求证:四边形BFD1E为平行四边形;
例2
证明 在正方体ABCD-A1B1C1D1中,
平面ABB1A1∥平面DCC1D1,
且平面BFD1E∩平面ABB1A1=BE,平面BFD1E∩平面DCC1D1=FD1,
由面面平行的性质定理知BE∥FD1,
同理BF∥D1E,∴四边形BFD1E为平行四边形.
例2
(2)试确定点F的位置.
解 取BB1的中点M,连接MC1,ME,如图,
∵M,E分别为棱BB1,AA1的中点,∴ ME ∥A1B1,
又A1B1∥C1D1∴ ME ∥C1D1∴四边形D1EMC1为平行四边形,
∴D1E∥MC1,又D1E∥BF,∴MC1∥BF,又C1F∥BM,
∴四边形MBFC1为平行四边形,∴BM∥C1F
∴F为棱CC1的中点.
反思感悟
③再找一个平面,使这两条直线都在这个平面上.
利用面面平行的性质定理判断两直线平行的步骤
①先找两个平面,使这两个平面分别经过这两条直线中的一条.
②判定这两个平面平行(此条件有时题目会直接给出).
④由定理得出结论.
跟踪训练2
如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF,
求证:NF∥CM.
证明 因为D,E分别是PA,PB的中点,所以DE∥AB.
又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC,
同理DF∥平面ABC,且DE∩DF=D,DE,DF 平面DEF,
所以平面DEF∥平面ABC.
又平面PCM∩平面DEF=NF,平面PCM∩平面ABC=CM,
所以NF∥CM.
平行关系的综合应用
3
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;
例3
证明 如图,连接AC,CD1.因为四边形ABCD是正方形,
且Q是BD的中点,所以Q是AC的中点,
又P是AD1的中点,所以PQ∥CD1.
又PQ 平面DCC1D1,CD1 平面DCC1D1,
所以PQ∥平面DCC1D1.
例3
(2)求PQ的长;
例3
(3)求证:EF∥平面BB1D1D.
证明 方法一 取B1D1的中点O1,连接FO1,BO1,如图所示,
所以BE∥FO1,BE=FO1,
所以四边形BEFO1为平行四边形,
所以EF∥BO1.
又EF 平面BB1D1D,BO1 平面BB1D1D,
所以EF∥平面BB1D1D.
例3
(3)求证:EF∥平面BB1D1D.
方法二 取B1C1的中点E1,连接EE1,FE1,如图所示,
则有FE1∥B1D1,EE1∥BB1,
且FE1∩EE1=E1,B1D1∩BB1=B1,
FE1,EE1 平面EE1F,B1D1,BB1 平面BB1D1D,
所以平面EE1F∥平面BB1D1D.
又EF 平面EE1F,
所以EF∥平面BB1D1D.
反思感悟
线线平行、线面平行、面面平行是一个有机的整体,平行关系的判定定理、性质定理是转化平行关系的关键.
平行关系的判定定理、性质定理的内在联系
内在联系
跟踪训练3
如图,已知平面α∥平面β,P α且P β,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D,且PA=6,AC=9,PD=8,求BD的长.
解 ∵α∥β,平面PCD∩α=AB,平面PCD∩β=CD,
∵PA=6,AC=9,PD=8,
课堂小结
1. 知识清单:
(1)平面与平面平行的判定定理.
(2)平面与平面平行的性质定理.
(3)平行关系的综合应用.
2. 方法归纳:转化与化归.
3. 常见误区:平面与平面平行的条件不充分.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
