3.4 基本不等式
图片预览






文档简介
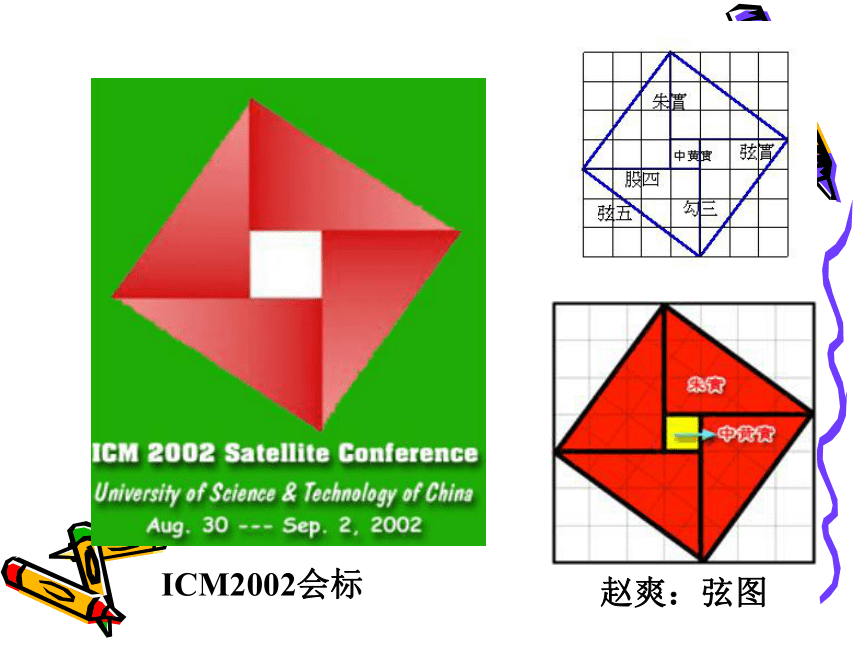
课件21张PPT。基本不等式(1)1.课题导入 如图是在北京召开的第24界国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客。
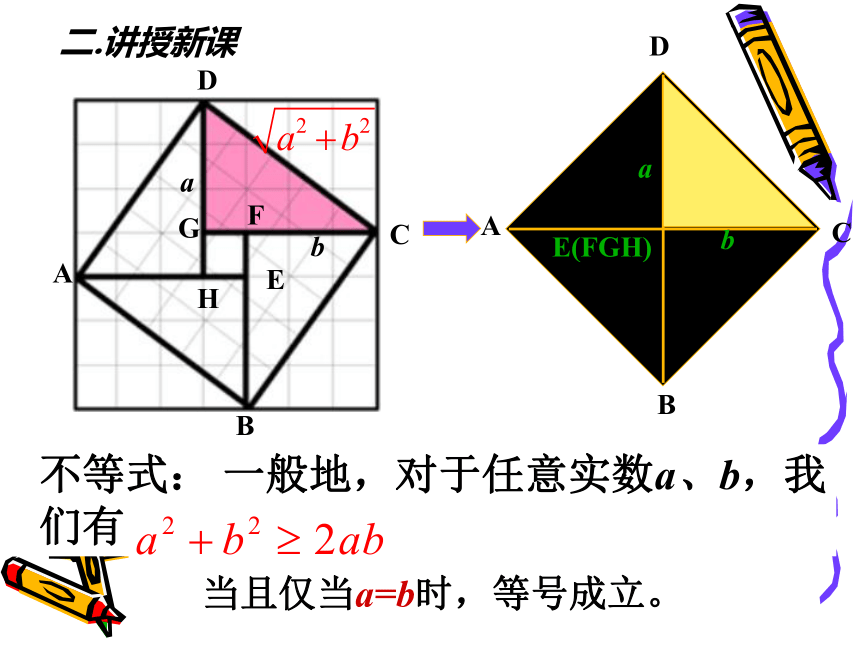
ICM2002会标赵爽:弦图你能在这个图案中找出一些相等关系或不等关系吗?二.讲授新课一般的,如果 1.重要不等式你能给出它的证明吗?如果a>0,b>0, 那么2.基本不等式此定理又可叙述为:两个正数 的算术平均数不小于它们的几何平均数. ⅱ)成立的条件是不同的:
前者只要求a,b都是实数,而后者
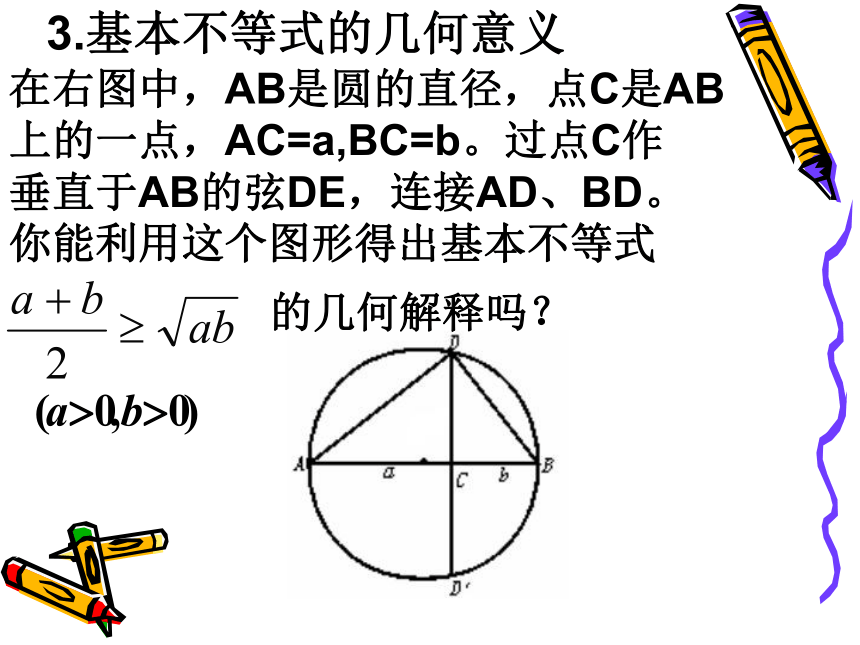
要求a,b都是正数.在右图中,AB是圆的直径,点C是AB
上的一点,AC=a,BC=b。过点C作
垂直于AB的弦DE,连接AD、BD。
你能利用这个图形得出基本不等式的几何解释吗?3.基本不等式的几何意义基本不等式的一种几何解释 基本不等式的一种几何解释 4.随堂练习 当且仅当a=12三.课堂小结1.两个不等式2.两个变形3.两种思想:数形结合的思想;转化的思想 基本不等式(2)(1)如果a, b是正数, 那么
(当且仅当 a=b 时取“=”号)基本不等式:一.复习回忆(2).两个变形应用:解决最大(小)值问题
例1、(1)用篱笆围一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这
个矩形的长、宽各为多少时,菜园的面积最大。
最大面积是多少?反思:由此题我们可以得到什么启示呢?结论:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
如果a, b是正数, 那么
(当且仅当 a=b 时取“=”号)应用:“和定积最大, 积定和最小”.剖析:利用基本不等式解决最值问题应用要点:一正 ,二定 , 三等正:两项必须都是正数; 定:求两项和的最小值,它们的积应为定值; 求两项积的最大值,它们的和应为定值。等 : 等号成立的条件必须存在.例1、?????? 例2、判断正误
(1)函数 的最小值为2
(2)函数 的最小值为2
利用均值不等式求最值应注意三点: 一正 ,二定 , 三等练习1:2.已知m 、n都是正数,且2m+n=3,
求mn的最大值 21课堂小结: 1.利用均值不等式求最值应具备三个条件,简单概括就是三个字:正、定、等
2.用基本不等式解决此类实际问题时,应按
如下步骤进行:
ICM2002会标赵爽:弦图你能在这个图案中找出一些相等关系或不等关系吗?二.讲授新课一般的,如果 1.重要不等式你能给出它的证明吗?如果a>0,b>0, 那么2.基本不等式此定理又可叙述为:两个正数 的算术平均数不小于它们的几何平均数. ⅱ)成立的条件是不同的:
前者只要求a,b都是实数,而后者
要求a,b都是正数.在右图中,AB是圆的直径,点C是AB
上的一点,AC=a,BC=b。过点C作
垂直于AB的弦DE,连接AD、BD。
你能利用这个图形得出基本不等式的几何解释吗?3.基本不等式的几何意义基本不等式的一种几何解释 基本不等式的一种几何解释 4.随堂练习 当且仅当a=12三.课堂小结1.两个不等式2.两个变形3.两种思想:数形结合的思想;转化的思想 基本不等式(2)(1)如果a, b是正数, 那么
(当且仅当 a=b 时取“=”号)基本不等式:一.复习回忆(2).两个变形应用:解决最大(小)值问题
例1、(1)用篱笆围一个面积为100m2的矩形菜园,
问这个矩形的长、宽各为多少时,所用篱笆最短。
最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这
个矩形的长、宽各为多少时,菜园的面积最大。
最大面积是多少?反思:由此题我们可以得到什么启示呢?结论:
(1)两个正数积为定值,和有最小值。
(2)两个正数和为定值,积有最大值。
如果a, b是正数, 那么
(当且仅当 a=b 时取“=”号)应用:“和定积最大, 积定和最小”.剖析:利用基本不等式解决最值问题应用要点:一正 ,二定 , 三等正:两项必须都是正数; 定:求两项和的最小值,它们的积应为定值; 求两项积的最大值,它们的和应为定值。等 : 等号成立的条件必须存在.例1、?????? 例2、判断正误
(1)函数 的最小值为2
(2)函数 的最小值为2
利用均值不等式求最值应注意三点: 一正 ,二定 , 三等练习1:2.已知m 、n都是正数,且2m+n=3,
求mn的最大值 21课堂小结: 1.利用均值不等式求最值应具备三个条件,简单概括就是三个字:正、定、等
2.用基本不等式解决此类实际问题时,应按
如下步骤进行:
