第三章 不等式小结(一)
图片预览











文档简介
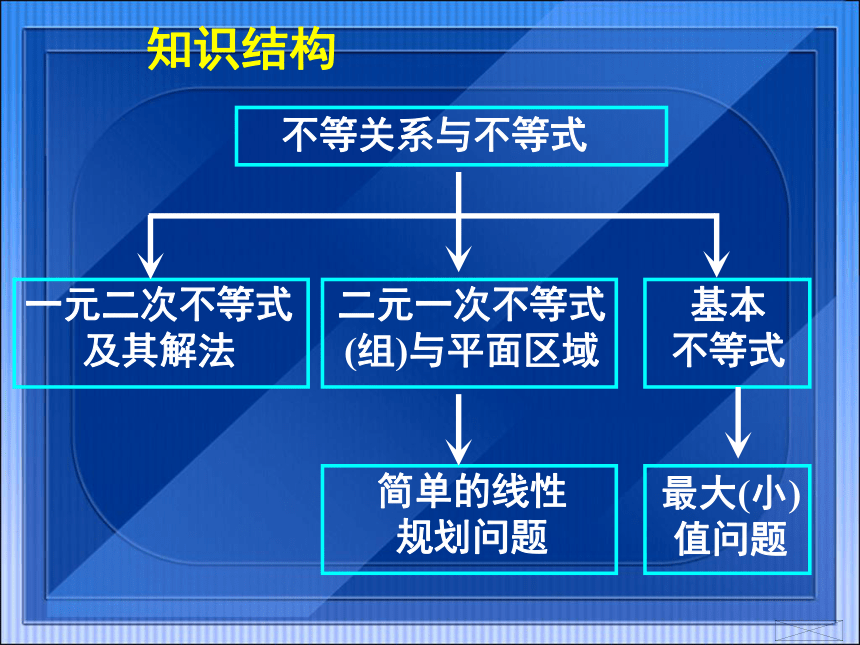
课件37张PPT。不等式小结(一)知识结构不等关系与不等式一元二次不等式
及其解法二元一次不等式
(组)与平面区域基本
不等式简单的线性
规划问题最大(小)
值问题知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理2. 应用不等式的性质比较两个实数的大小
——作差法.3. 应用不等式性质证明.知识梳理(二) 一元二次不等式及其解法一元二次不等式的解集:设相应的一元二次方程的两根为x1,x2,且x1≤x2,则不等式的解的各种情况如下表:知识梳理yxO典型例题例1. 某电脑用户计划用不超过500元的资
金购买单价分别为60元、70元的单片软件
和盒装软件,根据需要,单片软件至少买
3片,盒装软件至少买2盒,写出满足上述
不等关系的不等式.1. 用不等式表示不等关系典型例题例2. 咖啡馆配制两种饮料,甲种饮料用奶
粉、咖啡、糖,分别为9g、4g、3g;乙种
饮料用奶粉、咖啡、糖,分别为4g、5g、
5g.已知每天使用原料为奶粉3600g,咖啡
2000g,糖3000g.写出配制两种饮料杯数所
满足的所有不等关系的不等式.1. 用不等式表示不等关系典型例题2. 比较大小例3. 典型例题2. 比较大小例3. < 典型例题2. 比较大小例3. < < 典型例题2. 比较大小例3. < < < 典型例题2. 比较大小例3. 典型例题2. 比较大小例3. < 典型例题2. 比较大小例3. < < 典型例题2. 比较大小例3. < < ≥典型例题3. 利用不等式的性质求取值范围例4. 如果30<x<42,16<y<24,则
480<xy<1008.
(1) x+y的取值范围是:___________,
(2) x-2y的取值范围是:___________,
(3) xy的取值范围是:______________,(4) 的取值范围是:___________.典型例题3. 利用不等式的性质求取值范围例5. 已知函数f(x)=ax2-c,满足-4≤f(1)
≤-1,-1≤f(2)≤5,那么f(3)的取值范
围是______________.典型例题3. 利用不等式的性质求取值范围例5. 已知函数f(x)=ax2-c,满足-4≤f(1)
≤-1,-1≤f(2)≤5,那么f(3)的取值范
围是______________.拓展. 已知-1≤a+b≤5,-1≤a-b≤3,
求3a-2b的取值范围.典型例题4. 解一元二次不等式例6. 解不等式:
(1) 2x2+7x+4>0; (2) -x2+8x-3>0.典型例题4. 解一元二次不等式例7. 解关于x的不等式:(x-2) (ax-2)>0.典型例题4. 解一元二次不等式例8. 已知集合A={x| x2+2x-8<0},
B={x| x>1或x<-5},
C={x| x2-2mx+m2-1<0},
若(1) A∩C=?,(2) A∩B?C,分别求出
m的取值范围.典型例题4. 解一元二次不等式例9.已知关于x的方程(k-1)x2+(k+1)x+
k+1=0有两个相异实根,求实数k的取值
范围. 典型例题4. 解一元二次不等式例9.已知关于x的方程(k-1)x2+(k+1)x+
k+1=0有两个相异实根,求实数k的取值
范围. 变式.一根大于1,一根小于1,求实数k的
取值范围.三维设计<阶段质量检测>.课后作业湖南省长沙市一中卫星远程学校
及其解法二元一次不等式
(组)与平面区域基本
不等式简单的线性
规划问题最大(小)
值问题知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理1. 应用不等式(组)表示不等关系;
不等式的主要性质:(2)传递性:(3)加法法则:(4)乘法法则:(1)对称性:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理(6)乘方法则:(7)开方法则:(5)倒数法则:1. 应用不等式(组)表示不等关系;
不等式的主要性质:(一) 不等式与不等关系知识梳理2. 应用不等式的性质比较两个实数的大小
——作差法.3. 应用不等式性质证明.知识梳理(二) 一元二次不等式及其解法一元二次不等式的解集:设相应的一元二次方程的两根为x1,x2,且x1≤x2,则不等式的解的各种情况如下表:知识梳理yxO典型例题例1. 某电脑用户计划用不超过500元的资
金购买单价分别为60元、70元的单片软件
和盒装软件,根据需要,单片软件至少买
3片,盒装软件至少买2盒,写出满足上述
不等关系的不等式.1. 用不等式表示不等关系典型例题例2. 咖啡馆配制两种饮料,甲种饮料用奶
粉、咖啡、糖,分别为9g、4g、3g;乙种
饮料用奶粉、咖啡、糖,分别为4g、5g、
5g.已知每天使用原料为奶粉3600g,咖啡
2000g,糖3000g.写出配制两种饮料杯数所
满足的所有不等关系的不等式.1. 用不等式表示不等关系典型例题2. 比较大小例3. 典型例题2. 比较大小例3. < 典型例题2. 比较大小例3. < < 典型例题2. 比较大小例3. < < < 典型例题2. 比较大小例3. 典型例题2. 比较大小例3. < 典型例题2. 比较大小例3. < < 典型例题2. 比较大小例3. < < ≥典型例题3. 利用不等式的性质求取值范围例4. 如果30<x<42,16<y<24,则
480<xy<1008.
(1) x+y的取值范围是:___________,
(2) x-2y的取值范围是:___________,
(3) xy的取值范围是:______________,(4) 的取值范围是:___________.典型例题3. 利用不等式的性质求取值范围例5. 已知函数f(x)=ax2-c,满足-4≤f(1)
≤-1,-1≤f(2)≤5,那么f(3)的取值范
围是______________.典型例题3. 利用不等式的性质求取值范围例5. 已知函数f(x)=ax2-c,满足-4≤f(1)
≤-1,-1≤f(2)≤5,那么f(3)的取值范
围是______________.拓展. 已知-1≤a+b≤5,-1≤a-b≤3,
求3a-2b的取值范围.典型例题4. 解一元二次不等式例6. 解不等式:
(1) 2x2+7x+4>0; (2) -x2+8x-3>0.典型例题4. 解一元二次不等式例7. 解关于x的不等式:(x-2) (ax-2)>0.典型例题4. 解一元二次不等式例8. 已知集合A={x| x2+2x-8<0},
B={x| x>1或x<-5},
C={x| x2-2mx+m2-1<0},
若(1) A∩C=?,(2) A∩B?C,分别求出
m的取值范围.典型例题4. 解一元二次不等式例9.已知关于x的方程(k-1)x2+(k+1)x+
k+1=0有两个相异实根,求实数k的取值
范围. 典型例题4. 解一元二次不等式例9.已知关于x的方程(k-1)x2+(k+1)x+
k+1=0有两个相异实根,求实数k的取值
范围. 变式.一根大于1,一根小于1,求实数k的
取值范围.三维设计<阶段质量检测>.课后作业湖南省长沙市一中卫星远程学校
