1.2 应用举例
图片预览






文档简介
课件18张PPT。解斜三角形应用举例基础知识复习解斜三角形应用举例1、正弦定理2、余弦定理解斜三角形应用举例解应用题的一般步骤1.审题
理解题意,明确背景,熟悉已知条件,了解所需要的条件(或量),明确试题的所求内容.
2.建立数学模型
把实际问题转化为数学问题.
3.解答数学模型
解答数学问题.
4.总结
与问题所求量进行联系,总结作答. 斜三角形应用题的解题要点
解斜三角形的问题,通常都要根据题意,从实际问题中寻找
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
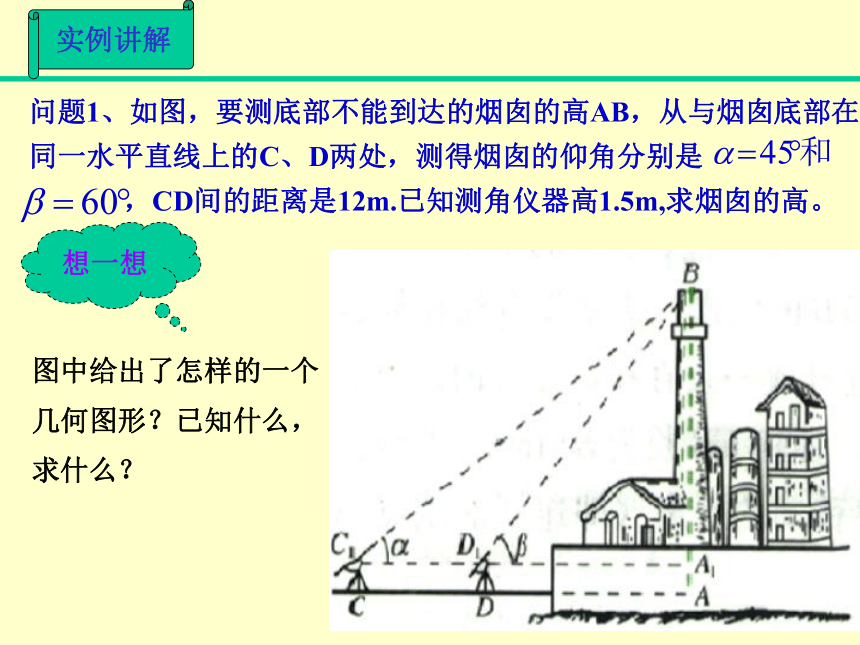
从而得到实际问题的解。解斜三角形应用举例实例讲解问题1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m. 本题解法二提示
亦可先设出A1B与A1D1的长分别为x和y,利用直角△BD1A1
与直角△BC1A1的边角的正切关系求解。问题2. 怎样测量一个底部不能到达的建筑物的高度?如图,在北京故宫的四个角上各矗立着一座角楼,如何通过测量,求得角楼的高度? 分析:如图,设线段AB表示角楼的高度,在宫墙外护城河畔的马路边,选位置C对角楼进行测量。 设CC’为测量仪器的高,过点C’的水平面与AB相交于点B’,这时由测点C’,可测得点A的仰角α的大小。在△AB’C’中,三条边的长度都无法测出,因而AB’无法求得。 如果移动测量仪CC’到DD’(测量仪高度不变),想想看,我们能测得哪些数据,使问题得以解决? 事实上,如图所示,在点B’,C’,D’构成的三角形中,可以测得∠β和∠γ的大小,又可测得B’C’的长。这样,我们就可以根据正弦定理求出边B’C’的长,从而求出AB’的长。使得问题得到解决。某校用自制的仪器,测得α=20°,β=99°,γ=45°,CD=60m,测量仪器的高是1.5m,试求出故宫角楼的高度。(精确到0.1米)解:在△B’C’D’中,由正弦定理得,因此 在△AB’C’中,
AB’=B’C’tanα
=72.17×tan20°
≈26.3m,
因此,AB=AB’+BB’
=26.3+1.5=27.8(m).
答:故宫角楼的高约为27.8m. 自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。练习讲解想一想实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.分析实例2、如图,一艘船以32.2 nmile/h的速度
向正北航行, 在A处看灯塔S在船的
北偏东 ,30min后航行到B处,在B
处看灯塔S在船的北偏东 方向上,
求灯塔S和B处的距离(精确到0.1nmile).第1题第2题3291m7.8 n mile实例讲解 例3. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).自我分析3、下图为曲柄连杠机构示意图,当曲柄OA在水平位置OB时,
连杠端点P在Q的位置 .当OA自OB按顺时针方向旋转角时,P和Q之间的距离是.已知OA=25cm,AP=125cm,分别求下列条件下的 值(精确到0.1cm)(1)(2)(3)(4)课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解
理解题意,明确背景,熟悉已知条件,了解所需要的条件(或量),明确试题的所求内容.
2.建立数学模型
把实际问题转化为数学问题.
3.解答数学模型
解答数学问题.
4.总结
与问题所求量进行联系,总结作答. 斜三角形应用题的解题要点
解斜三角形的问题,通常都要根据题意,从实际问题中寻找
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
从而得到实际问题的解。解斜三角形应用举例实例讲解问题1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m. 本题解法二提示
亦可先设出A1B与A1D1的长分别为x和y,利用直角△BD1A1
与直角△BC1A1的边角的正切关系求解。问题2. 怎样测量一个底部不能到达的建筑物的高度?如图,在北京故宫的四个角上各矗立着一座角楼,如何通过测量,求得角楼的高度? 分析:如图,设线段AB表示角楼的高度,在宫墙外护城河畔的马路边,选位置C对角楼进行测量。 设CC’为测量仪器的高,过点C’的水平面与AB相交于点B’,这时由测点C’,可测得点A的仰角α的大小。在△AB’C’中,三条边的长度都无法测出,因而AB’无法求得。 如果移动测量仪CC’到DD’(测量仪高度不变),想想看,我们能测得哪些数据,使问题得以解决? 事实上,如图所示,在点B’,C’,D’构成的三角形中,可以测得∠β和∠γ的大小,又可测得B’C’的长。这样,我们就可以根据正弦定理求出边B’C’的长,从而求出AB’的长。使得问题得到解决。某校用自制的仪器,测得α=20°,β=99°,γ=45°,CD=60m,测量仪器的高是1.5m,试求出故宫角楼的高度。(精确到0.1米)解:在△B’C’D’中,由正弦定理得,因此 在△AB’C’中,
AB’=B’C’tanα
=72.17×tan20°
≈26.3m,
因此,AB=AB’+BB’
=26.3+1.5=27.8(m).
答:故宫角楼的高约为27.8m. 自动卸货汽车的车箱采用液压机构。设计时需要计算油泵
顶杠BC的长度(如图所示)。已知车箱的最大仰角为 ,油
泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长(保留三个有效数
字)。练习讲解想一想实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.分析实例2、如图,一艘船以32.2 nmile/h的速度
向正北航行, 在A处看灯塔S在船的
北偏东 ,30min后航行到B处,在B
处看灯塔S在船的北偏东 方向上,
求灯塔S和B处的距离(精确到0.1nmile).第1题第2题3291m7.8 n mile实例讲解 例3. 图中是曲柄连杆机构示意图,当曲柄CB绕C点旋转时,通
过连杆AB的传递,活塞作直线往复运动,当曲柄在CB0位置时,曲
柄和连杠成一条直线,连杠的端点A在A0处。设连杠AB长为340
mm,曲柄CB长为85mm,曲柄自CB0按顺时针方向旋转80o,求活塞
移动的距离(即连杠的端点A移动的距离A0A)(精确到1mm).自我分析3、下图为曲柄连杠机构示意图,当曲柄OA在水平位置OB时,
连杠端点P在Q的位置 .当OA自OB按顺时针方向旋转角时,P和Q之间的距离是.已知OA=25cm,AP=125cm,分别求下列条件下的 值(精确到0.1cm)(1)(2)(3)(4)课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解
