1.2应用举例——角度问题

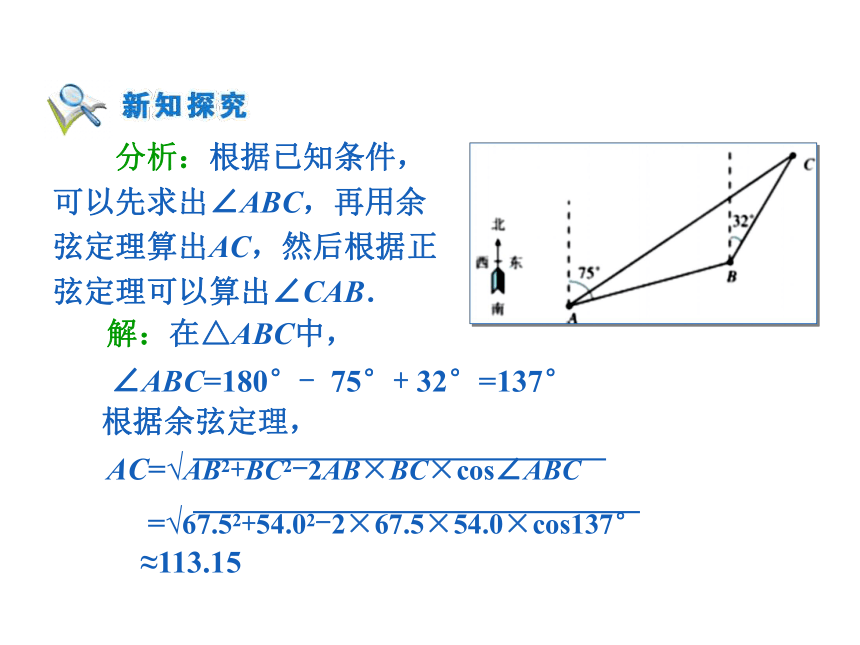
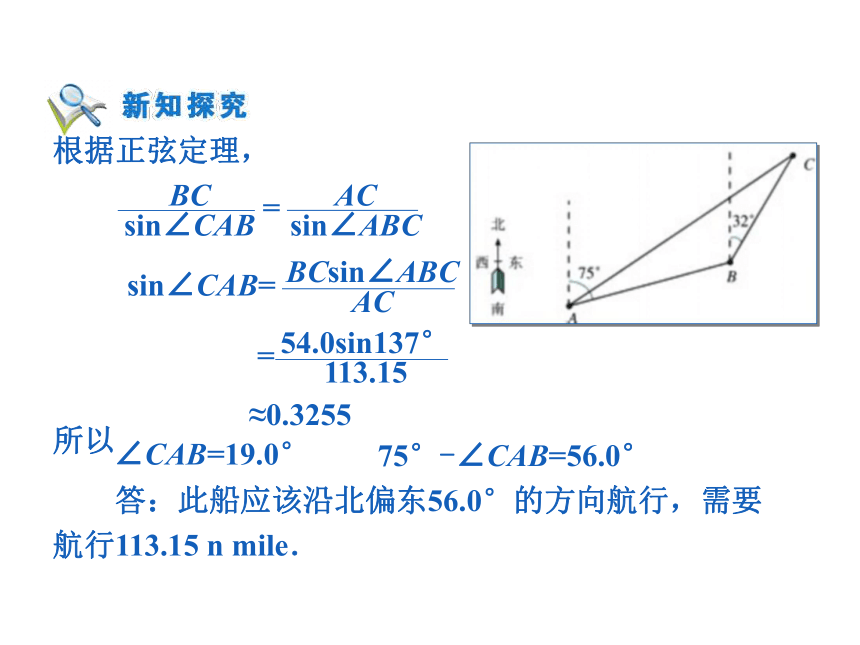
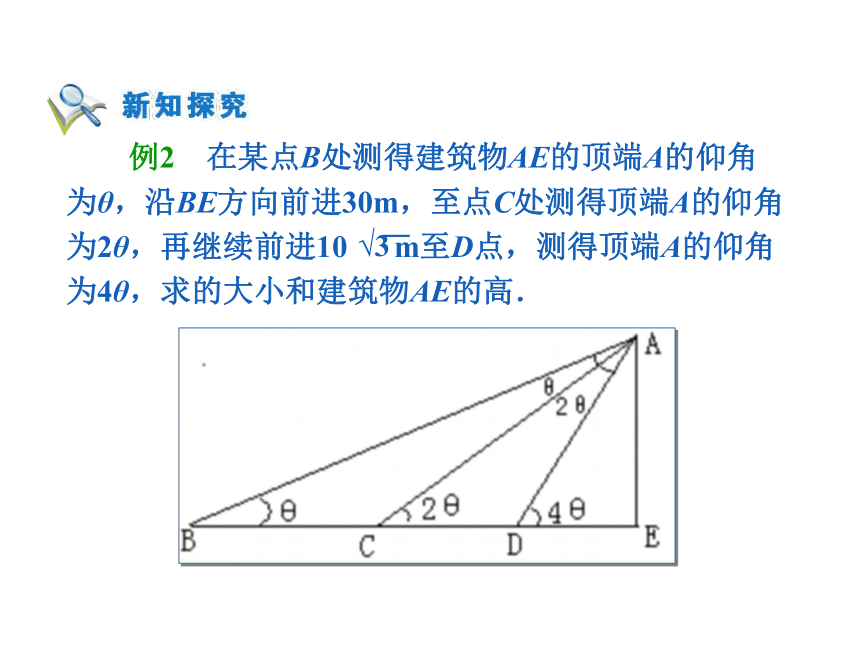
课件17张PPT。应用举例——角度问题　　在浩瀚无垠的海面上，要确保轮船不迷失方向，必须要能测出轮船的航速和航向，你能利用三角形的正弦定理和余弦定理进行测量吗？　　例1　如下图，一艘轮船从A出发，沿北偏东75°的方向航行67.5 n mile 后到达海岛B，然后从B出发，沿北偏东32°的方向航行54.0 n mile 后到达海岛C．如果下次航行直接从A出发到达C，此船应该沿怎样的方向航行，需要航行多少的距离？（角度精确到0.1°，距离精确到0.01 n mile）　　分析：根据已知条件，可以先求出∠ABC，再用余弦定理算出AC，然后根据正弦定理可以算出∠CAB．解：在△ABC中，根据余弦定理，≈113.15∠ABC=180°- 75°+ 32°=137°根据正弦定理，≈0.3255所以∠CAB=19.0°75°-∠CAB=56.0°　　答：此船应该沿北偏东56.0°的方向航行，需要航行113.15 n mile． 　　解：由已知可得，在△ACD中，因为 sin4θ=2sin2θcos2θ 根据正弦定理，得 2θ=30° θ=15°答：所求角θ为15°，建筑物高度为15m．　　例3　我舰在敌岛A南偏西50°相距12 海里的B处，发现敌舰正由岛北偏西10°的方向以10海里的速度航行．问我舰需以多大速度，沿什么方向航行才能用2小时追上敌舰？ 解：如图，在△ABC中由余弦定理得：BC2=AC2+AB2-2·AB·AC·cos∠BAC=202+122-2×12×20×cos120°=784BC=2828÷2=14（海里/小时）在△ABC中，由正弦定理得：B≈38.21°50°-38.21°=11.79°答：我舰的追击速度为14 海里/小时，舰行的方向为北偏东大约11.79° ．　　解三角形的应用题时，通常会遇到两种情况：　　（1）已知量与未知量全部集中在一个三角形中，依次利用正弦定理或余弦定理解之． 　　（2）已知量与未知量涉及两个或几个三角形，这时需要选择条件足够的三角形优先研究，再逐步在其余的三角形中求出问题的解． 　　在分析解决具体问题的过程中，关键要分析题意，分清已知与所求，根据题意画出示意图，并正确运用正弦定理和余弦定理解题．　　　　在解实际问题的过程中，贯穿了数学建模的思想，其流程图可表示为：数学模型的解画图形解三角形检验（答）数学模型实际问题的解实际问题　　1. 如图，3.5m长的棒斜靠在石堤旁，棒的一端在离堤足1.2m的地面上，另一端在沿堤上2.8m的地方．求堤对地面的倾斜角α．　　解：如右图，题目转化为已知△ABC的三条边，求α.由余弦定理的推论，可得≈-0.442∠ACB ≈116.23°α =180°-∠ACB≈180°-116.23°≈63.77°　　2 . 同步通讯卫星在赤道上空35800 km的轨道上，它每24小时绕地球一周，所以它定位于赤道上某一点的上空．如果此点与北京在同一条子午线上，北京的纬度是北纬39°54′，求在北京观察此卫星的仰角（取地球半径是6400km）？分析：根据题意，可以画出如下图形　　解：在△ABC中，根据余弦定理＝37515.44（km）≈-0.6924∠BAC ≈133.82°∠BAC-90°≈43.82°　　解：设经过t小时台风中心移动到Q点时，台风边沿恰经过O城，　　由题意可得：OP=300，PQ=20t，OQ=r(t)=60+10t由余弦定理可得：OQ2=OP2+PQ2-2·OP·PQ·cosα∴ t2-36t+288=0，解得t1=12，t2=24，t2-t1=12　　答：12小时后该城市开始受到台风侵袭，受到台风的侵袭时间有12小时．