2.1 数列的概念与简单表示法

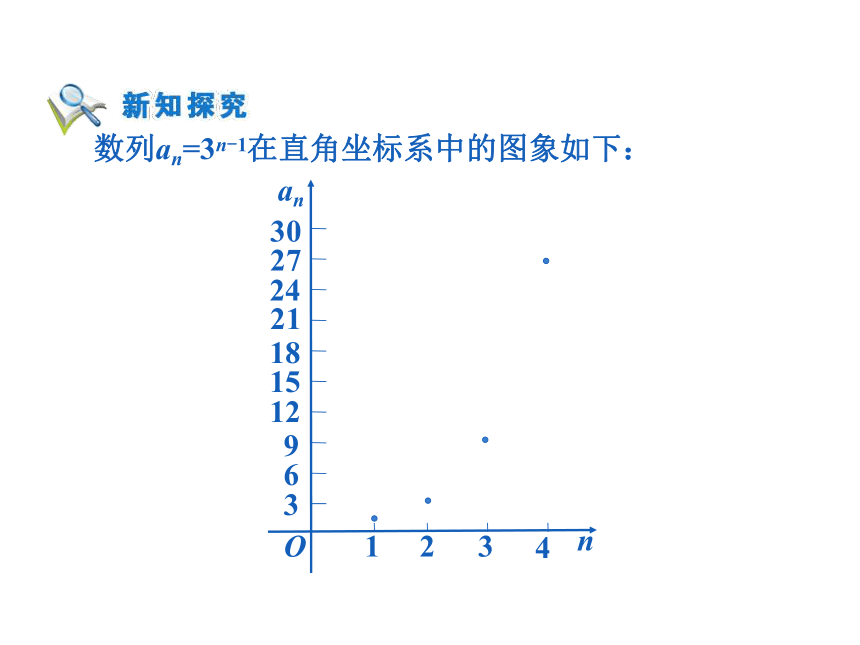
课件16张PPT。数列的简单表示　　复习：　　按照一定顺序排列着的一列数称为数列（sequence of number），数列中的每一个数叫做这个数列的项．　　如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．我们可以根据数列的通项公式写出数列．　　思考：　　通项公式可以看成数列的函数解析式．利用一个数列的通项公式，你能确定这个数列哪些方面的性质？　　例1　写出下面数列的一个通项公式，使它的前4项分别是下列各数：（2）2，0，2， 0；　　解：（1）这个数列的前4项的绝对值都是序号的倒数，并且奇数项为正，偶数项为负，所以，它的一个通项公式为：（2）2，0，2， 0；　　这个数列的前4项构成一个摆动数列，奇数项是2，偶数项是0，所以它的一个通项公式为：an=（-1）n+1+1如（1）也可以写作：或　　与函数一样，数列也可以用图象、列表等方法来表示．数列的图象是一系列孤立的点．例如，全体正偶数按从小到大的顺序构成数列2，4，6，…，2n，… .这个数列还可以用列表和图象分别表示在下表和下图中　　例2　下图中的三角形称为希尔宾斯基（Sierpinski）三角形．在下图4个三角形中，着色三角形的个数依次构成一个数列的前4项，请写出这个数列的一个通项公式，并在直角坐标系中画出它的图象．　　解：如图，这4个三角形中着色三角形的个数依次为1，3，9，27 ．则所求数列的前4项都是3的指数幂，指数为序号减1 ．所以，这个数列的一个通项公式是：an=3n-1数列an=3n-1在直角坐标系中的图象如下：　　如果一个数列{an}的首项a1=1，从第2项起的每一项等于它的前一项的2倍再加1，即an=2an-1+1（n＞1），那么a2=2a1+1=3，a3=2a2+1=7，…像这样给出数列的方法叫做递推法，其中an=2an-1+1（n＞1）称为递推公式．递推公式也是数列的一种表示方法．　　例3　设数列{an}满足写出这个数列的前5项．解：由题意可知a1=1，1．根据数列的通项公式填表：21336912　　2．观察下面数列的特点，用适当的数填空，并写出各数列的一个通项公式： (1)　（ ），-4，9，（ ），25，（ ），49；1-16-36an=（-1）n+1n2　　3．已知数列{an}满足a1=1，an=an-12-1（n＞1），写出它的前5项．解：由题意可知a1=1，a2=a12-1=12-1=0，a3=a22-1=02-1=-1，a4=a32-1=（-1）2-1=0，a5=a42-1=02-1=-1．　　4．数列的前5项分别是以下各数，写出各数列的一个通项公式：　　1．中国银行人民币活期存款年利率为0.72％ ．假设某人存入10万元人民币后，既不加进存款也不取钱，每年到期利息连同本金自动转存．如果不考虑利息税，用an表示第n年到期时的存款余额，求a1，a2，a3及an ．解：根据题意， a2=10×（1+0.72％）2≈10.144518； a3=10×（1+0.72％）3≈10.217559； an=10×（1+0.72％）n ．a1=10×（1+0.72％）=10.072；　　2．已知数列{an}的第1项是1，第2项是2，以后各项由，an=an-1+an-2（n＞2）给出．（1）写出这个数列的前5项；解：（1）根据题意，可得数列{an}为：1，2，3，5，8