等差数列的前n项和(一)
图片预览






文档简介
课件16张PPT。高斯(Gauss, Carl Friedrich, 1777-1855)
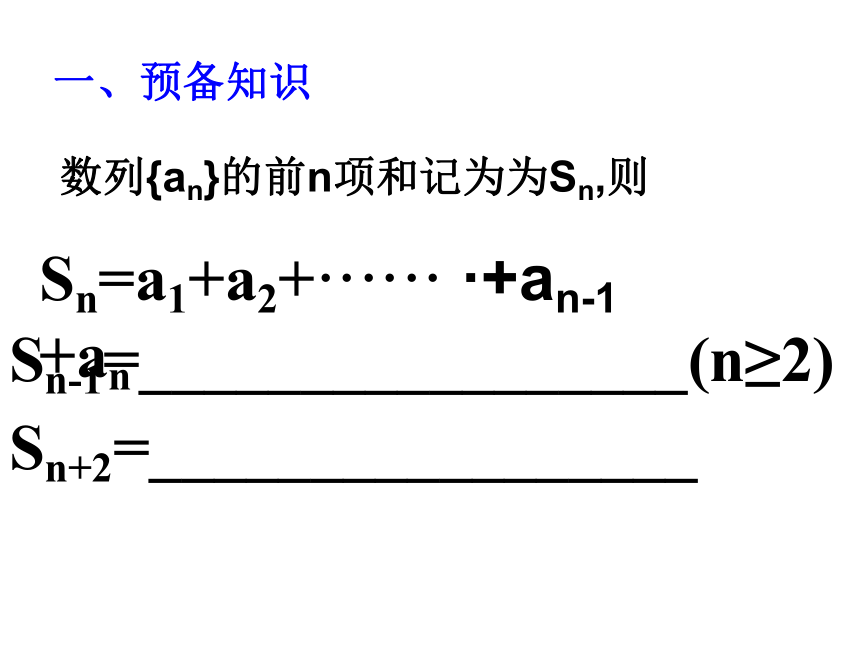
德国数学家、物理学家、天文学家。1777年4月30日生于不伦瑞克,1855年2月23日卒于格丁根。高斯是近代 数学奠基者之一. 与阿基米德、牛顿号称”三大数学大师”,并享有”数学王子”的美誉!他幼年时就 表现出超人的数学天才。等差数列的前n项和(一)浏阳市田家炳实验中学一、预备知识数列{an}的前n项和记为为Sn,则Sn=a1+a2+······ ·+an-1 +anSn-1=_________________(n≥2)Sn+2=_________________1.复习等差数列的概念
等差数列的定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差 等于同一常数,这个数列就叫做等差数列,这个常数叫做等差数列的公差(用字母d来表示)
或者是:对于数列{an},若an+1-an=d (常数)(n∈N*),则这个数列就叫做等差数列,常数d叫公差。
a2-a1=a3-a2=…=an+1-an=d
二、备用知识速递2.等差数列的通项公式: 3.等差数列{an}的性质
①若m、n、p、q∈N*且m+n=p+q 则 ______________当p=q时,am+an=2ap) ② a1+an=a2+an-1=a3+an-2=…1.伟大的数学家高斯十岁时,一天上数学课老师出了一道题目:1+2+…+100=?其他同学忙用笔在纸上计算,而小高斯确很快求出了他的结果。后人称为 “高斯算法”
你知道小高斯是如何计算的吗?三、新课引入高斯算法1+2+3+······+100=?首项与末项的和: ____________第2项与倒数第2项的和: _____________ 第3项与倒数第3项的和: ______________? · · · · · · 第50项与倒数第50项的和:_____________于是所求的和是: 101×50=_________1:推导公式,识记公式
1):由1+2+3+……+100==5050若将其中的100换成n,可以得到S100=三:新课讲授2:公式的推导“倒序相加”法(1)Sn= a1 + a2 + a3 +…+ an-2+ an-1+ anSn= an+ an-1+ an-2+…+ a3 + a2 + a1 课堂小练1. 根据下列条件,求相应的等差数列 的4:公式的变形(2)5:公式巩固与简单应用
(1)求等差数列 2,4,6,8,10, …前n项的和.
(2)在等差数列{an}中 a1=-50 , d=-2 求 S10
(3)在等差数列{an}中,a1=10,d=-2,求Sn+1
(4)在等差数列{an}中,a1=-10,d=4,Sn=80,求n
例1:一个社会学家对城镇子女的培养成本作了调查,得出这样的结论:一个小孩从3岁起,第一年须支付3000元,以后每年在前一年的基础上增加500元.试计算当孩子大学毕业(22岁),家庭共要支付多少元?四:例题讲解例2:等差数列{an}中,已知a4+a13=4,求S16的值。变式(2) :等差数列{an}中,已知a12=10,求S23的值。若m、n、p、q∈N*且m+n=p+q 则 am+an=ap+aq(当p=q时,am+an=2ap)变式(1) :等差数列{an}中,已知a9=8,求S17的值。1.一种方法:_______________
2.两个公式:_______________
________________五:课堂小结4.两种思想:“方程的思想”与“整体代换的思想”。3.一个结论:____________________课后作业:课本习题2.3? A组 1, 2, 3Bye Bye !祝同学们学习愉快,人人成绩优异!
等差数列的定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差 等于同一常数,这个数列就叫做等差数列,这个常数叫做等差数列的公差(用字母d来表示)
或者是:对于数列{an},若an+1-an=d (常数)(n∈N*),则这个数列就叫做等差数列,常数d叫公差。
a2-a1=a3-a2=…=an+1-an=d
二、备用知识速递2.等差数列的通项公式: 3.等差数列{an}的性质
①若m、n、p、q∈N*且m+n=p+q 则 ______________当p=q时,am+an=2ap) ② a1+an=a2+an-1=a3+an-2=…1.伟大的数学家高斯十岁时,一天上数学课老师出了一道题目:1+2+…+100=?其他同学忙用笔在纸上计算,而小高斯确很快求出了他的结果。后人称为 “高斯算法”
你知道小高斯是如何计算的吗?三、新课引入高斯算法1+2+3+······+100=?首项与末项的和: ____________第2项与倒数第2项的和: _____________ 第3项与倒数第3项的和: ______________? · · · · · · 第50项与倒数第50项的和:_____________于是所求的和是: 101×50=_________1:推导公式,识记公式
1):由1+2+3+……+100==5050若将其中的100换成n,可以得到S100=三:新课讲授2:公式的推导“倒序相加”法(1)Sn= a1 + a2 + a3 +…+ an-2+ an-1+ anSn= an+ an-1+ an-2+…+ a3 + a2 + a1 课堂小练1. 根据下列条件,求相应的等差数列 的4:公式的变形(2)5:公式巩固与简单应用
(1)求等差数列 2,4,6,8,10, …前n项的和.
(2)在等差数列{an}中 a1=-50 , d=-2 求 S10
(3)在等差数列{an}中,a1=10,d=-2,求Sn+1
(4)在等差数列{an}中,a1=-10,d=4,Sn=80,求n
例1:一个社会学家对城镇子女的培养成本作了调查,得出这样的结论:一个小孩从3岁起,第一年须支付3000元,以后每年在前一年的基础上增加500元.试计算当孩子大学毕业(22岁),家庭共要支付多少元?四:例题讲解例2:等差数列{an}中,已知a4+a13=4,求S16的值。变式(2) :等差数列{an}中,已知a12=10,求S23的值。若m、n、p、q∈N*且m+n=p+q 则 am+an=ap+aq(当p=q时,am+an=2ap)变式(1) :等差数列{an}中,已知a9=8,求S17的值。1.一种方法:_______________
2.两个公式:_______________
________________五:课堂小结4.两种思想:“方程的思想”与“整体代换的思想”。3.一个结论:____________________课后作业:课本习题2.3? A组 1, 2, 3Bye Bye !祝同学们学习愉快,人人成绩优异!
