2.5 等比数列的前n项和
图片预览








文档简介
课件20张PPT。等比数列的前n项和1、等比数列的定义:
2、通项公式:
3、数列中通项与前n项和的关系: 回顾创设情境 从前有一个人卖马,标价3000元.有个买主嫌贵.卖主对他说:“如果你能改买马蹄子上的钉子,我就把马送给你.”买主便问怎么个卖法.卖主讲,4只马蹄子上共有24个钉子,第1个钉子卖1分钱,第2个钉子卖2分钱,第3个钉子卖4分钱,依次类推,即后一个钉子是前一个钉子价钱的2倍.买主听后心动了,认为买24个钉子花不了几个钱.
他真的花不了几个钱吗?请大家先看一个故事本故事源自意大利一古代数学手稿它是以1为首项公比是2的等比数列. 由于每一个钉子的价钱都是前一个钉子的2倍,共有24个钉子, 每个钉子的价钱依次为:买24个钉子要花的钱为: (单位:分)分析:这是一个求等比数列前n项和的问题!探求等比数列求和的方法问题:已知等比数列 , 公比为q,
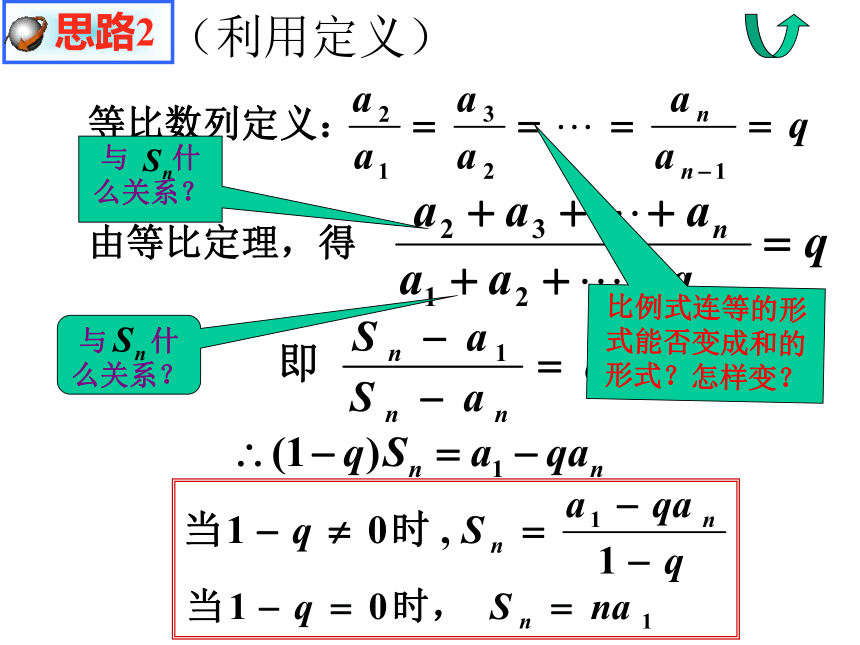
求:思考:思路1思路2思路3公式(错位相减法)当q≠1时两式相减,得当q=1时,Sn=?此式相邻两项有何关系?当q=1时 思路1(利用定义)由等比定理,得等比数列定义:与 什么关系?与 什么关系?比例式连等的形式能否变成和的形式?怎样变? 思路2(利用 ) 思路3等比数列前n 项和公式公式2:公式1:根据求和公式,运用方程思想, 五个基本量中“知三求二”. 注意对 是否等于 进行分类讨论【例1】求“卖马的故事”中要买24个钉子的价钱〔解〕=16777215(分)=167772.15(元)≈16.7(万元)怎么会这么多?!涓涓细流,汇成江河.分分秒秒,铸就成功. 例题【例2】求等比数列 的前8项的和.解:【例3】解法1:②①③③代入②得代入③得:n=5.解法2〔分析〕 (建立数列模型)从第1年起,每年销售量分别为:本题实质上是已知前n项和,求项数n的问题.构成等比数列.某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1年起,约几年内可使总销售量达到30000台(保留到个位)?【例4】〔解〕 由题知,从第1年起,每年的销售量组成一个等比数列代入等比数列前n 项和公式两边取对数得用计算器算得答: 约 5 年内可以使总销量达到30000台. 练习1. 根据下列条件,求相应的等比数列 的 练习练习2. 求等比数列 1,2,4,…从第5项到第10项的和. 从第5项到第10项的和: 求等比数列 从第3项到第7项的和. 从第3项到第7项的和:练习3.1、求和公式当q≠1时,当q=1时,①注意分类讨论的思想!
等比数列求和时必须弄清q=1还是q≠1.②运用方程的思想,五个量“知三求二”.2、公式的推导方法 强调:(重在过程)③注意运用整体运算的思想. 小结 作业课本69页A组1、2、3、4、 5、6
2、通项公式:
3、数列中通项与前n项和的关系: 回顾创设情境 从前有一个人卖马,标价3000元.有个买主嫌贵.卖主对他说:“如果你能改买马蹄子上的钉子,我就把马送给你.”买主便问怎么个卖法.卖主讲,4只马蹄子上共有24个钉子,第1个钉子卖1分钱,第2个钉子卖2分钱,第3个钉子卖4分钱,依次类推,即后一个钉子是前一个钉子价钱的2倍.买主听后心动了,认为买24个钉子花不了几个钱.
他真的花不了几个钱吗?请大家先看一个故事本故事源自意大利一古代数学手稿它是以1为首项公比是2的等比数列. 由于每一个钉子的价钱都是前一个钉子的2倍,共有24个钉子, 每个钉子的价钱依次为:买24个钉子要花的钱为: (单位:分)分析:这是一个求等比数列前n项和的问题!探求等比数列求和的方法问题:已知等比数列 , 公比为q,
求:思考:思路1思路2思路3公式(错位相减法)当q≠1时两式相减,得当q=1时,Sn=?此式相邻两项有何关系?当q=1时 思路1(利用定义)由等比定理,得等比数列定义:与 什么关系?与 什么关系?比例式连等的形式能否变成和的形式?怎样变? 思路2(利用 ) 思路3等比数列前n 项和公式公式2:公式1:根据求和公式,运用方程思想, 五个基本量中“知三求二”. 注意对 是否等于 进行分类讨论【例1】求“卖马的故事”中要买24个钉子的价钱〔解〕=16777215(分)=167772.15(元)≈16.7(万元)怎么会这么多?!涓涓细流,汇成江河.分分秒秒,铸就成功. 例题【例2】求等比数列 的前8项的和.解:【例3】解法1:②①③③代入②得代入③得:n=5.解法2〔分析〕 (建立数列模型)从第1年起,每年销售量分别为:本题实质上是已知前n项和,求项数n的问题.构成等比数列.某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1年起,约几年内可使总销售量达到30000台(保留到个位)?【例4】〔解〕 由题知,从第1年起,每年的销售量组成一个等比数列代入等比数列前n 项和公式两边取对数得用计算器算得答: 约 5 年内可以使总销量达到30000台. 练习1. 根据下列条件,求相应的等比数列 的 练习练习2. 求等比数列 1,2,4,…从第5项到第10项的和. 从第5项到第10项的和: 求等比数列 从第3项到第7项的和. 从第3项到第7项的和:练习3.1、求和公式当q≠1时,当q=1时,①注意分类讨论的思想!
等比数列求和时必须弄清q=1还是q≠1.②运用方程的思想,五个量“知三求二”.2、公式的推导方法 强调:(重在过程)③注意运用整体运算的思想. 小结 作业课本69页A组1、2、3、4、 5、6
