3.4基本不等式1

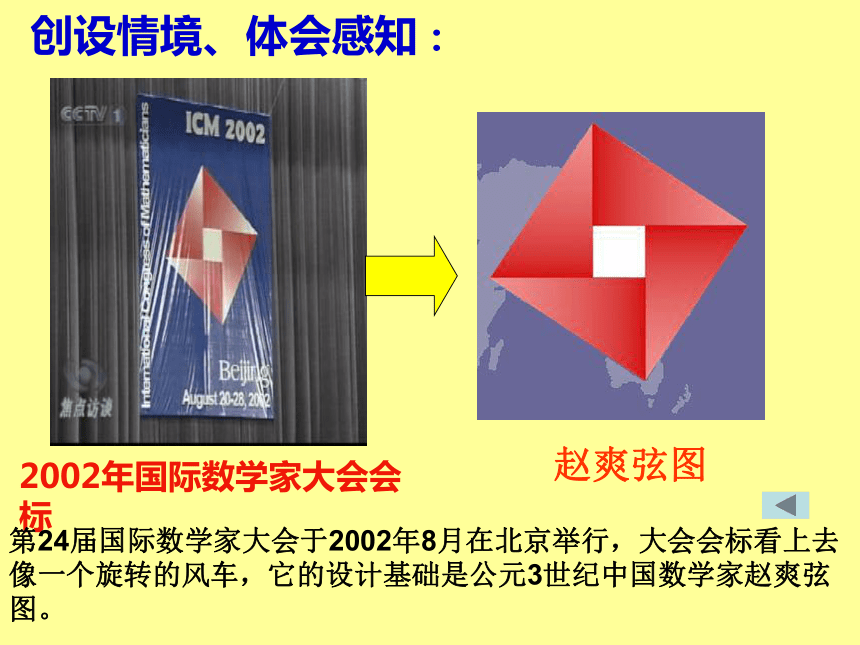
课件15张PPT。§3.4基本不等式2002年国际数学家大会会标 创设情境、体会感知：第24届国际数学家大会于2002年8月在北京举行，大会会标看上去
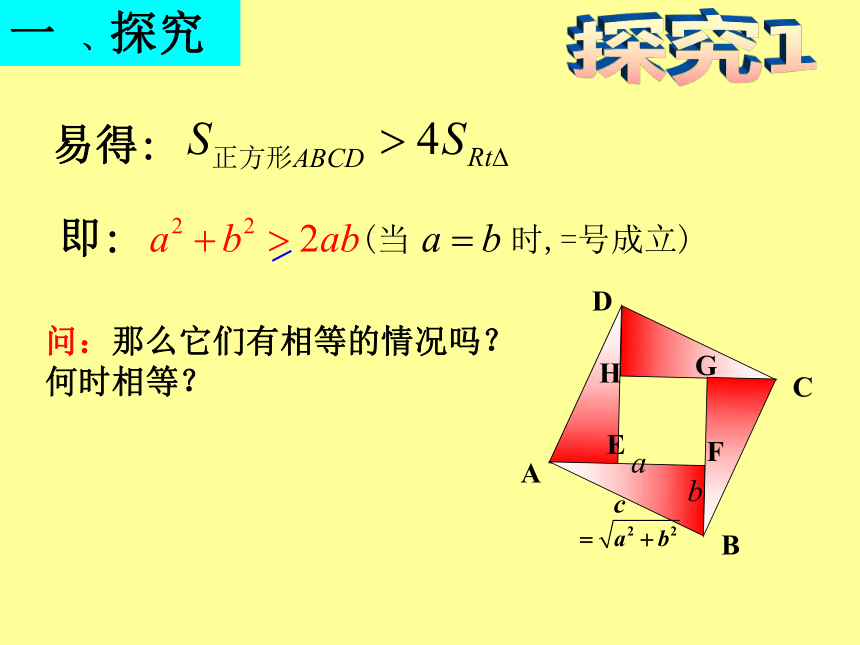
像一个旋转的风车，它的设计基础是公元3世纪中国数学家赵爽弦图。赵爽弦图探究1ADCBHGFE
问：那么它们有相等的情况吗？
何时相等？一 、探究易得:即:(当 时,=号成立)证明:综合(1),(2),得注意:2.代数意义：几何平均数小于等于算术平均数代数证明:3.几何意义：半弦长小于等于半径（当且仅当a=b时，等号成立）二、新课讲解几何证明:从数列角度看:两个正数的等比中项小于等于它们的等差中项1.思考:如果当 用 去替换
中的 ,能得到什么结论? 基本不等式证明:(1)换元法(2)作差法
(3)分析法
要证 ①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
显然,④是成立的.当且仅当a=b时, ④中的等号成立. 两个正数的算术平均数
不小于它们的几何平均数 注意:（当且仅当a=b时，等号成立）例1:证明:证明:(1)用篱笆围一个面积为　　的矩形菜园, 问该矩形的长、宽各为多少时, 所用篱笆最短，最短的篱笆是多少?(2).一段长为36m的篱笆围成一个矩形菜园，问这个矩形的长，宽各为多少时，菜园的面积最大，最大面积是多少？结论1：两个正数积为定值，则和有最小值结论2：两个正数和为定值，则积有最大值例2:练习