椭圆的简单几何性质

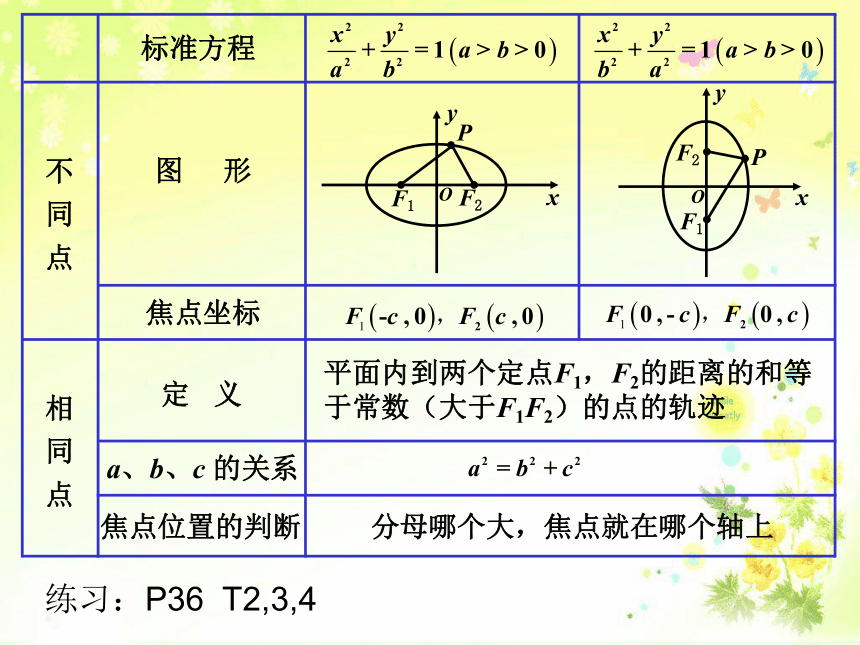
课件14张PPT。椭圆的简单几何性质分母哪个大，焦点就在哪个轴上平面内到两个定点F1，F2的距离的和等
于常数（大于F1F2）的点的轨迹练习：P36 T2,3,41、求满足下列椭圆的标准方程：
（1）过点(2,3)，且与椭圆9x2+4y2=36有共同的焦点。
（2）a+c=10，b2=40。练习：思维挑战题：
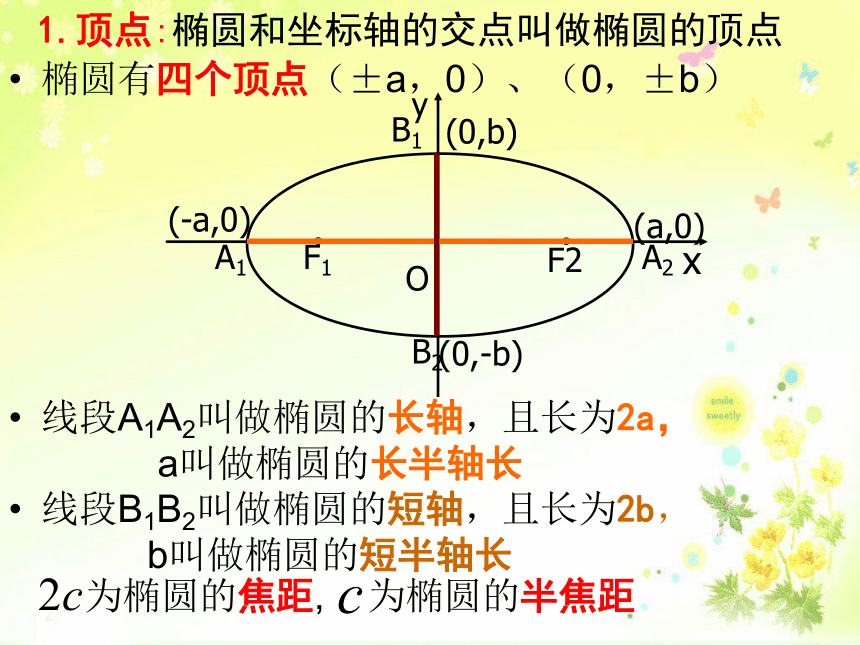
如图,已知圆B：(x+1)2+y2=16,及点A(1,0)，C为圆B上任一点，求AC的垂直平分线与线段BC的交点P的轨迹方程.1.顶点:椭圆和坐标轴的交点叫做椭圆的顶点椭圆有四个顶点（±a，0）、（0，±b）
线段A1A2叫做椭圆的长轴，且长为2a，
a叫做椭圆的长半轴长
线段B1B2叫做椭圆的短轴，且长为2b，
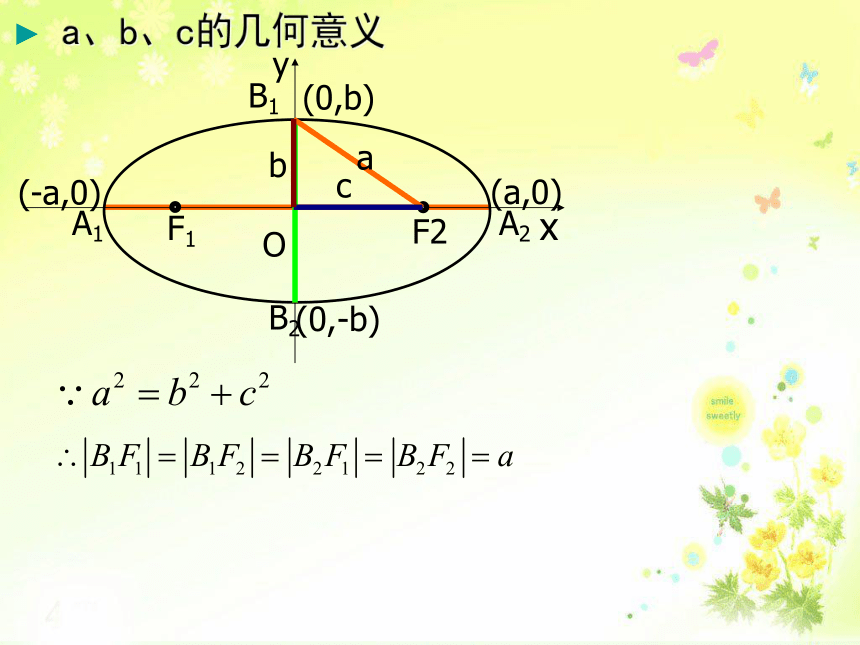
b叫做椭圆的短半轴长O x F1 F2 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) 为椭圆的焦距, 为椭圆的半焦距O x F1 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) a、b、c的几何意义a c b F2 -a≤x≤a, -b≤y≤b 知
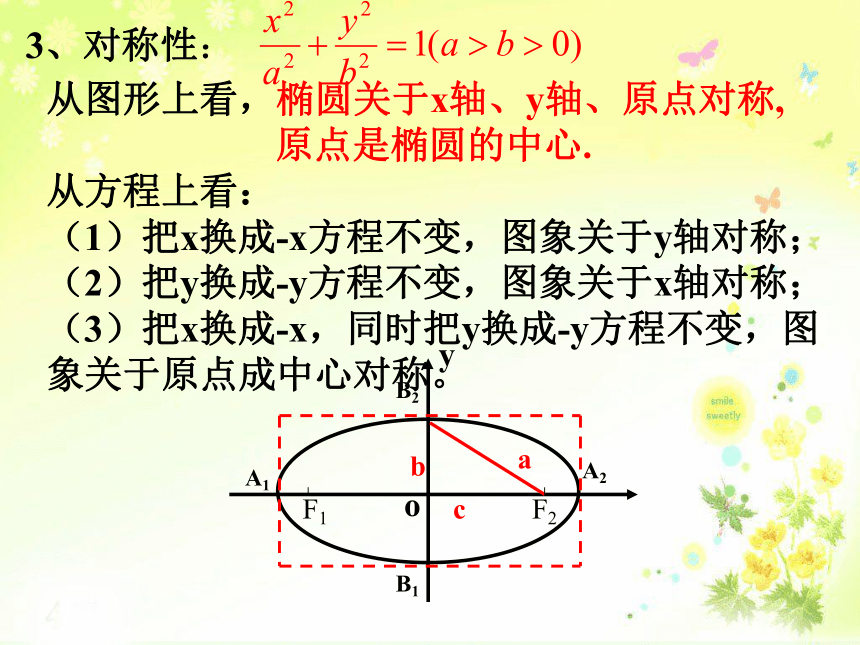
椭圆落在x=±a,y= ± b组成的矩形中2、范围：3、对称性：从图形上看，椭圆关于x轴、y轴、原点对称,
原点是椭圆的中心.
从方程上看：
（1）把x换成-x方程不变，图象关于y轴对称；
（2）把y换成-y方程不变，图象关于x轴对称；
（3）把x换成-x，同时把y换成-y方程不变，图象关于原点成中心对称。根据前面所学有关知识画出下列图形（1）（2）A1 B1 A2 B2 B2 A2 B1 A1 4、椭圆的离心率 (刻画椭圆扁平程度的量)椭圆的焦距与长轴长的比 叫做椭圆的离心率。[1]离心率的取值范围：[2]离心率对椭圆形状的影响：0当e＝1时曲线又是 什么？1）e越接近1，c就越接近a，从而b
就越小，椭圆就越扁
2）e越接近0，c就越接近0，从而b
就越大，椭圆就越圆圆线段F1F2两种标准方程的椭圆性质的比较关于x轴、y轴、原点对称A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)例1求椭圆16x2＋25y2＝400的长轴和短轴长，离心率，焦点和顶点坐标。解：把已知方程化为标准方程椭圆的四个顶点是A1(－5,0)、A2(5,0)、
B1(0,－4)、B2(0,4) 离心率焦点F1(－3,0)和F2(3,0),因此长轴长 ，短轴长 练习：P41 T2例2：求适合下列条件的椭圆的标准方程
⑴经过点P(－3,0)、Q(0,－2)；
⑵长轴长等于20，离心率3/5。
（1）解：利用椭圆的几何性质，以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点，于是焦点在x轴上，且点P、Q分别是椭圆长轴与短轴的一个端点，故a＝3，b＝2，故椭圆的标准方程为 练习：P42 T5例3：点M（x，y）与定点F(4,0)的距离和它到直线 的距离的比是常数 ，求点M的轨迹。练习：P43 T2练：已知x轴上的一定点A（1,0），Q为椭圆 上的动点，求AQ中点M的轨迹方程.-2解：设动点M的坐标为(x,y)，则Q的坐标为(2x-1,2y) 因为Q点为椭圆 上的点 所以点M的轨迹方程是