抛物线的定义与标准方程
图片预览






文档简介
课件19张PPT。抛物线及其标准方程例:点M(x,y)与定点F(4,0)
的距离和它到直线 的距离
的比是常数 ,求点M的轨迹。F(c,0)交叉相乘,平方,化简得:交叉相乘,平方,化简得: 平面内,到定点F的距离和到定直线L(F L)的
距离之比等于常数e(0 其中定点F就是椭圆的一个焦点,e就是其离心率,
定直线L叫做椭圆的准线。
依据椭圆的对称性,椭圆有两条准线.椭圆的第二定义解:设M(x,y),例:求与定点 及定直线 的距离的
比是定值 的动点M的轨迹方程。解:设M(x,y),双曲线的第二定义 平面内,到定点F的距离和到定直线L(F L)的
距离之比等于常数e(e>1)的点的轨迹是双曲线。
其中定点F就是双曲线的一个焦点,e就是其离心率,
定直线L叫做双曲线的准线。
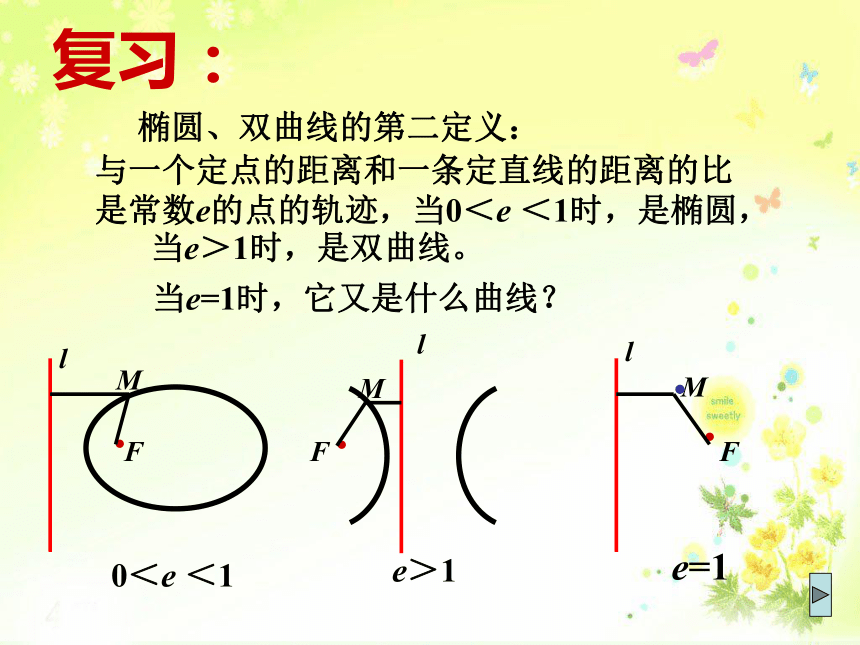
依据双曲线的对称性,双曲线有两条准线.F1F2xyA1A2OF2复习:椭圆、双曲线的第二定义:与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当0<e <1时,是椭圆,当e>1时,是双曲线。当e=1时,它又是什么曲线?平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义二、标准方程如何建立直角
坐标系?想一想二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知, 方程 y2 = 2px(p>0)叫做
抛物线的标准方程。其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。例2、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
例3、M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是x = ;(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y2、求下列抛物线的焦点坐标和焦点坐标:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2抛物线的画法数学这门学科不仅需要观察,还需要实验。(欧拉语)向右
向左
向上
向下
的距离和它到直线 的距离
的比是常数 ,求点M的轨迹。F(c,0)交叉相乘,平方,化简得:交叉相乘,平方,化简得: 平面内,到定点F的距离和到定直线L(F L)的
距离之比等于常数e(0
定直线L叫做椭圆的准线。
依据椭圆的对称性,椭圆有两条准线.椭圆的第二定义解:设M(x,y),例:求与定点 及定直线 的距离的
比是定值 的动点M的轨迹方程。解:设M(x,y),双曲线的第二定义 平面内,到定点F的距离和到定直线L(F L)的
距离之比等于常数e(e>1)的点的轨迹是双曲线。
其中定点F就是双曲线的一个焦点,e就是其离心率,
定直线L叫做双曲线的准线。
依据双曲线的对称性,双曲线有两条准线.F1F2xyA1A2OF2复习:椭圆、双曲线的第二定义:与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当0<e <1时,是椭圆,当e>1时,是双曲线。当e=1时,它又是什么曲线?平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义二、标准方程如何建立直角
坐标系?想一想二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知, 方程 y2 = 2px(p>0)叫做
抛物线的标准方程。其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;
(3)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。例2、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
例3、M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是x = ;(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y2、求下列抛物线的焦点坐标和焦点坐标:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2抛物线的画法数学这门学科不仅需要观察,还需要实验。(欧拉语)向右
向左
向上
向下
