圆锥的体积(课件)人教版数学六年级下册(共19张PPT)
文档属性
| 名称 | 圆锥的体积(课件)人教版数学六年级下册(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 550.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 21:14:27 | ||
图片预览






文档简介
(共19张PPT)
圆锥的体积
工地上有一堆沙子,这堆沙子的体积大约是多少?
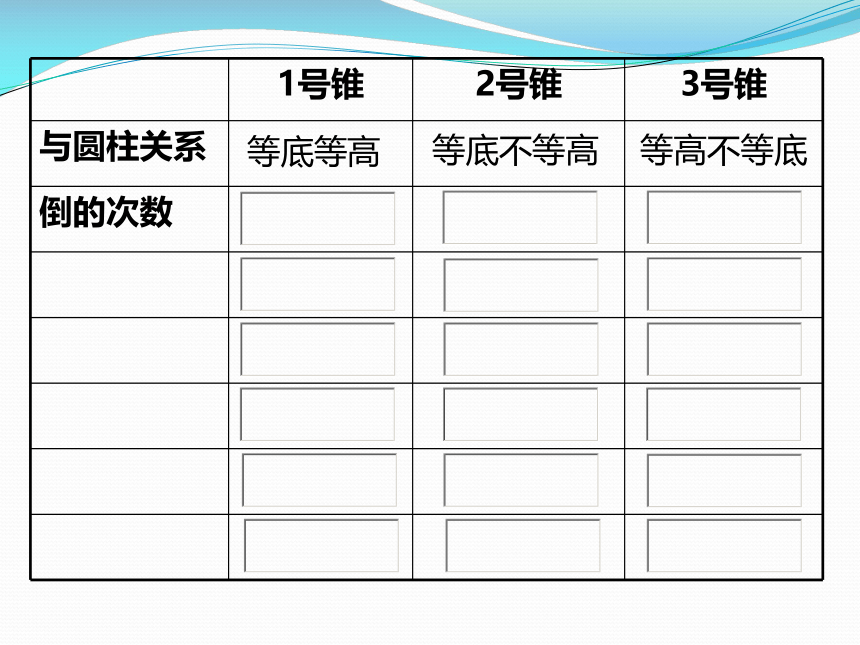
1号锥 2号锥 3号锥
与圆柱关系
倒的次数
等底等高
等底不等高
等高不等底
实验要求及说明:
1、将圆锥盛满沙子,沙子的体积就
视为圆锥的体积(器壁厚度不计) 。
2、将圆锥盛满沙子,多余的用直尺刮
掉,倒入圆柱,记录下倒的次数。
3、小组内分工合作完成实验,选出
一人汇报。
1号锥 2号锥 3号锥
与圆柱关系
倒的次数
等底等高
等底不等高
等高不等底
通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥= V圆柱= Sh
1、圆锥的体积=( ),用字母表示是
( )。
2、圆柱体积的 与和它( )的圆锥的体积相等。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是27立方
分米,圆锥的体积是( )立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积
是( )立方厘米。
3
1
等底等高
×底面积×高
V= sh
9
24
一、填空:
二、判断:
1、圆柱体体积一定比圆锥体的体积大 ( )
2、圆锥的体积等于和它等底等高的圆柱体的
( )
3、正方体、长方体、圆锥体的体积都等于底面
积×高。( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积
是9立方米,那么圆锥的体积是27立方米。
( )
√
×
×
×
三、填表:
已 知 条 件 体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
看谁最细心
工地上有一堆沙子,这堆沙子的体积大约是多少立方米?(保留2位小数)
4m
1.5m
如果每立方米沙1.5吨,这堆沙大约有多少吨?
(2)沙堆的体积:
(1)沙堆的底面积:
5.024×1.5=7.536(t)
(3)沙堆重:
答:这堆沙子大约重7.536吨。
(4÷2)2×3.14=12.56(m2)
×12.56×1.2 = 5.024(m3)
一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V圆锥= Sh
=
×19 ×12=76(cm )
答:这个零件的体积是76cm 。
2.如右图,一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高是6cm。每立方厘米钢大约重7.9g。这个铅锤大约重多少克 (得数保留整数。)
(2)铅锤的体积:
(1)铅锤的底面积:
25.12×7.9=198.448 ≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198克 。
×12.56×6=25.12(cm3)
(4÷2)2×3.14=12.56 (cm2)
3.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
= ×3.14×(31.4÷3.14÷2)2×9
= 235.5(cm3)
1
3
V = π( )2h
2π
C
答:它的体积是235.5cm3。
4.把一个圆锥沿着高切开,得到两个如图所示的图形,表面积增加了24 cm2。圆锥的高是6 cm,那么圆锥的体积是多少立方厘米?
5.有一个圆锥形沙堆,底面周长是9.42 m,高是1.5 m。如果将这些沙子铺在一个长6 m,宽2 m的长方体沙坑里,大约能铺多少厘米厚?(得数保留整数)
6.一个底面直径是16 cm的圆柱形容器中装有一些水,把一个底面半径是5 cm的圆锥形铁块完全浸没在水中,水未溢出,容器内的水上升了2.5 cm,圆锥形铁块的高是多少厘米?
3.14×(16÷2)2×2.5×3÷(3.14×52)=19.2(cm)
答:圆锥形铁块的高是19.2 cm。
这节课
你有什么收获?
2. 圆锥的体积公式用字母表示为V= Sh或
V= πr h。
3. 当已知圆锥的底面周长和高,可利用公式
来计算圆锥的体积。
1. 圆锥的体积等于与它等底等高的圆柱体积的 。
圆锥的体积
工地上有一堆沙子,这堆沙子的体积大约是多少?
1号锥 2号锥 3号锥
与圆柱关系
倒的次数
等底等高
等底不等高
等高不等底
实验要求及说明:
1、将圆锥盛满沙子,沙子的体积就
视为圆锥的体积(器壁厚度不计) 。
2、将圆锥盛满沙子,多余的用直尺刮
掉,倒入圆柱,记录下倒的次数。
3、小组内分工合作完成实验,选出
一人汇报。
1号锥 2号锥 3号锥
与圆柱关系
倒的次数
等底等高
等底不等高
等高不等底
通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥= V圆柱= Sh
1、圆锥的体积=( ),用字母表示是
( )。
2、圆柱体积的 与和它( )的圆锥的体积相等。
3、一个圆柱和一个圆锥等底等高,圆柱的体积是27立方
分米,圆锥的体积是( )立方分米。
4、一个圆锥的底面积是12平方厘米,高是6厘米,体积
是( )立方厘米。
3
1
等底等高
×底面积×高
V= sh
9
24
一、填空:
二、判断:
1、圆柱体体积一定比圆锥体的体积大 ( )
2、圆锥的体积等于和它等底等高的圆柱体的
( )
3、正方体、长方体、圆锥体的体积都等于底面
积×高。( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积
是9立方米,那么圆锥的体积是27立方米。
( )
√
×
×
×
三、填表:
已 知 条 件 体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
看谁最细心
工地上有一堆沙子,这堆沙子的体积大约是多少立方米?(保留2位小数)
4m
1.5m
如果每立方米沙1.5吨,这堆沙大约有多少吨?
(2)沙堆的体积:
(1)沙堆的底面积:
5.024×1.5=7.536(t)
(3)沙堆重:
答:这堆沙子大约重7.536吨。
(4÷2)2×3.14=12.56(m2)
×12.56×1.2 = 5.024(m3)
一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V圆锥= Sh
=
×19 ×12=76(cm )
答:这个零件的体积是76cm 。
2.如右图,一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高是6cm。每立方厘米钢大约重7.9g。这个铅锤大约重多少克 (得数保留整数。)
(2)铅锤的体积:
(1)铅锤的底面积:
25.12×7.9=198.448 ≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198克 。
×12.56×6=25.12(cm3)
(4÷2)2×3.14=12.56 (cm2)
3.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
= ×3.14×(31.4÷3.14÷2)2×9
= 235.5(cm3)
1
3
V = π( )2h
2π
C
答:它的体积是235.5cm3。
4.把一个圆锥沿着高切开,得到两个如图所示的图形,表面积增加了24 cm2。圆锥的高是6 cm,那么圆锥的体积是多少立方厘米?
5.有一个圆锥形沙堆,底面周长是9.42 m,高是1.5 m。如果将这些沙子铺在一个长6 m,宽2 m的长方体沙坑里,大约能铺多少厘米厚?(得数保留整数)
6.一个底面直径是16 cm的圆柱形容器中装有一些水,把一个底面半径是5 cm的圆锥形铁块完全浸没在水中,水未溢出,容器内的水上升了2.5 cm,圆锥形铁块的高是多少厘米?
3.14×(16÷2)2×2.5×3÷(3.14×52)=19.2(cm)
答:圆锥形铁块的高是19.2 cm。
这节课
你有什么收获?
2. 圆锥的体积公式用字母表示为V= Sh或
V= πr h。
3. 当已知圆锥的底面周长和高,可利用公式
来计算圆锥的体积。
1. 圆锥的体积等于与它等底等高的圆柱体积的 。
