抛物线的几何性质
图片预览





文档简介
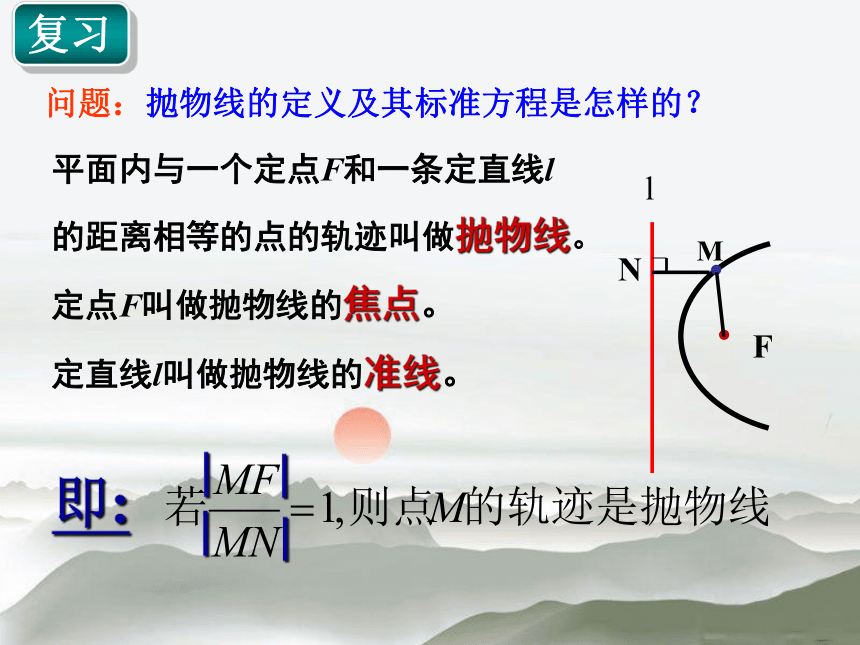
课件26张PPT。抛物线的几何性质平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l叫做抛物线的准线。 问题:抛物线的定义及其标准方程是怎样的? 复习 练习:填空(顶点在原点,焦点在坐标轴上) 开口向右开口向左开口向上开口向下以抛物线的标准方程:
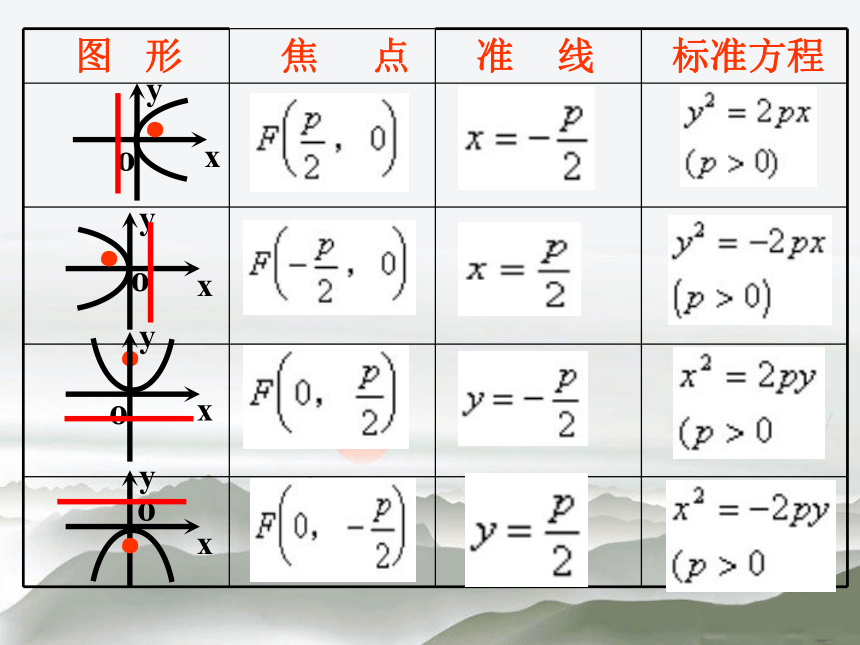
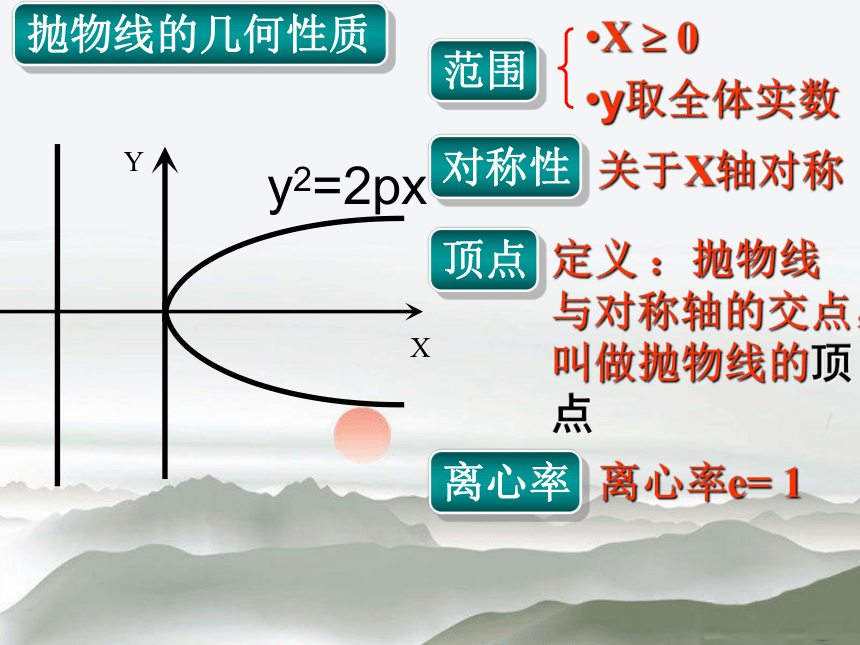
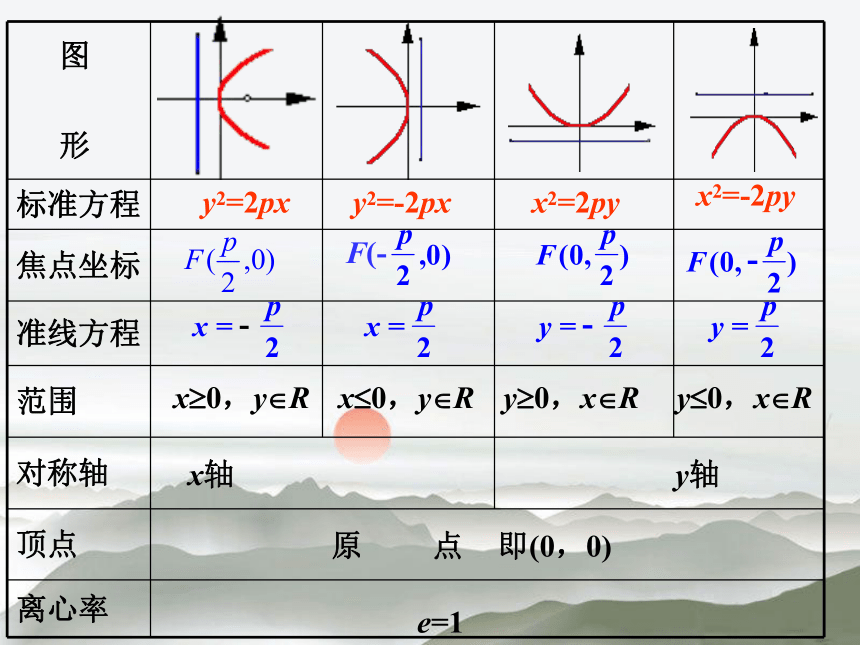
来研究它的几何性质. (图形 对称轴 顶点 离心率 准线 焦点 ) 抛物线的几何性质y2=2pxy取全体实数X ? 0范围对称性关于X轴对称顶点定义 :抛物线与对称轴的交点,叫做抛物线的顶点离心率离心率e= 1抛物线的几何性质y2=2pxy2=-2pxx2=2pyx2=-2pyF(----x?0,y?Rx?0,y?R y?0,x?Ry?0,x?R原 点即(0,0)e=1x轴y轴问题:与椭圆、双曲线的几何性质比较,抛物线的几何性质
有什么特点? (1)抛物线只位于半个坐标平面内,虽然它也可以无限延伸,
但没有渐近线; 2)抛物线只有一条对称轴,没有对称中心;3)抛物线只有一个顶点、一个焦点、一条准线;4)抛物线只有一个顶点、一个焦点、一条准线;抛物线由P决定开口大小 , P越大开口越大 而椭圆、双曲线由e决定 抛物线的顶点在原点,对称轴重合于椭
圆 短轴所在的直线,抛物线焦点
到顶点的距离为3,求抛物线的方程及抛物线
的准线方程。例1:求抛物线的标准方程及几何性质练习求符合下列条件的抛物线的标准方程(1)顶点在原点,关于x轴对称,并且经过点
M(5,-4);
(2)顶点在原点,焦点是F(0,5);
(3)顶点在原点,准线是x=4;
(4)焦点是F(0,-8),准线是y=8。2.一条隧道的顶部是抛物拱形,拱高是1.1m,跨度是2.2m。求拱形的抛物线方程。练习例2 斜率为1的直线L经过抛物线y2=4x的焦点,且与抛物线相交于A、B两点,求线段AB的长.法3 |AB|=x1+x2+P法1 利用两点间距离公式 法2 练习B练习例3:探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深40cm,求抛物线的标准方程及焦点的位置。FyxO解:如图所示,在探照灯的轴截面所在平面建立直角坐标系,使反光镜的顶点与原点重合,x轴垂直于灯口直径。AB 设抛物线的标准方程是:
由已知条件可得点A的坐标是(40,30),代入方程可得
所求的标准方程为
焦点坐标为
分析:观察图,正三角形及抛物线都是轴 对称图形,如果能证明x轴是它们的公共的对称轴,则容易求出三角形的边长. 1、已知抛物线的顶点在原点,对称
轴为x轴,焦点在直线3x-4y-12=0上,那
么抛物线通径长是 .
2、一个正三角形的三个顶点,都在抛
物线 上,其中一个顶点为坐标
原点,则这个三角形的面积为 。课堂练习3:葡萄美酒夜光杯,
欲饮琵琶马上催.问题1:如果测量得酒杯杯口宽4cm,杯深8cm,试求出该抛物线方程?4cm8cm解:如图建立平面直角坐标系,
则可知A(-2,8),B(2,8)
所以设抛物线的方程
为:
A、B点在抛物线上,代入抛
物线方程,可得P= ,
则所求的抛物线方程为:y轴(0,0)e=1问题2:研究酒杯轴截面所在曲线的几何性质。 例1 已知抛物线关于 轴对称,它的顶点在坐标原点,并且经过点 ,求它的标准方程,A
B思考2:三角形OAB为等边三角形,若AB垂直于X轴,求AB的长度思考3:当等腰直角三角形OAB中OA垂直于OB呢,三角形面积?思考1:当CD过焦点,线CD的长为多少?C
DF
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l叫做抛物线的准线。 问题:抛物线的定义及其标准方程是怎样的? 复习 练习:填空(顶点在原点,焦点在坐标轴上) 开口向右开口向左开口向上开口向下以抛物线的标准方程:
来研究它的几何性质. (图形 对称轴 顶点 离心率 准线 焦点 ) 抛物线的几何性质y2=2pxy取全体实数X ? 0范围对称性关于X轴对称顶点定义 :抛物线与对称轴的交点,叫做抛物线的顶点离心率离心率e= 1抛物线的几何性质y2=2pxy2=-2pxx2=2pyx2=-2pyF(----x?0,y?Rx?0,y?R y?0,x?Ry?0,x?R原 点即(0,0)e=1x轴y轴问题:与椭圆、双曲线的几何性质比较,抛物线的几何性质
有什么特点? (1)抛物线只位于半个坐标平面内,虽然它也可以无限延伸,
但没有渐近线; 2)抛物线只有一条对称轴,没有对称中心;3)抛物线只有一个顶点、一个焦点、一条准线;4)抛物线只有一个顶点、一个焦点、一条准线;抛物线由P决定开口大小 , P越大开口越大 而椭圆、双曲线由e决定 抛物线的顶点在原点,对称轴重合于椭
圆 短轴所在的直线,抛物线焦点
到顶点的距离为3,求抛物线的方程及抛物线
的准线方程。例1:求抛物线的标准方程及几何性质练习求符合下列条件的抛物线的标准方程(1)顶点在原点,关于x轴对称,并且经过点
M(5,-4);
(2)顶点在原点,焦点是F(0,5);
(3)顶点在原点,准线是x=4;
(4)焦点是F(0,-8),准线是y=8。2.一条隧道的顶部是抛物拱形,拱高是1.1m,跨度是2.2m。求拱形的抛物线方程。练习例2 斜率为1的直线L经过抛物线y2=4x的焦点,且与抛物线相交于A、B两点,求线段AB的长.法3 |AB|=x1+x2+P法1 利用两点间距离公式 法2 练习B练习例3:探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深40cm,求抛物线的标准方程及焦点的位置。FyxO解:如图所示,在探照灯的轴截面所在平面建立直角坐标系,使反光镜的顶点与原点重合,x轴垂直于灯口直径。AB 设抛物线的标准方程是:
由已知条件可得点A的坐标是(40,30),代入方程可得
所求的标准方程为
焦点坐标为
分析:观察图,正三角形及抛物线都是轴 对称图形,如果能证明x轴是它们的公共的对称轴,则容易求出三角形的边长. 1、已知抛物线的顶点在原点,对称
轴为x轴,焦点在直线3x-4y-12=0上,那
么抛物线通径长是 .
2、一个正三角形的三个顶点,都在抛
物线 上,其中一个顶点为坐标
原点,则这个三角形的面积为 。课堂练习3:葡萄美酒夜光杯,
欲饮琵琶马上催.问题1:如果测量得酒杯杯口宽4cm,杯深8cm,试求出该抛物线方程?4cm8cm解:如图建立平面直角坐标系,
则可知A(-2,8),B(2,8)
所以设抛物线的方程
为:
A、B点在抛物线上,代入抛
物线方程,可得P= ,
则所求的抛物线方程为:y轴(0,0)e=1问题2:研究酒杯轴截面所在曲线的几何性质。 例1 已知抛物线关于 轴对称,它的顶点在坐标原点,并且经过点 ,求它的标准方程,A
B思考2:三角形OAB为等边三角形,若AB垂直于X轴,求AB的长度思考3:当等腰直角三角形OAB中OA垂直于OB呢,三角形面积?思考1:当CD过焦点,线CD的长为多少?C
DF
