直线与抛物线的位置关系
图片预览



文档简介
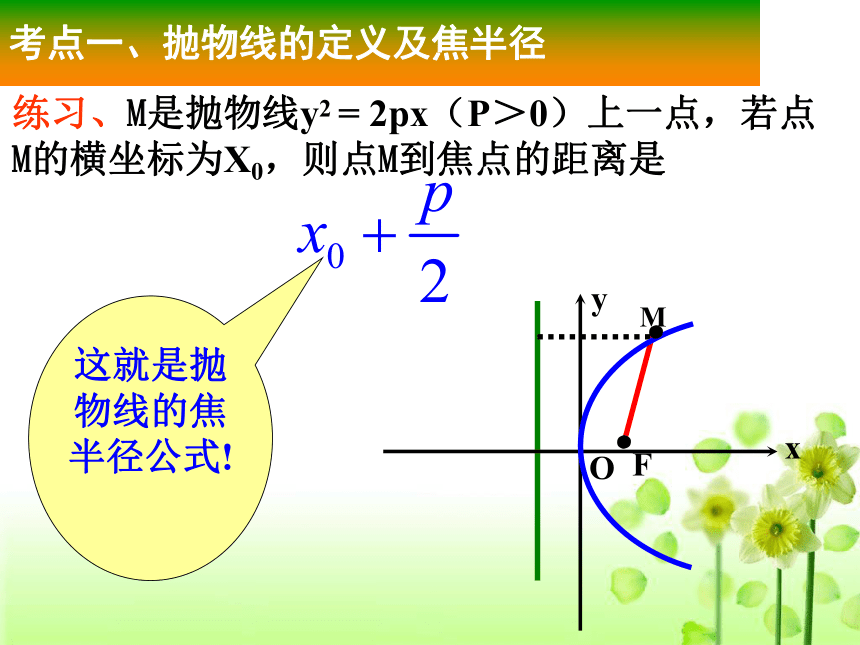
课件13张PPT。直线与抛物线的位置关系练习、M是抛物线y2 = 2px(P>0)上一点,若点
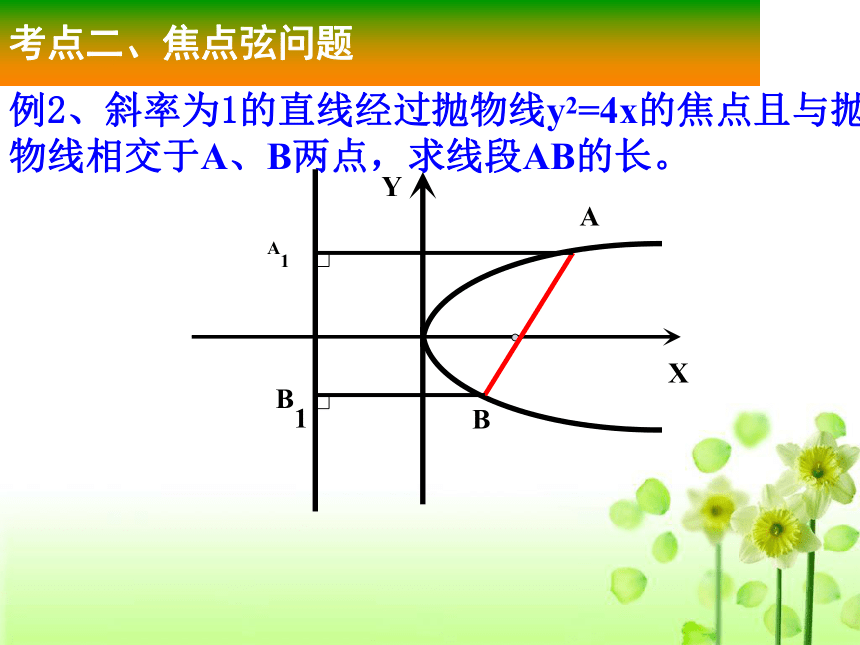
M的横坐标为X0,则点M到焦点的距离是 这就是抛物线的焦半径公式!考点一、抛物线的定义及焦半径例2、斜率为1的直线经过抛物线y2=4x的焦点且与抛物线相交于A、B两点,求线段AB的长。考点二、焦点弦问题运用2、过抛物线 的焦点,作倾斜角为的直线,则被抛物线截得的弦长为?运用1、过抛物线y2=4x的焦点作直线交于A(x1,y1),
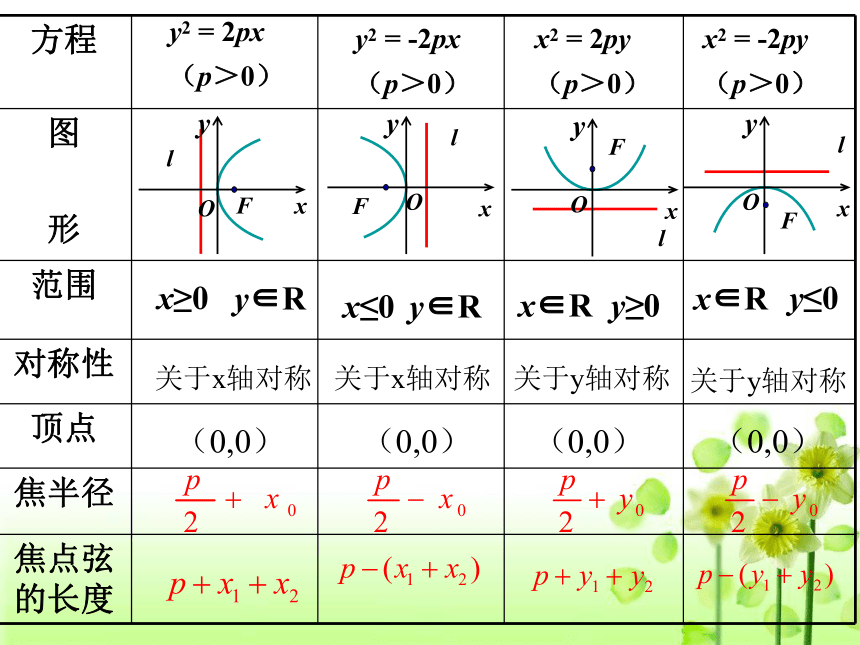
B(x2,y2)两点,如果x1+x2=6,求|AB|的值y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)练习、已知抛物线的顶点在原点,对称轴为x轴,
焦点在直线3x-4y-12=0上,求抛物线通径长.通径:经过抛物线的焦点并且垂直于抛物线的轴所得的弦叫作抛物线的通径,长为2p.1、相离;2、相切;
3、相交(一个交点,两个交点)考点三、直线与抛物线位置关系1、直线与抛物线的对称轴平行例:计算直线y = 6与抛物线y2 =4x的位置关系计算结果:得到一元一次方程,容易解出交点坐标2、直线与抛物线的对称轴不平行计算直线 y = x -1与抛
物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相交。例3、已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线:
(1)两个公共点;
(2)没有公共点。
(3)只有一个公共点;考点四、与弦长、中点有关的问题考点五、最值问题例7、在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离。yxL·P练习、在抛物线y2=2x上求一点P,使P到直线
x-y+3=0的距离最短,并求出距离的最小值.
M的横坐标为X0,则点M到焦点的距离是 这就是抛物线的焦半径公式!考点一、抛物线的定义及焦半径例2、斜率为1的直线经过抛物线y2=4x的焦点且与抛物线相交于A、B两点,求线段AB的长。考点二、焦点弦问题运用2、过抛物线 的焦点,作倾斜角为的直线,则被抛物线截得的弦长为?运用1、过抛物线y2=4x的焦点作直线交于A(x1,y1),
B(x2,y2)两点,如果x1+x2=6,求|AB|的值y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)练习、已知抛物线的顶点在原点,对称轴为x轴,
焦点在直线3x-4y-12=0上,求抛物线通径长.通径:经过抛物线的焦点并且垂直于抛物线的轴所得的弦叫作抛物线的通径,长为2p.1、相离;2、相切;
3、相交(一个交点,两个交点)考点三、直线与抛物线位置关系1、直线与抛物线的对称轴平行例:计算直线y = 6与抛物线y2 =4x的位置关系计算结果:得到一元一次方程,容易解出交点坐标2、直线与抛物线的对称轴不平行计算直线 y = x -1与抛
物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相交。例3、已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线:
(1)两个公共点;
(2)没有公共点。
(3)只有一个公共点;考点四、与弦长、中点有关的问题考点五、最值问题例7、在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离。yxL·P练习、在抛物线y2=2x上求一点P,使P到直线
x-y+3=0的距离最短,并求出距离的最小值.
