双曲线的简单几何性质
图片预览







文档简介
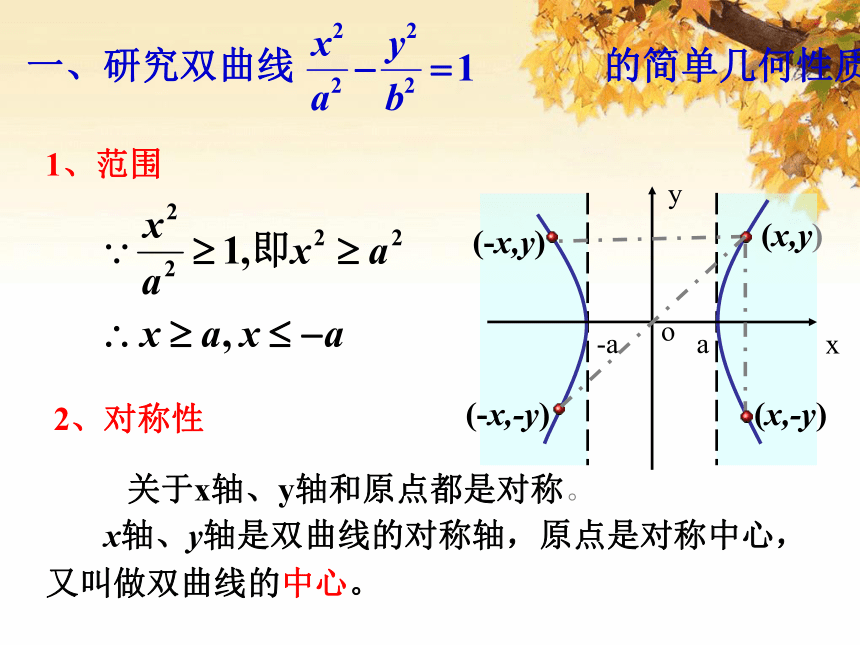
课件22张PPT。双曲线的简单几何性质| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c) 2、对称性一、研究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称。 x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.(2)4、渐近线(3)利用渐近线可以较准确的
画出双曲线的草图.双曲线的渐近线方程
对于双曲线 ,把方程右
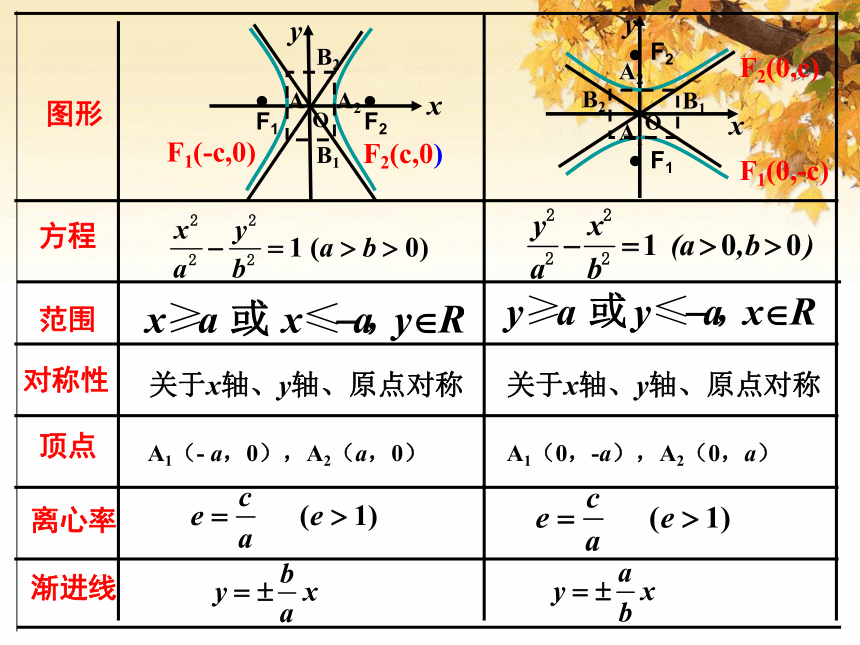
边的“1”换成“0”,得双曲线渐近线方程.思考:对于双曲线 的渐近线有怎样的结论呢?5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:(4)等轴双曲线的离心率e= ?( 5 )(1)范围:(4)渐近线:(5)离心率:关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)A1(0,-a),A2(0,a)关于x轴、y轴、原点对称渐进线F2(0,c)
F1(0,-c)解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3焦点坐标是(0,-5),(0,5)渐近线方程:练习:P53 T1半焦距离心率:例2思考:一个双曲线的渐近线的方程为: ,它的离心率为 .练习:求出下列双曲线的标准方程DA关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)A1(0,-a),A2(0,a)关于x轴、y轴、原点对称渐进线F2(0,c)
F1(0,-c) 双曲线的渐近线方程为 解出 .练习:
已知双曲线的两条渐进线方程是
焦点坐标是
求此双曲线的方程 练习
(1) :(2) : 的渐近线方程为: 的实轴长 虚轴长为_____ 顶点坐标为 ,焦点坐标为_________
离心率为_______4的渐近线方程为: 的渐近线方程为: 的渐近线方程为:
画出双曲线的草图.双曲线的渐近线方程
对于双曲线 ,把方程右
边的“1”换成“0”,得双曲线渐近线方程.思考:对于双曲线 的渐近线有怎样的结论呢?5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:(4)等轴双曲线的离心率e= ?( 5 )(1)范围:(4)渐近线:(5)离心率:关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)A1(0,-a),A2(0,a)关于x轴、y轴、原点对称渐进线F2(0,c)
F1(0,-c)解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3焦点坐标是(0,-5),(0,5)渐近线方程:练习:P53 T1半焦距离心率:例2思考:一个双曲线的渐近线的方程为: ,它的离心率为 .练习:求出下列双曲线的标准方程DA关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)A1(0,-a),A2(0,a)关于x轴、y轴、原点对称渐进线F2(0,c)
F1(0,-c) 双曲线的渐近线方程为 解出 .练习:
已知双曲线的两条渐进线方程是
焦点坐标是
求此双曲线的方程 练习
(1) :(2) : 的渐近线方程为: 的实轴长 虚轴长为_____ 顶点坐标为 ,焦点坐标为_________
离心率为_______4的渐近线方程为: 的渐近线方程为: 的渐近线方程为:
