变化率与导数(第一课时)
图片预览







文档简介
课件23张PPT。人民教育出版社 高中数学 选修1-13.1 变化率与导数
(第一课时)教学过程一 引入谁是导数概念的第一发明人?二 传授新课学习活动:每人配备一个气球,以学习
小组的形式,吹气球,观察,
并思考:吹气球:每次都吹入差不多大小的一口气观察:气球变大的速度思考:每次吹入差不多大小的气体
气球变大的速度一样吗?
为什么?对思考的问题给一个科学的回答,就需要把这个生活现象从数学的角度,用数学语言进行描述,解决问题对一种生活现象的数学解释当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为这一现象中,哪些量在改变?
变量的变化情况?
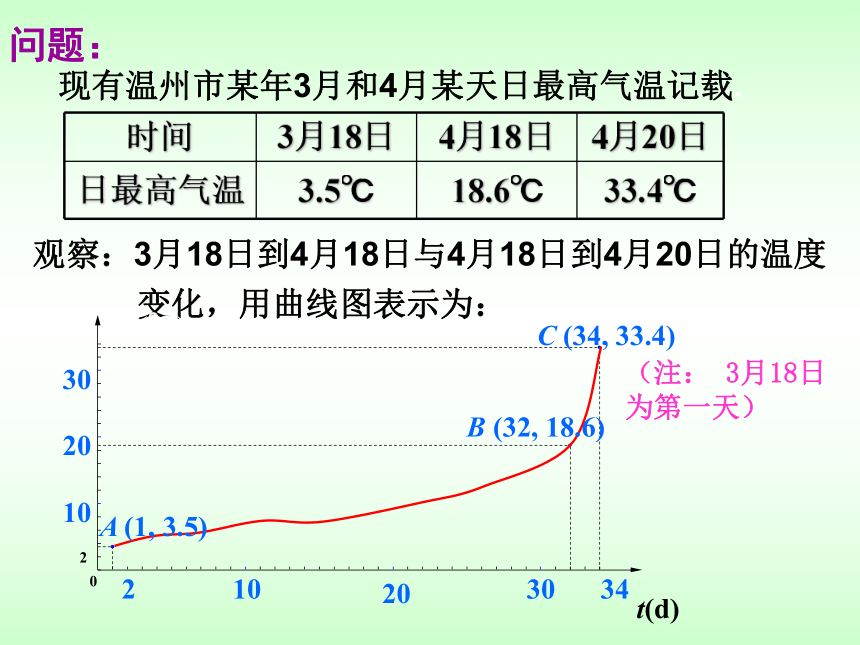
引入气球平均膨胀率的概念当空气容量V从1L增加到2 L , 气球半径增加了气球的平均膨胀率为当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为 随着气球体积逐渐变大,它的平均膨胀率逐渐变小当空气容量V从1L增加到2 L , 气球半径增加了气球的平均膨胀率为当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?现有温州市某年3月和4月某天日最高气温记载.观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:(注: 3月18日为第一天)问题:问题1:“气温陡增”是一句生活用语,它的数学意义
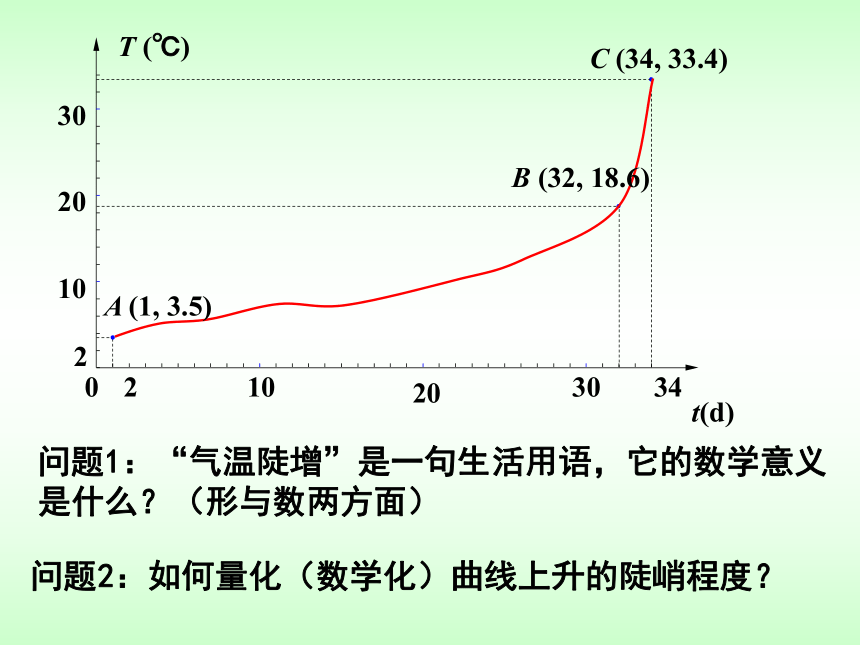
是什么?(形与数两方面)问题2:如何量化(数学化)曲线上升的陡峭程度?(1 )曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度。(2)由点B上升到C点,必须考察yC—yB的大小,但仅仅注意
yC—yB的大小能否精确量化BC段陡峭程度,为什么?在考察yC—yB的同时必须考察xC—xB,函数的本质在于一个
量的改变本身就隐含着这种改变必定相对于另一个量的改变。(3)我们用比值 近似地量化B、C这一段曲线的陡峭程度,并称该比值为【32,34】上的平均变化率(4)分别计算气温在区间【1,32】 【32,34】的平均变化率现在回答问题1:“气温陡增”是一句生活用语,它的
数学意义是什么?(形与数两方面)探究活动 “气球的平均膨胀率”是一个特殊的情况,
“气温陡增”也是一个特殊的情况,
我们把这一思路延伸到函数上:函数的平均变化率定义:平均变化率: 式子 称为函数 f (x)从x1到 x2的平均变化率.令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则探究活动 思考:平均变化率的几何意义?
flash动画演示两点间的斜率.例:荣勃去崩极,假设荣勃下降的运动符合方程 , 请同学们计算荣勃从3秒到4秒间的平均速度,计算从9秒到10秒的平均速度。 实践活动探究活动 观看十运会中跳水男子十米台田亮逆转夺冠的影片剪辑请同学们把这一生活现象用数学语言来解释。你能描绘出田亮重心移动的图像吗? 实践活动 假设相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.,那么田亮在0秒到0.5秒时间段内的平均速度是多少,在1秒到2秒时间段内呢,在 时间段内呢? 小结 (1)变化率的概念(2)注意发现生活中和变化率有关的例子 课外思考 思考:关于田亮跳水的例子,当我们计算田亮在某一段时间里的平均变化率分别为正数,负数,0的时候,其运动状态是怎样的?能不能用平均变化率精确的表示田亮的运动状态呢? 理解:
1,式子中△x 、△ y 的值可正、可负,但
的△x值不能为0, △ y 的值可以为0
2,若函数f (x)为常函数时, △ y =0
3, 变式练习: 1.甲用5年时间挣到10万元, 乙用5个月时间挣到2万元, 如何比较和评价甲、乙两人的经营成果? 2.已知函数 f (x) = 2 x +1, g (x) = – 2 x, 分别计算在下列区间上 f (x) 及 g (x) 的平均变化率.(1) [ –3 , –1] ; (2) [ 0 , 5 ] .做两个题吧!1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=( )
A 、 3 B、 3Δx-(Δx)2
C 、 3-(Δx)2 D 、3-Δx D2、求y=x2在x=x0附近的平均变化率.
2x0+Δx 小结:1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
(第一课时)教学过程一 引入谁是导数概念的第一发明人?二 传授新课学习活动:每人配备一个气球,以学习
小组的形式,吹气球,观察,
并思考:吹气球:每次都吹入差不多大小的一口气观察:气球变大的速度思考:每次吹入差不多大小的气体
气球变大的速度一样吗?
为什么?对思考的问题给一个科学的回答,就需要把这个生活现象从数学的角度,用数学语言进行描述,解决问题对一种生活现象的数学解释当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为这一现象中,哪些量在改变?
变量的变化情况?
引入气球平均膨胀率的概念当空气容量V从1L增加到2 L , 气球半径增加了气球的平均膨胀率为当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为 随着气球体积逐渐变大,它的平均膨胀率逐渐变小当空气容量V从1L增加到2 L , 气球半径增加了气球的平均膨胀率为当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球的平均膨胀率为 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?现有温州市某年3月和4月某天日最高气温记载.观察:3月18日到4月18日与4月18日到4月20日的温度变化,用曲线图表示为:(注: 3月18日为第一天)问题:问题1:“气温陡增”是一句生活用语,它的数学意义
是什么?(形与数两方面)问题2:如何量化(数学化)曲线上升的陡峭程度?(1 )曲线上BC之间一段几乎成了“直线”,由此联想如何量化直线的倾斜程度。(2)由点B上升到C点,必须考察yC—yB的大小,但仅仅注意
yC—yB的大小能否精确量化BC段陡峭程度,为什么?在考察yC—yB的同时必须考察xC—xB,函数的本质在于一个
量的改变本身就隐含着这种改变必定相对于另一个量的改变。(3)我们用比值 近似地量化B、C这一段曲线的陡峭程度,并称该比值为【32,34】上的平均变化率(4)分别计算气温在区间【1,32】 【32,34】的平均变化率现在回答问题1:“气温陡增”是一句生活用语,它的
数学意义是什么?(形与数两方面)探究活动 “气球的平均膨胀率”是一个特殊的情况,
“气温陡增”也是一个特殊的情况,
我们把这一思路延伸到函数上:函数的平均变化率定义:平均变化率: 式子 称为函数 f (x)从x1到 x2的平均变化率.令△x = x2 – x1 , △ y = f (x2) – f (x1) ,则探究活动 思考:平均变化率的几何意义?
flash动画演示两点间的斜率.例:荣勃去崩极,假设荣勃下降的运动符合方程 , 请同学们计算荣勃从3秒到4秒间的平均速度,计算从9秒到10秒的平均速度。 实践活动探究活动 观看十运会中跳水男子十米台田亮逆转夺冠的影片剪辑请同学们把这一生活现象用数学语言来解释。你能描绘出田亮重心移动的图像吗? 实践活动 假设相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10.,那么田亮在0秒到0.5秒时间段内的平均速度是多少,在1秒到2秒时间段内呢,在 时间段内呢? 小结 (1)变化率的概念(2)注意发现生活中和变化率有关的例子 课外思考 思考:关于田亮跳水的例子,当我们计算田亮在某一段时间里的平均变化率分别为正数,负数,0的时候,其运动状态是怎样的?能不能用平均变化率精确的表示田亮的运动状态呢? 理解:
1,式子中△x 、△ y 的值可正、可负,但
的△x值不能为0, △ y 的值可以为0
2,若函数f (x)为常函数时, △ y =0
3, 变式练习: 1.甲用5年时间挣到10万元, 乙用5个月时间挣到2万元, 如何比较和评价甲、乙两人的经营成果? 2.已知函数 f (x) = 2 x +1, g (x) = – 2 x, 分别计算在下列区间上 f (x) 及 g (x) 的平均变化率.(1) [ –3 , –1] ; (2) [ 0 , 5 ] .做两个题吧!1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=( )
A 、 3 B、 3Δx-(Δx)2
C 、 3-(Δx)2 D 、3-Δx D2、求y=x2在x=x0附近的平均变化率.
2x0+Δx 小结:1.函数的平均变化率2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
