导数的几何意义(一)(上课)
图片预览





文档简介
课件22张PPT。导数的几何意义
复习1、平均变化率?2、平均变化率的几何意义?3、瞬时变化率?4、瞬时变化率的几何意义? 概括:函数 在 处的
导数 的几何意义就是函数
的图像在点
处的切线AD的斜率.
(数形结合)
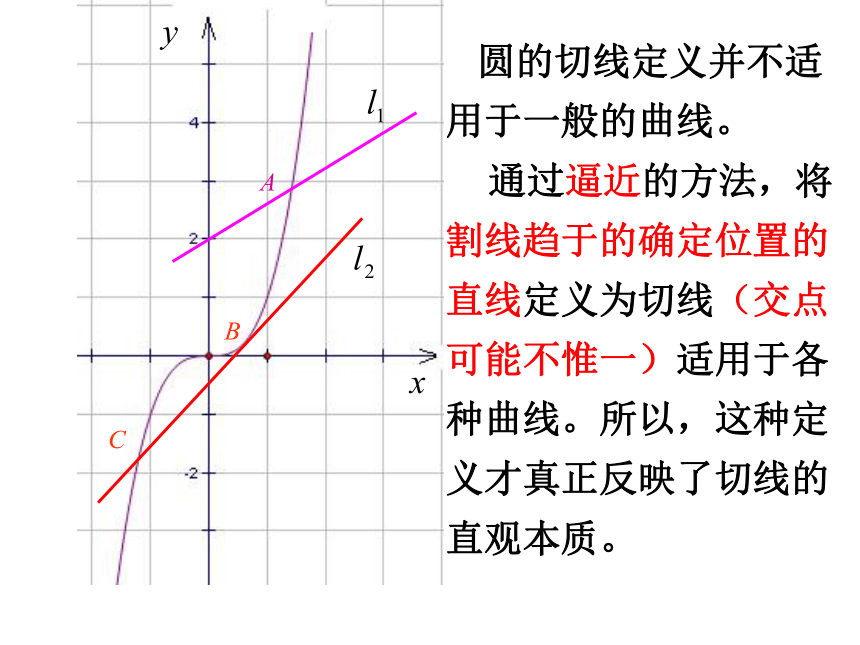
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
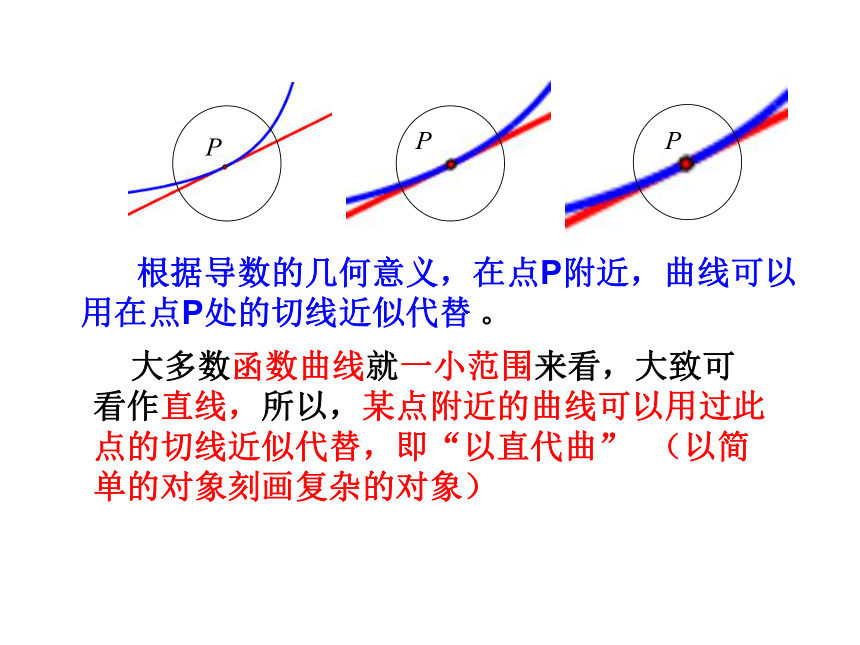
练习:求y=x3在(0,0)处的切线方程 根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)
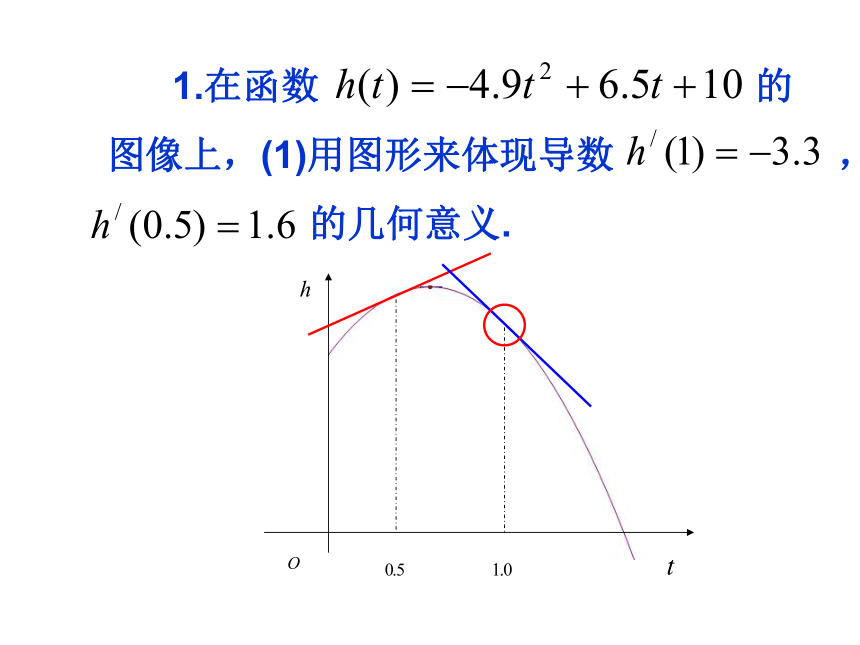
1.在函数 的
图像上,(1)用图形来体现导数 ,
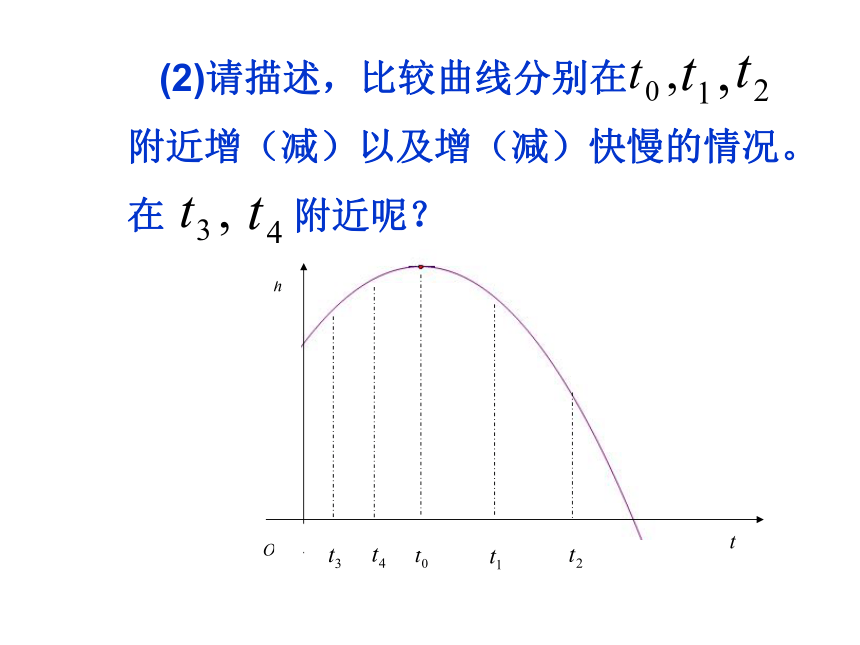
的几何意义. (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? 增(减):增(减)快慢:=切线的斜率附近:瞬时变化率(正或负)即:瞬时变化率(导数)(数形结合,以直代曲)画切线即:导数的绝多值的大小=切线斜率的绝对值的
大小切线的倾斜程度
(陡峭程度)以简单对象刻画复杂的对象(2) 曲线在 时,切线平行于x轴,曲线在
附近比较平坦,几乎没有升降. 曲线在 处切线 的斜率 0
在 附近,曲线 ,函数在
附近单调 如图,切线 的倾斜程度大于切线 的
倾斜程度, 大于上升递增上升 这说明曲线在 附近比在 附近
得迅速. 递减下降小于下降
2.如图表示人体血管中的药物浓度c=f(t)
(单位:mg/ml)随时间t(单位:min)
变化的函数图像,根据图像,估计
t=0.2,0.4,0.6,0.8(min)时,血管中
药物浓度的瞬时变化率,把数据用表格
的形式列出。(精确到0.1)
血管中药物浓度的瞬时变化率,就是药物浓度从图象上看,它表示曲线在该点处的切线的斜率.函数f(t)在此时刻的导数,(数形结合,以直代曲)以简单对象刻画复杂的对象
抽象概括:
是确定的数是 的函数 导函数 的概念:因此,切线方程为y-2=2(x-1),
即y=2x.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即归纳:求切线方程的步骤 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念。
练习:小结:
1.函数 在 处的导数
的几何意义,就是函数 的图像在点
处的切线AD的斜率(数形结合)
=切线 AD的斜率3.导函数(简称导数) 2.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学
思想方法。 以简单对象刻画复杂的对象谢谢
复习1、平均变化率?2、平均变化率的几何意义?3、瞬时变化率?4、瞬时变化率的几何意义? 概括:函数 在 处的
导数 的几何意义就是函数
的图像在点
处的切线AD的斜率.
(数形结合)
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
练习:求y=x3在(0,0)处的切线方程 根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)
1.在函数 的
图像上,(1)用图形来体现导数 ,
的几何意义. (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? 增(减):增(减)快慢:=切线的斜率附近:瞬时变化率(正或负)即:瞬时变化率(导数)(数形结合,以直代曲)画切线即:导数的绝多值的大小=切线斜率的绝对值的
大小切线的倾斜程度
(陡峭程度)以简单对象刻画复杂的对象(2) 曲线在 时,切线平行于x轴,曲线在
附近比较平坦,几乎没有升降. 曲线在 处切线 的斜率 0
在 附近,曲线 ,函数在
附近单调 如图,切线 的倾斜程度大于切线 的
倾斜程度, 大于上升递增上升 这说明曲线在 附近比在 附近
得迅速. 递减下降小于下降
2.如图表示人体血管中的药物浓度c=f(t)
(单位:mg/ml)随时间t(单位:min)
变化的函数图像,根据图像,估计
t=0.2,0.4,0.6,0.8(min)时,血管中
药物浓度的瞬时变化率,把数据用表格
的形式列出。(精确到0.1)
血管中药物浓度的瞬时变化率,就是药物浓度从图象上看,它表示曲线在该点处的切线的斜率.函数f(t)在此时刻的导数,(数形结合,以直代曲)以简单对象刻画复杂的对象
抽象概括:
是确定的数是 的函数 导函数 的概念:因此,切线方程为y-2=2(x-1),
即y=2x.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即归纳:求切线方程的步骤 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念。
练习:小结:
1.函数 在 处的导数
的几何意义,就是函数 的图像在点
处的切线AD的斜率(数形结合)
=切线 AD的斜率3.导函数(简称导数) 2.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学
思想方法。 以简单对象刻画复杂的对象谢谢
