3.2导数的计算
图片预览








文档简介
课件22张PPT。几种常见函数的导数一、复习1.解析几何中,过曲线某点的切线的斜率的精确描述与
求值;物理学中,物体运动过程中,在某时刻的瞬时速
度的精确描述与求值等,都是极限思想得到本质相同
的数学表达式,将它们抽象归纳为一个统一的概念和
公式——导数,导数源于实践,又服务于实践.2.求函数的导数的方法是:说明:上面的方法中把x换x0即为求函数在点x0处的
导数. 3.函数f(x)在点x0处的导数 就是导函数 在x=
x0处的函数值,即 .这也是求函数在点x0
处的导数的方法之一。 4.函数 y=f(x)在点x0处的导数的几何意义,就是曲线y=
f(x)在点P(x0 ,f(x0))处的切线的斜率.5.求切线方程的步骤:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即二、新课——几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式1: .公式2: .公式3: .公式4: 三、例题选讲例1:求过曲线y=cosx上点P( )且与过这点的切线垂
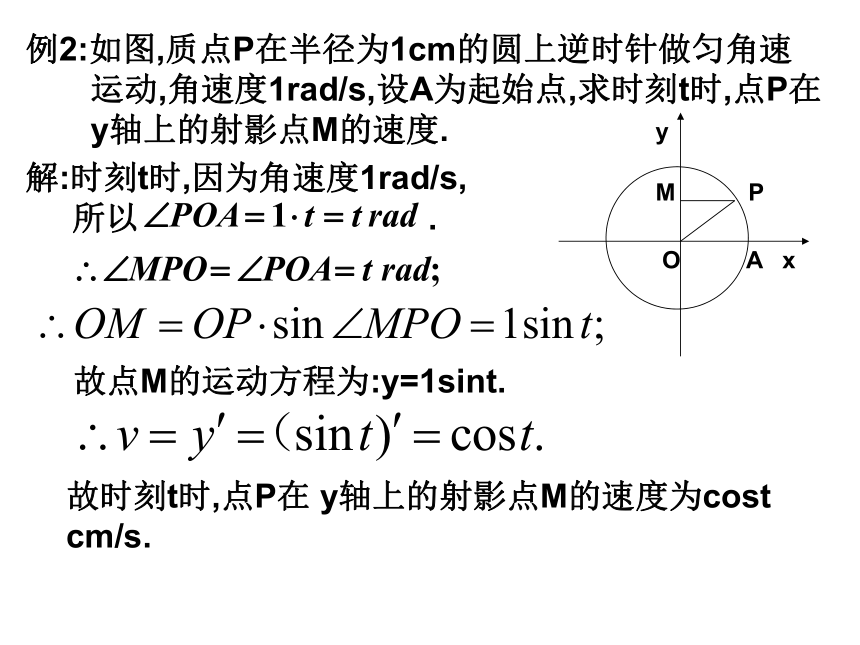
直的直线方程.注:满足条件的直线称为曲线在P点的法线.O A xM Py例2:如图,质点P在半径为1cm的圆上逆时针做匀角速
运动,角速度1rad/s,设A为起始点,求时刻t时,点P在
y轴上的射影点M的速度.解:时刻t时,因为角速度1rad/s,
所以 .故点M的运动方程为:y=1sint.故时刻t时,点P在 y轴上的射影点M的速度为cost
cm/s.例3:已知两条曲线y=sinx,y=cosx,问是否存在这两条
曲线的一个公共点,使在这一点处,两条曲线的切线
互相垂直?并说明理由.解:设存在一个公共点P(x0,y0)满足题设条件.由两条曲线的切线在点P互相垂直,则cosx0(-sinx0)
=-1,得sinx0cosx0=1,即sin2x0=2.这不可能,所以不存在满足题设条件的一个点.练习1:曲线y=sinx在点P( )处的切线的斜率为
___________.例4:已知曲线 在点P(1,1)处的切线与直线m平行且
距离等于 ,求直线m的方程.设直线m的方程为3x+y+b=0,由平行线间的距离公式得:故所求的直线m的方程为3x+y+6=0或3x+y-14=0.导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:例4:求下列函数的导数:答案:四、小结与作业1.要切实掌握四种常见函数的导数公式:(1) (c为常
数;(2) ;(3) ;(4)2.对于简单函数的求导,关键是合理转化函数关系式为
可以直接应用公式的基本函数的模式.3.能结合直线的知识来解决一些与切线有关的较为综
合性问题.我们今后可以直接使用的基本初等函数的导数公式我们今后可以直接使用的基本初等函数的导数公式例2.求函数y=x3-2x+3的导数.练习: P92 1、2
例4:求下列函数的导数:答案:例5.某运动物体自始点起经过t秒后的距离s满足s=
-4t3+16t2.
(1)此物体什么时刻在始点?
(2)什么时刻它的速度为零?解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得:
t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在
始点. 即t3-12t2+32t=0,
解得:t1=0,t2=4,t3=8,故在t=0,t=4和t=8秒时物体运动的速度为零.例6.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均
相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).对于 则与S1相切于P点的切线方程为y-x12
=2x1(x-x1),即y=2x1x-x12.①对于 与S2相切于Q点的切线方程为y+
(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4.②因为两切线重合,若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4. 作业:
作业: P93 2、3、4、5
求值;物理学中,物体运动过程中,在某时刻的瞬时速
度的精确描述与求值等,都是极限思想得到本质相同
的数学表达式,将它们抽象归纳为一个统一的概念和
公式——导数,导数源于实践,又服务于实践.2.求函数的导数的方法是:说明:上面的方法中把x换x0即为求函数在点x0处的
导数. 3.函数f(x)在点x0处的导数 就是导函数 在x=
x0处的函数值,即 .这也是求函数在点x0
处的导数的方法之一。 4.函数 y=f(x)在点x0处的导数的几何意义,就是曲线y=
f(x)在点P(x0 ,f(x0))处的切线的斜率.5.求切线方程的步骤:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即二、新课——几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式1: .公式2: .公式3: .公式4: 三、例题选讲例1:求过曲线y=cosx上点P( )且与过这点的切线垂
直的直线方程.注:满足条件的直线称为曲线在P点的法线.O A xM Py例2:如图,质点P在半径为1cm的圆上逆时针做匀角速
运动,角速度1rad/s,设A为起始点,求时刻t时,点P在
y轴上的射影点M的速度.解:时刻t时,因为角速度1rad/s,
所以 .故点M的运动方程为:y=1sint.故时刻t时,点P在 y轴上的射影点M的速度为cost
cm/s.例3:已知两条曲线y=sinx,y=cosx,问是否存在这两条
曲线的一个公共点,使在这一点处,两条曲线的切线
互相垂直?并说明理由.解:设存在一个公共点P(x0,y0)满足题设条件.由两条曲线的切线在点P互相垂直,则cosx0(-sinx0)
=-1,得sinx0cosx0=1,即sin2x0=2.这不可能,所以不存在满足题设条件的一个点.练习1:曲线y=sinx在点P( )处的切线的斜率为
___________.例4:已知曲线 在点P(1,1)处的切线与直线m平行且
距离等于 ,求直线m的方程.设直线m的方程为3x+y+b=0,由平行线间的距离公式得:故所求的直线m的方程为3x+y+6=0或3x+y-14=0.导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:例4:求下列函数的导数:答案:四、小结与作业1.要切实掌握四种常见函数的导数公式:(1) (c为常
数;(2) ;(3) ;(4)2.对于简单函数的求导,关键是合理转化函数关系式为
可以直接应用公式的基本函数的模式.3.能结合直线的知识来解决一些与切线有关的较为综
合性问题.我们今后可以直接使用的基本初等函数的导数公式我们今后可以直接使用的基本初等函数的导数公式例2.求函数y=x3-2x+3的导数.练习: P92 1、2
例4:求下列函数的导数:答案:例5.某运动物体自始点起经过t秒后的距离s满足s=
-4t3+16t2.
(1)此物体什么时刻在始点?
(2)什么时刻它的速度为零?解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得:
t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在
始点. 即t3-12t2+32t=0,
解得:t1=0,t2=4,t3=8,故在t=0,t=4和t=8秒时物体运动的速度为零.例6.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均
相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).对于 则与S1相切于P点的切线方程为y-x12
=2x1(x-x1),即y=2x1x-x12.①对于 与S2相切于Q点的切线方程为y+
(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4.②因为两切线重合,若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4. 作业:
作业: P93 2、3、4、5
