函数的单调性与导数
图片预览








文档简介
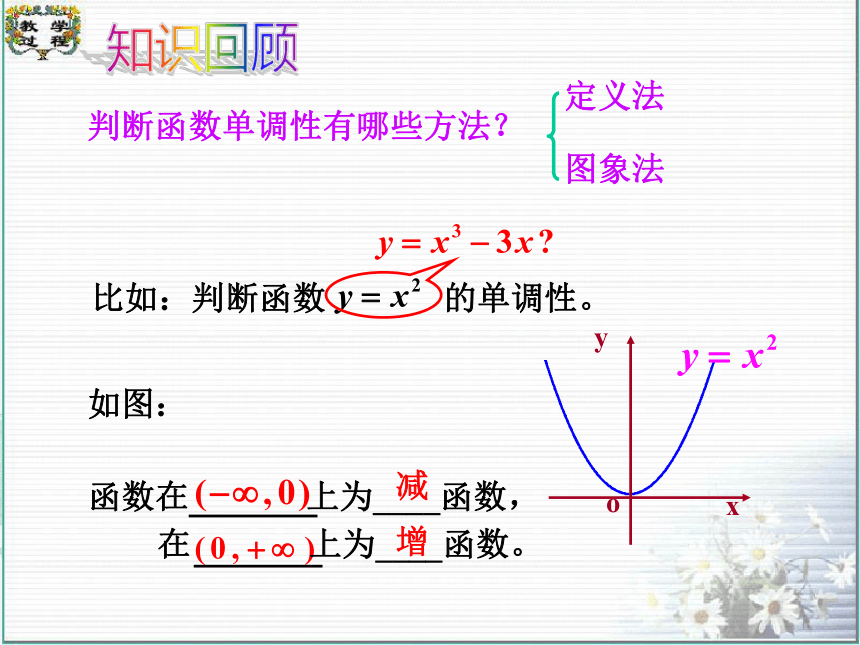
课件41张PPT。函数的单调性与导数知识回顾判断函数单调性有哪些方法?比如:判断函数 的单调性。图象法减增如图:动态
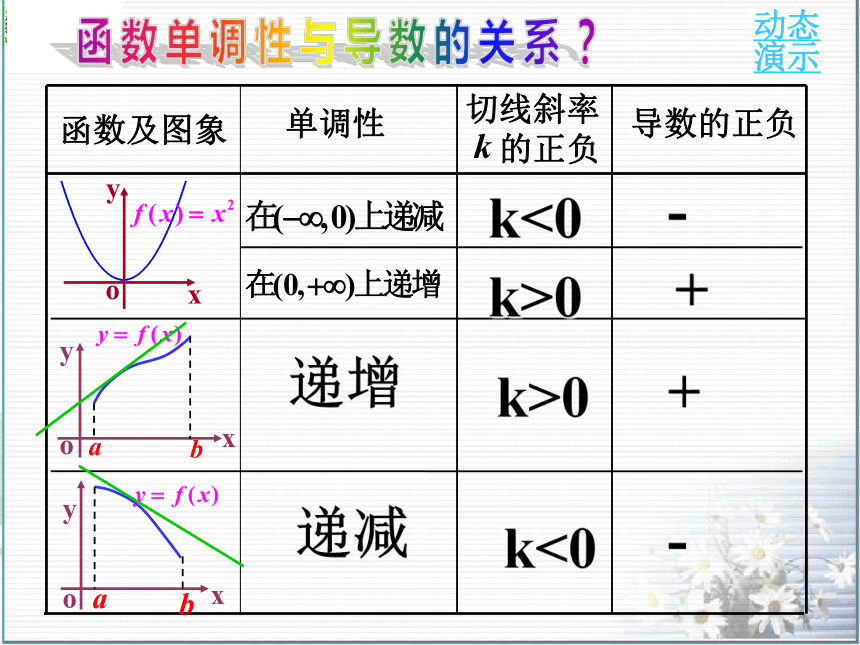
演示单调性导数的正负函数及图象切线斜率
的正负函数单调性与导数的关系?k>0k>0k<0k<0++--递增递减函数单调性与导数正负的关系注意:
应正确理解 “ 某个区间 ” 的含义, 它必是定义域内的某个区间。1.应用导数求函数的单调区间(选填:“增” ,“减” ,“既不是增函数,也不是减函数”)
(1) 函数y=x-3在[-3,5]上为__________函数。
(2) 函数 y = x2-3x 在[2,+∞)上为_____函数,
在(-∞,1]上为______函数,在[1,2]上为__
__________________________________函数。基础训练:应用举例增增减既不是增函数,也不是减函数求函数 的单调区间。变1:求函数 的单调区间。理解训练:解:的单调递增区间为单调递减区间为变3:求函数 的单调区间。解:解:总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳1°什么情况下,用“导数法” 求函数单调性、
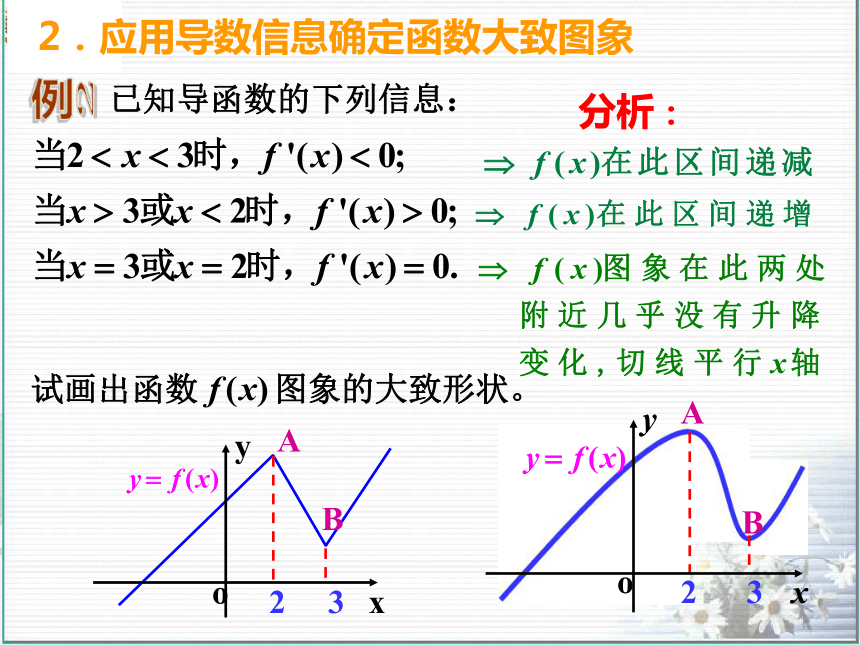
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归高考试(04年全国理)B尝已知导函数的下列信息:试画出函数 图象的大致形状。分析:2.应用导数信息确定函数大致图象已知导函数的下列信息:试画出函数 图象的大致形状。分析:2.应用导数信息确定函数大致图象解: 的大致形状如右图:(A)(B)(C)(D)C(04浙江理工类)高考试尝设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( ) 通过这堂课的研究,你明确了????? ?,
你的收获与感受是?????????????? ????????,
你存在的疑惑之处有?????????????? ?。 课堂小结(课本)选做题必做题作 业A1.求过曲线y=x3-2x上的点(1,-1)的切线方程求过某点的曲线的切线方程时,除了要判断该点是否
在曲线上,还要分“该点是切点”和“该点不是切点”两种
情况进行讨论,解法复制。若设M(x0,y0)为曲线y=f(x)上
一点,则以M为切点的曲线的切线方程可设为
y-y0=f’(x)(x-x0),利用此切线方程可以简化解题,避免
疏漏。1.3.1 函数的单调性与导数(4).对数函数的导数:(5).指数函数的导数: (3).三角函数 : (1).常函数:(C)/ ? 0, (c为常数); (2).幂函数 : (xn)/ ? nxn?1
一、复习回顾:基本初等函数的导数公式函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时函数单调性判定单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,增函数减函数则 f(x) 在G上具有严格的单调性。G 称为单调区间G = ( a , b )二、复习引入:在(- ∞ ,0)和(0, +∞)
上分别是减函数。但在定义域上不是减函数。在(- ∞ ,1)上是减函数,在(1, +∞)上是增函数。在(- ∞,+∞)上是增函数概念回顾画出下列函数的图像,并根据图像指出每个函数的单调区间(1)函数的单调性也叫函数的增减性; (2)函数的单调性是对某个区间而言的,它是个局部概
念。这个区间是定义域的子集。(3)单调区间:针对自变量x而言的。
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间。 以前,我们用定义来判断函数的单调性.在假设x1 察: 下图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数 的图象, 图(2)表示高台跳水运动员的速度 v 随时间 t 变化的函数 的图象.
运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?aabbttvhOO ①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地, ②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,(1)(2)xyOxyOxyOxyOy = xy = x2y = x3 观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系. 在某个区间(a,b)内,如果 ,那么函数
在这个区间内单调递增; 如果 ,那么函数 在这个区间内单调递减.如果恒有 ,则 是常数。题1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数 的图象的大致形状.解: 当1 < x < 4 时, 可知 在此区间内单调递增; 当 x > 4 , 或 x < 1时, 可知 在此区间内单调递减; 当 x = 4 , 或 x = 1时, 综上, 函数 图象的大致形状如右图所示.题2 判断下列函数的单调性, 并求出单调区间:解:(1) 因为 , 所以因此, 函数 在 上单调递增.(2) 因为 , 所以当 , 即 时, 函数 单调递增;当 , 即 时, 函数 单调递减.题2 判断下列函数的单调性, 并求出单调区间:解:(3) 因为 , 所以因此, 函数 在 上单调递减.(4) 因为 , 所以 当 , 即 时, 函数 单调递增; 当 , 即 时, 函数 单调递减.1、求可导函数f(x)单调区间的步骤:
(1)求f’(x)
(2)解不等式f’(x)>0(或f’(x)<0)
(3)确认并指出递增区间(或递减区间)2、证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f’(x)
(2)确认f’(x)在(a,b)内的符号
(3)作出结论练习判断下列函数的单调性, 并求出单调区间:例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.练习2.函数 的图象如图所示, 试画出导函数 图象的大致形状练习3.讨论二次函数 的单调区间.解: 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是练习4.求证: 函数 在 内是减函数.解: 由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.一、求参数的取值范围增例2:求参数解:由已知得因为函数在(0,1]上单调递增增例2:在某个区间上, ,f(x)在这个区间上单调递增
(递减);但由f(x)在这个区间上单调递增(递减)而
仅仅得到 是不够的。还有可能导数等于0
也能使f(x)在这个区间上单调,
所以对于能否取到等号的问题需要单独验证
增例2:本题用到一个重要的转化:
例3:方程根的问题
求证:方程 只有一个根。作业:
已知函数f(x)=ax3+3x2-x+1在R上是减函数,求a的取值范围。
演示单调性导数的正负函数及图象切线斜率
的正负函数单调性与导数的关系?k>0k>0k<0k<0++--递增递减函数单调性与导数正负的关系注意:
应正确理解 “ 某个区间 ” 的含义, 它必是定义域内的某个区间。1.应用导数求函数的单调区间(选填:“增” ,“减” ,“既不是增函数,也不是减函数”)
(1) 函数y=x-3在[-3,5]上为__________函数。
(2) 函数 y = x2-3x 在[2,+∞)上为_____函数,
在(-∞,1]上为______函数,在[1,2]上为__
__________________________________函数。基础训练:应用举例增增减既不是增函数,也不是减函数求函数 的单调区间。变1:求函数 的单调区间。理解训练:解:的单调递增区间为单调递减区间为变3:求函数 的单调区间。解:解:总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳1°什么情况下,用“导数法” 求函数单调性、
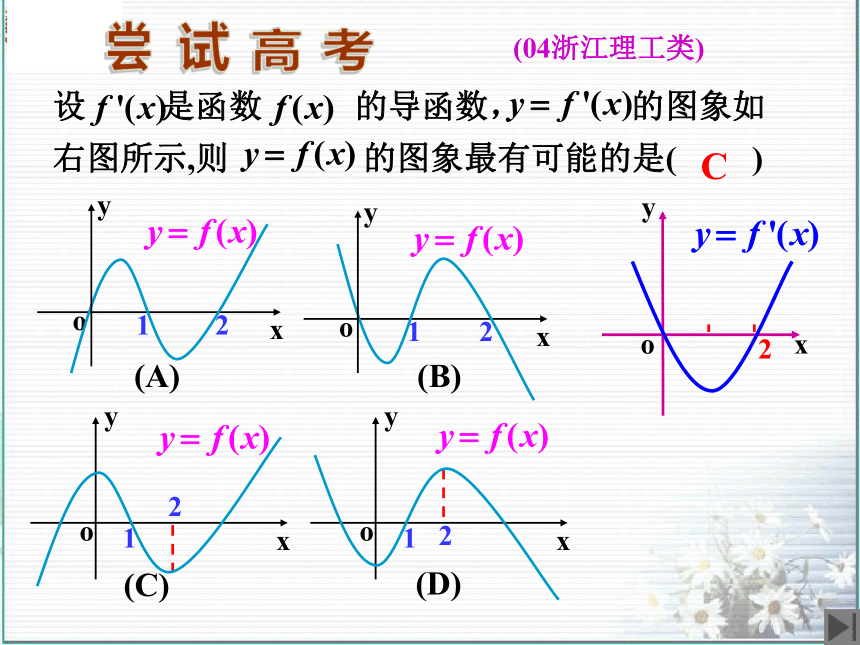
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归高考试(04年全国理)B尝已知导函数的下列信息:试画出函数 图象的大致形状。分析:2.应用导数信息确定函数大致图象已知导函数的下列信息:试画出函数 图象的大致形状。分析:2.应用导数信息确定函数大致图象解: 的大致形状如右图:(A)(B)(C)(D)C(04浙江理工类)高考试尝设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( ) 通过这堂课的研究,你明确了????? ?,
你的收获与感受是?????????????? ????????,
你存在的疑惑之处有?????????????? ?。 课堂小结(课本)选做题必做题作 业A1.求过曲线y=x3-2x上的点(1,-1)的切线方程求过某点的曲线的切线方程时,除了要判断该点是否
在曲线上,还要分“该点是切点”和“该点不是切点”两种
情况进行讨论,解法复制。若设M(x0,y0)为曲线y=f(x)上
一点,则以M为切点的曲线的切线方程可设为
y-y0=f’(x)(x-x0),利用此切线方程可以简化解题,避免
疏漏。1.3.1 函数的单调性与导数(4).对数函数的导数:(5).指数函数的导数: (3).三角函数 : (1).常函数:(C)/ ? 0, (c为常数); (2).幂函数 : (xn)/ ? nxn?1
一、复习回顾:基本初等函数的导数公式函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时函数单调性判定单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,增函数减函数则 f(x) 在G上具有严格的单调性。G 称为单调区间G = ( a , b )二、复习引入:在(- ∞ ,0)和(0, +∞)
上分别是减函数。但在定义域上不是减函数。在(- ∞ ,1)上是减函数,在(1, +∞)上是增函数。在(- ∞,+∞)上是增函数概念回顾画出下列函数的图像,并根据图像指出每个函数的单调区间(1)函数的单调性也叫函数的增减性; (2)函数的单调性是对某个区间而言的,它是个局部概
念。这个区间是定义域的子集。(3)单调区间:针对自变量x而言的。
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间。 以前,我们用定义来判断函数的单调性.在假设x1
运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?aabbttvhOO ①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地, ②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,(1)(2)xyOxyOxyOxyOy = xy = x2y = x3 观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系. 在某个区间(a,b)内,如果 ,那么函数
在这个区间内单调递增; 如果 ,那么函数 在这个区间内单调递减.如果恒有 ,则 是常数。题1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数 的图象的大致形状.解: 当1 < x < 4 时, 可知 在此区间内单调递增; 当 x > 4 , 或 x < 1时, 可知 在此区间内单调递减; 当 x = 4 , 或 x = 1时, 综上, 函数 图象的大致形状如右图所示.题2 判断下列函数的单调性, 并求出单调区间:解:(1) 因为 , 所以因此, 函数 在 上单调递增.(2) 因为 , 所以当 , 即 时, 函数 单调递增;当 , 即 时, 函数 单调递减.题2 判断下列函数的单调性, 并求出单调区间:解:(3) 因为 , 所以因此, 函数 在 上单调递减.(4) 因为 , 所以 当 , 即 时, 函数 单调递增; 当 , 即 时, 函数 单调递减.1、求可导函数f(x)单调区间的步骤:
(1)求f’(x)
(2)解不等式f’(x)>0(或f’(x)<0)
(3)确认并指出递增区间(或递减区间)2、证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f’(x)
(2)确认f’(x)在(a,b)内的符号
(3)作出结论练习判断下列函数的单调性, 并求出单调区间:例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.练习2.函数 的图象如图所示, 试画出导函数 图象的大致形状练习3.讨论二次函数 的单调区间.解: 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是练习4.求证: 函数 在 内是减函数.解: 由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.一、求参数的取值范围增例2:求参数解:由已知得因为函数在(0,1]上单调递增增例2:在某个区间上, ,f(x)在这个区间上单调递增
(递减);但由f(x)在这个区间上单调递增(递减)而
仅仅得到 是不够的。还有可能导数等于0
也能使f(x)在这个区间上单调,
所以对于能否取到等号的问题需要单独验证
增例2:本题用到一个重要的转化:
例3:方程根的问题
求证:方程 只有一个根。作业:
已知函数f(x)=ax3+3x2-x+1在R上是减函数,求a的取值范围。
