函数的导数
图片预览






文档简介
课件21张PPT。函数的导数函数单调性与导数正负的关系 (1) 如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)>0 右侧f /(x0)<0, 那么f(x0)是极大值【函数的极值与导数的关系】 (2) 如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)<0 右侧f /(x0)>0, 那么f(x0)是极小值左正右负极大值,
左负右正极小值求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f’(x)
(3)求方程f’(x)=0的根
(4)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(5)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
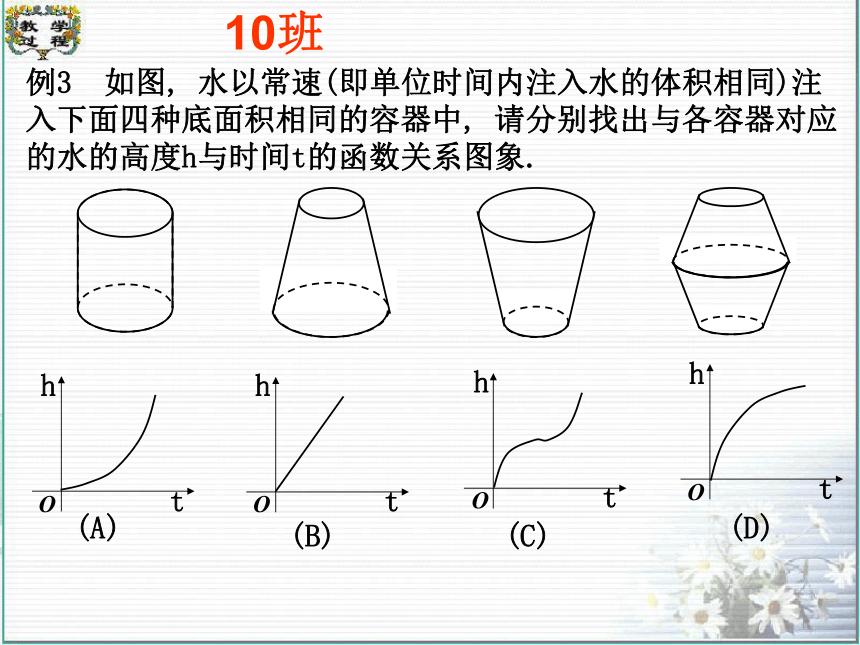
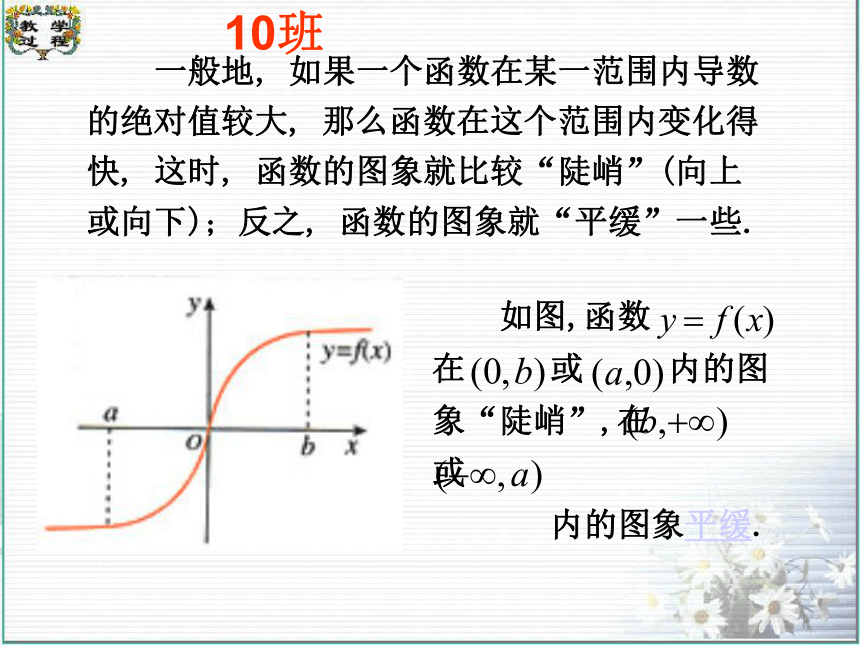
例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO10班 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
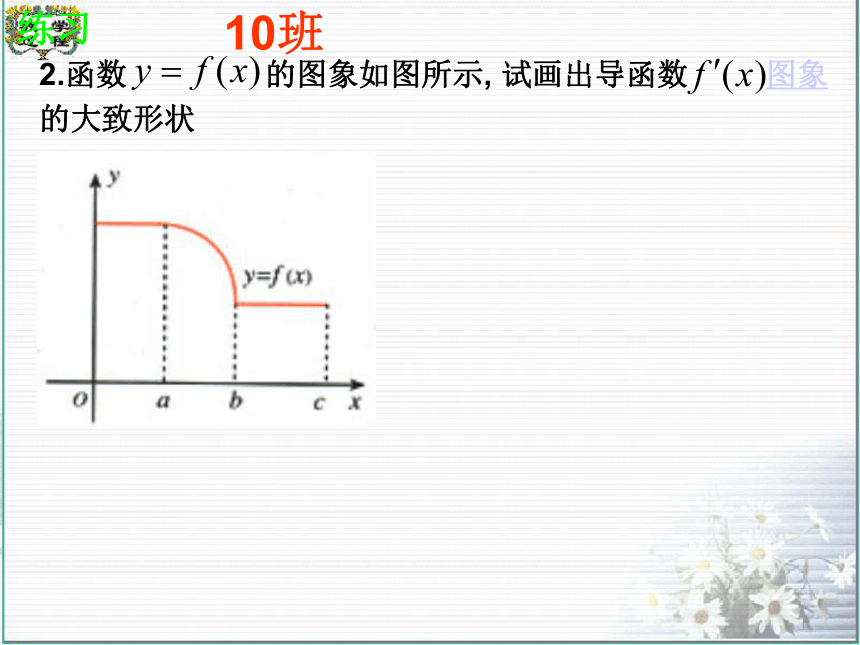
内的图象平缓.10班练习2.函数 的图象如图所示, 试画出导函数 图象的大致形状10班一、求参数的取值范围增例2:求参数解:由已知得因为函数在(0,1]上单调递增增例2:在某个区间上, ,f(x)在这个区间上单调递增
(递减);但由f(x)在这个区间上单调递增(递减)而
仅仅得到 是不够的。还有可能导数等于0
也能使f(x)在这个区间上单调,
所以对于能否取到等号的问题需要单独验证
增例2:本题用到一个重要的转化:
例3:方程根的问题
求证:方程 只有一个根。5 以下图形分别表示一个三次函数及其导数在同一坐标系中的图像,其中一定不正确的序号是( )XYOXYOXYOXYO(1)(2)(3)(4)A (3)(4) B (1)(3) C (2)(4) D(1)(2)A题型 1:图像与函数的极值题型2:含参数的函数分析:如果函数有极大值又有极小值,说明函数的导数的符号有从正变到负和从负变到正的时候,也就是说到导函数有两个相异的实根例1题型3: 求解析式若函数 在x=-1和x=3时有极值,则a=_______,b=_______-3-9a=-3,b=-9,c=2,极小值为-25 (2006年北京卷)已知函数在点 处取得极大值5,其导函数 的图像(如图)过点(1,0),(2,0), 求:
(1) 的值;(2)a,b,c的值;(1)由图像可知:(2) 在x=2处有极大值,求常数c的值 C=6
左负右正极小值求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f’(x)
(3)求方程f’(x)=0的根
(4)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(5)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO10班 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.10班练习2.函数 的图象如图所示, 试画出导函数 图象的大致形状10班一、求参数的取值范围增例2:求参数解:由已知得因为函数在(0,1]上单调递增增例2:在某个区间上, ,f(x)在这个区间上单调递增
(递减);但由f(x)在这个区间上单调递增(递减)而
仅仅得到 是不够的。还有可能导数等于0
也能使f(x)在这个区间上单调,
所以对于能否取到等号的问题需要单独验证
增例2:本题用到一个重要的转化:
例3:方程根的问题
求证:方程 只有一个根。5 以下图形分别表示一个三次函数及其导数在同一坐标系中的图像,其中一定不正确的序号是( )XYOXYOXYOXYO(1)(2)(3)(4)A (3)(4) B (1)(3) C (2)(4) D(1)(2)A题型 1:图像与函数的极值题型2:含参数的函数分析:如果函数有极大值又有极小值,说明函数的导数的符号有从正变到负和从负变到正的时候,也就是说到导函数有两个相异的实根例1题型3: 求解析式若函数 在x=-1和x=3时有极值,则a=_______,b=_______-3-9a=-3,b=-9,c=2,极小值为-25 (2006年北京卷)已知函数在点 处取得极大值5,其导函数 的图像(如图)过点(1,0),(2,0), 求:
(1) 的值;(2)a,b,c的值;(1)由图像可知:(2) 在x=2处有极大值,求常数c的值 C=6
