3.3函数的最大(小)值与导数
文档属性
| 名称 | 3.3函数的最大(小)值与导数 |

|
|
| 格式 | zip | ||
| 文件大小 | 532.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-14 00:00:00 | ||
图片预览







文档简介
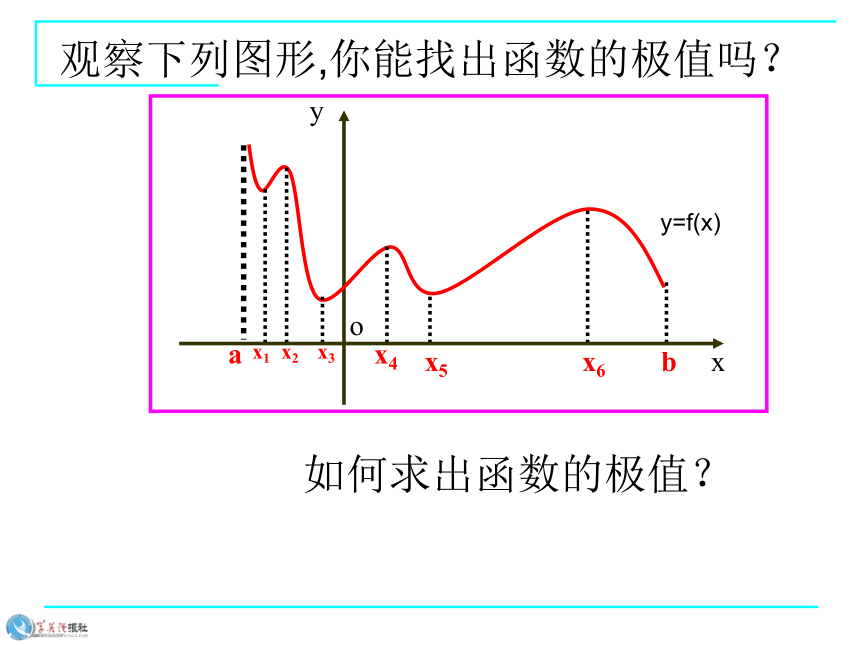
课件24张PPT。3.3.3函数的最大(小)值与导数观察下列图形,你能找出函数的极值吗?如何求出函数的极值?求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f’(x)
(3)求方程f’(x)=0的根
(4)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(5)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
左正右负极大值,
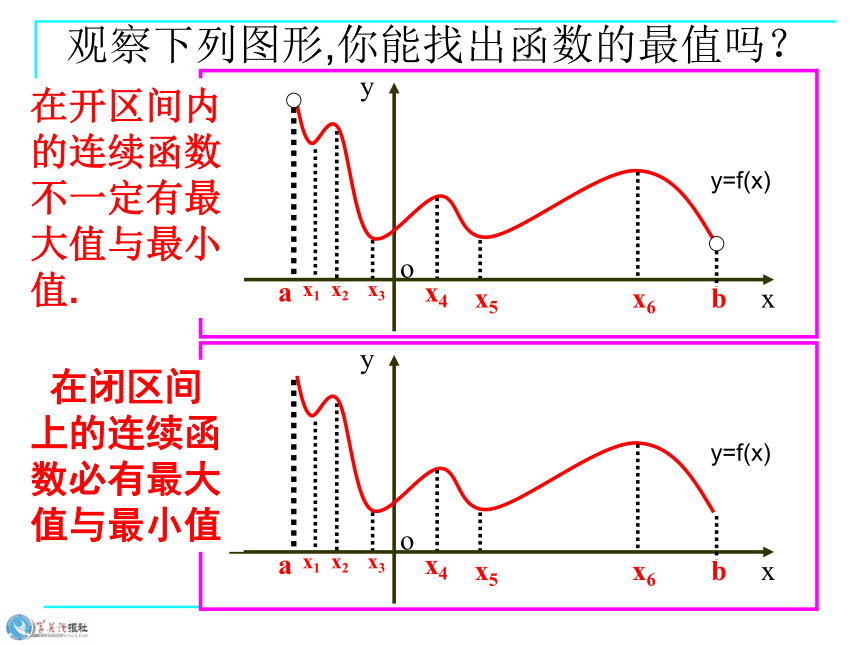
左负右正极小值观察下列图形,你能找出函数的最值吗?在开区间内的连续函数不一定有最大值与最小值. 在闭区间上的连续函数必有最大值与最小值如何求出函数在[a,b]上的最值? (2) 将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值. 求f(x)在闭区间[a,b]上的最值的步骤(1) 求f(x)在区间(a,b)内极值(极大值或极小值) 新课※典型例题1、求出所有导数为0的点;2、计算;3、比较确定最值。例1、1、2、求函数f(x)=x3 /3-4x+4在区间
[0,3] 内的最大值和最小值 ※动手试试求下列函数在给定区间上的最大值与最小值:4、f(x)=2x3-6x2+a x∈[-2,2]※典型例题反思:本题属于逆向探究题型;
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。 ※拓展提高我们知道,如果在闭区间【a,b】上函数y=f(x)的图像是一条连续不断的曲线,那么它必定有最大值和最小值;那么把闭区间【a,b】换成开区间(a,b)是否一定有最值呢? 不一定函数f(x)有一个极值点时,极值点必定是最值点。如果函数f(x)在开区间(a,b)上只有一个极值点,那么这个极值点必定是最值点。有两个极值点时,函数有无最值情况不定。※动手试试小结:1、基本知识2、基本思想一.是利用函数性质
二.是利用不等式
三.是利用导数 注:求函数最值的一般方法例1、求函数 在区间
[0,3] 内的最大值和最小值. 应用例2:(2005年北京)
已知函数f (x)=-x3+3x2+9x+a
(1)求f (x)的单调递减区间;
(2)若f (x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值. 应用 求函数f (x)=3x-x3 在区间 [-3,3]内的最大值和最小值. 练习一.是利用函数性质
二.是利用不等式
三.是利用导数 注:求函数最值的一般方法课本33页 练习
习题1.3 第6 题课后作业※典型例题反思:本题属于逆向探究题型;
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。 例2:(2005年北京)
已知函数f(x)=-x3+3x2+9x+a
1)求f(x)的单调递减区间;
2)若f(x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值.
(1)确定函数的定义域
(2)求函数的导数f’(x)
(3)求方程f’(x)=0的根
(4)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(5)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
左正右负极大值,
左负右正极小值观察下列图形,你能找出函数的最值吗?在开区间内的连续函数不一定有最大值与最小值. 在闭区间上的连续函数必有最大值与最小值如何求出函数在[a,b]上的最值? (2) 将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值. 求f(x)在闭区间[a,b]上的最值的步骤(1) 求f(x)在区间(a,b)内极值(极大值或极小值) 新课※典型例题1、求出所有导数为0的点;2、计算;3、比较确定最值。例1、1、2、求函数f(x)=x3 /3-4x+4在区间
[0,3] 内的最大值和最小值 ※动手试试求下列函数在给定区间上的最大值与最小值:4、f(x)=2x3-6x2+a x∈[-2,2]※典型例题反思:本题属于逆向探究题型;
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。 ※拓展提高我们知道,如果在闭区间【a,b】上函数y=f(x)的图像是一条连续不断的曲线,那么它必定有最大值和最小值;那么把闭区间【a,b】换成开区间(a,b)是否一定有最值呢? 不一定函数f(x)有一个极值点时,极值点必定是最值点。如果函数f(x)在开区间(a,b)上只有一个极值点,那么这个极值点必定是最值点。有两个极值点时,函数有无最值情况不定。※动手试试小结:1、基本知识2、基本思想一.是利用函数性质
二.是利用不等式
三.是利用导数 注:求函数最值的一般方法例1、求函数 在区间
[0,3] 内的最大值和最小值. 应用例2:(2005年北京)
已知函数f (x)=-x3+3x2+9x+a
(1)求f (x)的单调递减区间;
(2)若f (x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值. 应用 求函数f (x)=3x-x3 在区间 [-3,3]内的最大值和最小值. 练习一.是利用函数性质
二.是利用不等式
三.是利用导数 注:求函数最值的一般方法课本33页 练习
习题1.3 第6 题课后作业※典型例题反思:本题属于逆向探究题型;
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。 例2:(2005年北京)
已知函数f(x)=-x3+3x2+9x+a
1)求f(x)的单调递减区间;
2)若f(x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值.
