1.4生活中的优化问题举例

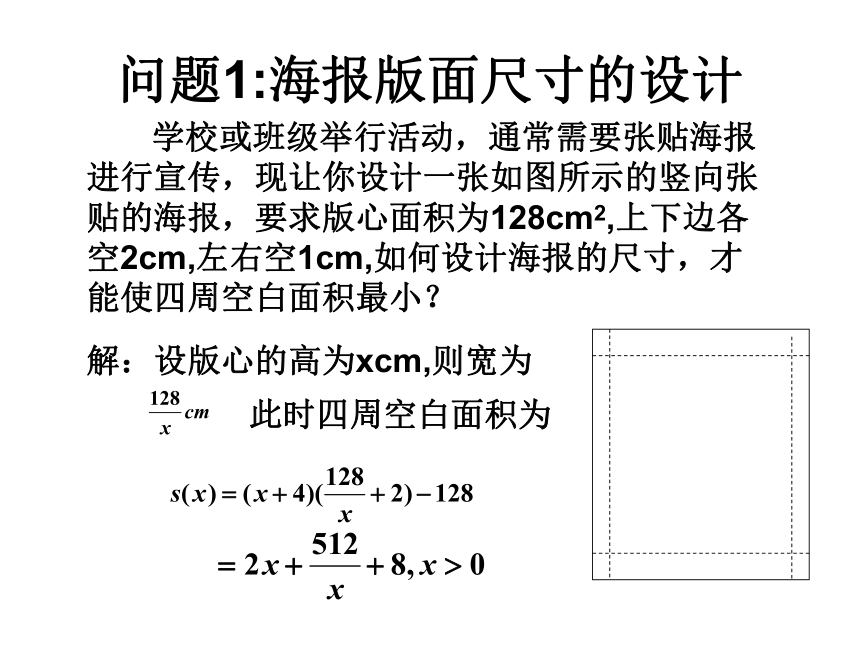
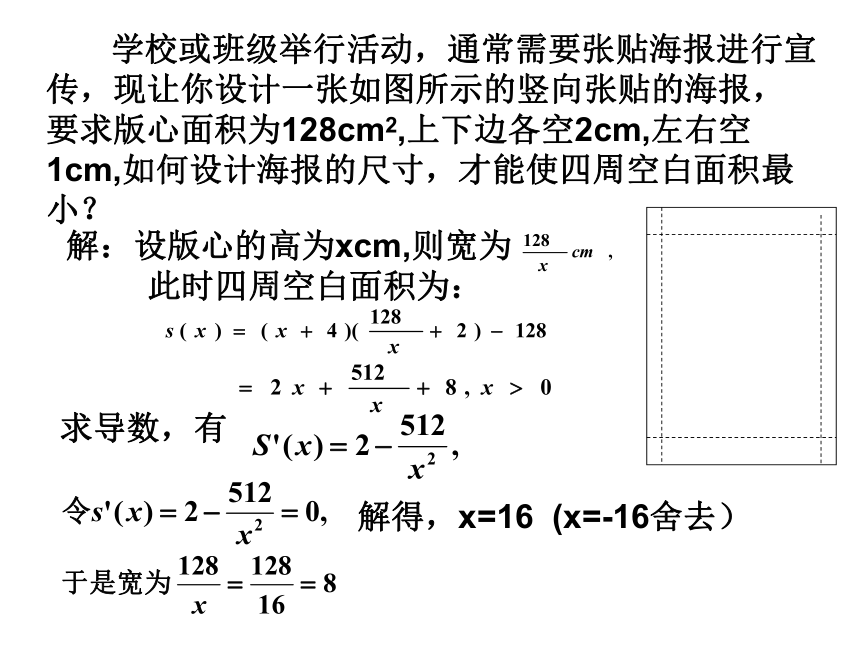
课件17张PPT。1.4 生活中的优化问题举例祁阳一中高二数学备课组 生活中经常遇到求利润最大、用料最省、效率最高等问题，这些问题通常称为优化问题，通过前面的学习，知道，导数是求函数最大（小）值的有力工具，本节我们运用导数，解决一些生活中的优化问题。问题1:海报版面尺寸的设计 学校或班级举行活动，通常需要张贴海报进行宣传，现让你设计一张如图所示的竖向张贴的海报，要求版心面积为128cm2,上下边各空2cm,左右空1cm,如何设计海报的尺寸，才能使四周空白面积最小？解：设版心的高为xcm,则宽为此时四周空白面积为 学校或班级举行活动，通常需要张贴海报进行宣传，现让你设计一张如图所示的竖向张贴的海报，要求版心面积为128cm2,上下边各空2cm,左右空1cm,如何设计海报的尺寸，才能使四周空白面积最小？解：设版心的高为xcm,则宽为此时四周空白面积为：求导数，有解得，x=16 (x=-16舍去）因此，x=16是函数s(x)的极小值点，也是最小值点。 所以，当版心高为16cm,宽为8cm时，能使四周空白面积最小。答：当版心高为16cm,宽为8cm时，海报四周空白面积最小。练习1、一条长为l的铁丝截成两段，分别
弯成两个正方形，要使两个正方形
的面积和最小，两段铁丝的长度分
别是多少？则两个正方形面积和为由问题的实际意义可知：问题2:饮料瓶大小对饮料公司利润有影响吗?你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些?你想从数学上知道它的道理吗?
是不是饮料瓶越大,饮料公司的利润越大? 某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.（１）瓶子半径多大时，能使每瓶饮料的利润最大？
（２）瓶子半径多大时，每瓶饮料的利润最小？解：由于瓶子的半径为r,所以每瓶饮料的利润为：例题:令解：由于瓶子的半径为r,所以每瓶饮料的利润为：令因此，当r>2时，f’(r)>0,它表示f(r)单调递增，即半径越大，利润越高；当r〈2时，f’(r)〈0,它表示f(r)单调递减，即半径越大，利润越低。（1）半径为2时，利润最小。这时f(2)<0,表示此种瓶内饮料的利润还不够瓶子的成本，此时利润是负值；（2）半径为6时，利润最大。解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(016000.由题意可知,当x过小(接近0)或过大(接近60)时,箱子的容积很小,因此,16000是最大值.答:当x=40cm时,箱子容积最大,最大容积是16000cm3.解:设圆柱的高为h,底半径为r,则表面积S=2πrh+2πr2.由V=πr2h,得 ,则令 ,解得 ,从而
,即h=2r.由于S(r)只有一个极值,所以它是最小值.答:当罐的高与底半径相等时,所用的材料最省.如何解决优化问题?优化问题优化问题的答案
用函数表示的数学问题用导数解决数学问题小结作业P37 习题1.4 A组 5,6