曲边梯形的面积课件

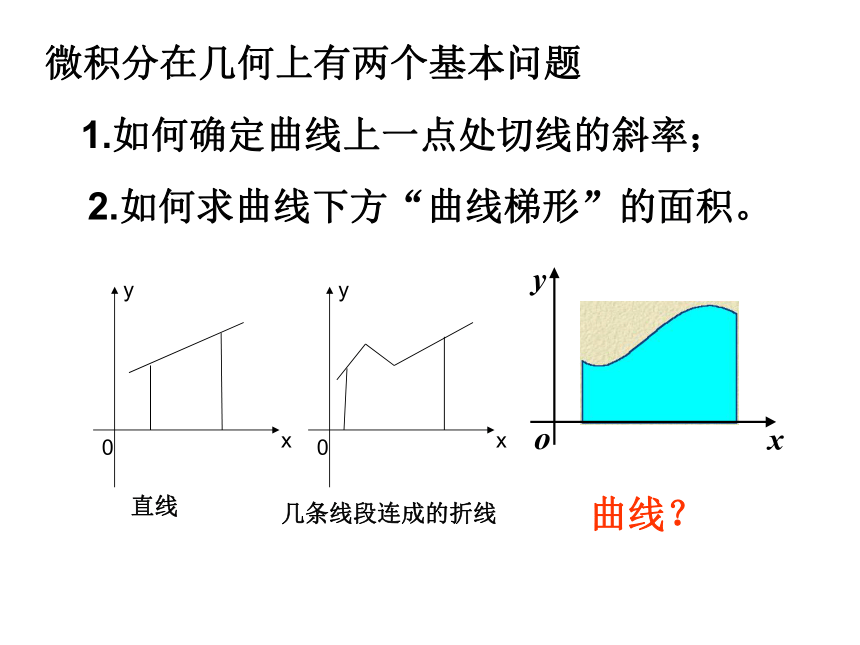
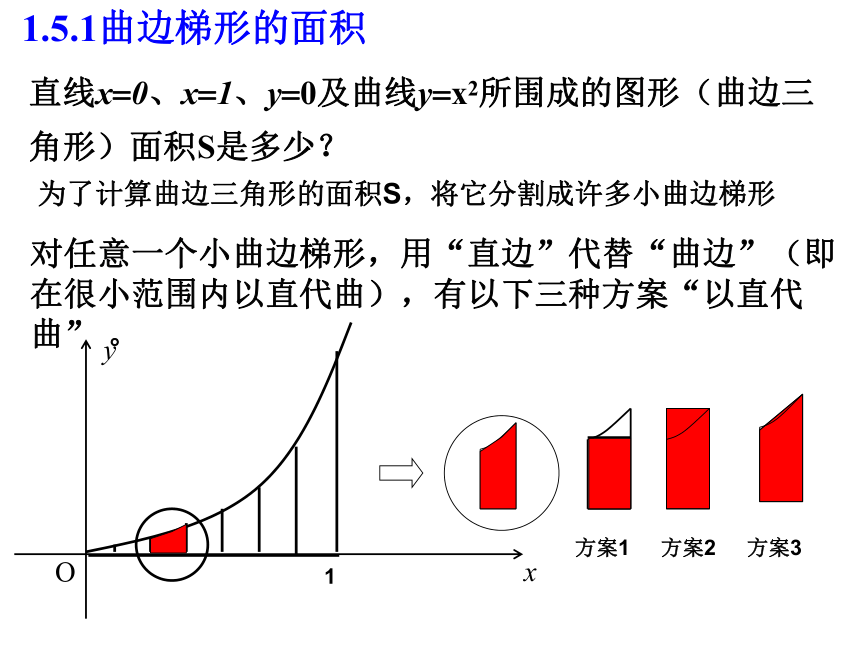
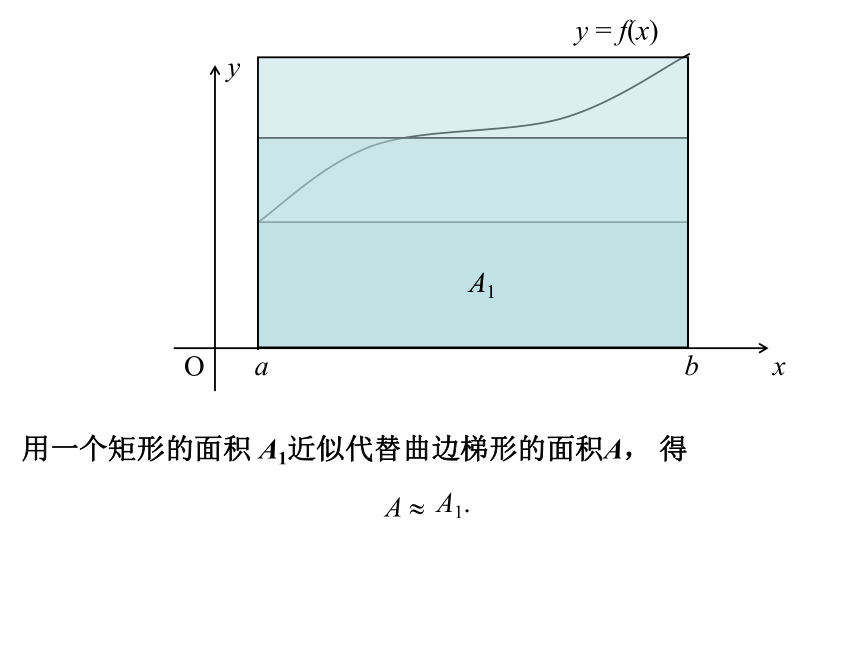
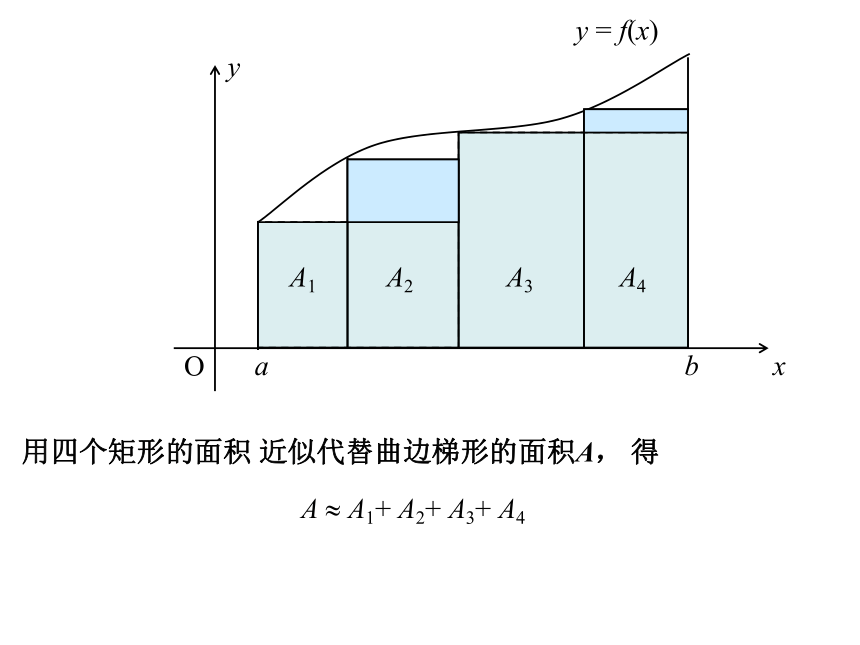
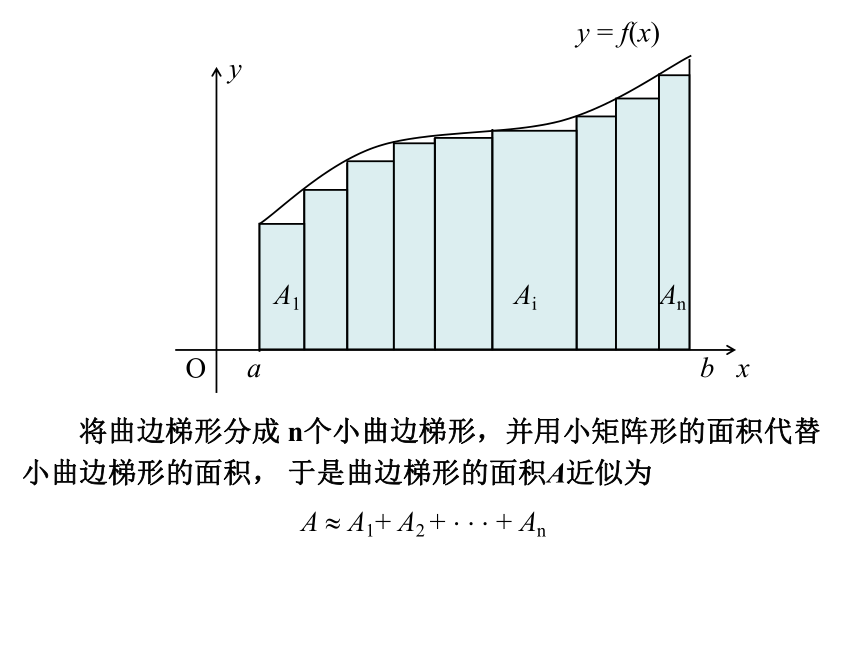
课件30张PPT。定积分微积分在几何上有两个基本问题1.如何确定曲线上一点处切线的斜率；2.如何求曲线下方“曲线梯形”的面积。直线几条线段连成的折线曲线？曲边梯形的面积1.5.1曲边梯形的面积直线x?0、x?1、y?0及曲线y?x2所围成的图形（曲边三角形）面积S是多少？方案1方案2方案3为了计算曲边三角形的面积S，将它分割成许多小曲边梯形对任意一个小曲边梯形，用“直边”代替“曲边”（即在很小范围内以直代曲），有以下三种方案“以直代曲” 。 y = f(x)用一个矩形的面积 A1近似代替曲边梯形的面积A， 得用两个矩形的面积 近似代替曲边梯形的面积A， 得A ? A1+ A2+ A3+ A4用四个矩形的面积 近似代替曲边梯形的面积A， 得A ? A1+ A2 + ? ? ? + An 将曲边梯形分成 n个小曲边梯形，并用小矩阵形的面积代替
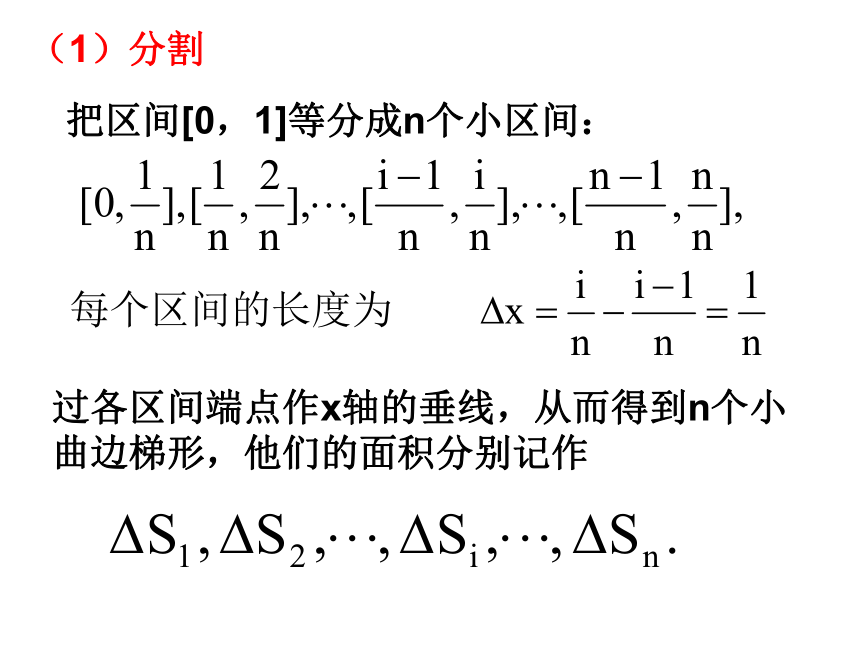
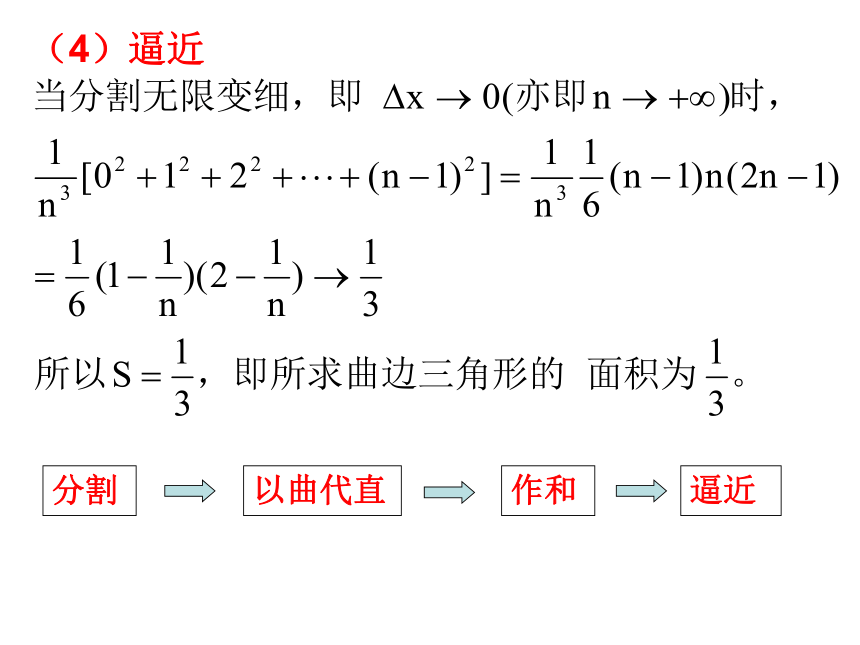
小曲边梯形的面积， 于是曲边梯形的面积A近似为分割越细，面积的近似值就越精确。当分割无限变细时，这个近似值就无限逼近所求曲边梯形的面积S。下面用第一种方案“以直代曲”的具体操作过程（1）分割把区间[0，1]等分成n个小区间：过各区间端点作x轴的垂线，从而得到n个小曲边梯形，他们的面积分别记作（2） 以直代曲（3）作和（4）逼近分割以曲代直作和逼近 当分点非常多（n非常大）时，可以认为f(x)在小区间上几乎没有变化（或变化非常小），从而可以取小区间内任意一点xi对应的函数值f(xi)作为小矩形一边的长，于是f(xi) △x来近似表示小曲边梯形的面积表示了曲边梯形面积的近似值演示 f(xi) f(x1) f(x2) f(xi)?xi在 [a, b]中任意插
入 n -1个分点．得n个小区间：
[xi?1 , xi ]
(i=1, 2 , · · ·, n)．把曲边梯形分成 n 个窄曲边梯形．任取xi ?[xi?1，xi ] ，以f (x i) Dxi近似代替第i个窄曲边梯形的面
积．区间[xi?1 , xi ]的长
度Dxi? xi ?xi?1 ．曲边梯形的面积近似为：A?曲边梯形的面积近似为：A?．观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。观察以下演示，注意当分割加细时，
矩形面积和与曲边梯形面积的关系。