向量的数乘(第一课)---苏教版[下学期]
文档属性
| 名称 | 向量的数乘(第一课)---苏教版[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 187.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-29 21:08:00 | ||
图片预览



文档简介
课件11张PPT。 实数与向量的积学习目标
1.理解向量数乘的含义
2.掌握向量数乘的运算律
3.体验从数与形两个角度研究向量数乘
的含义和运算律
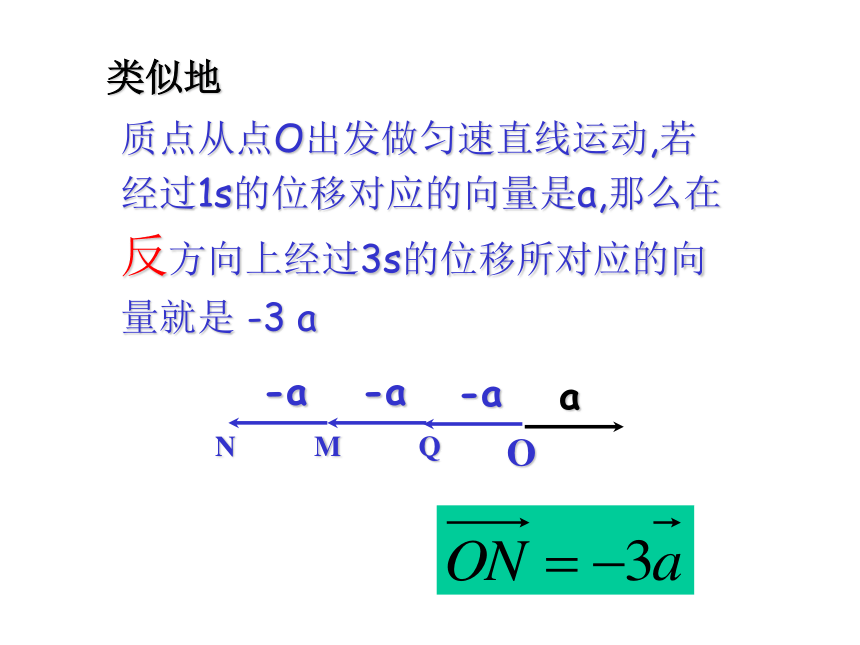
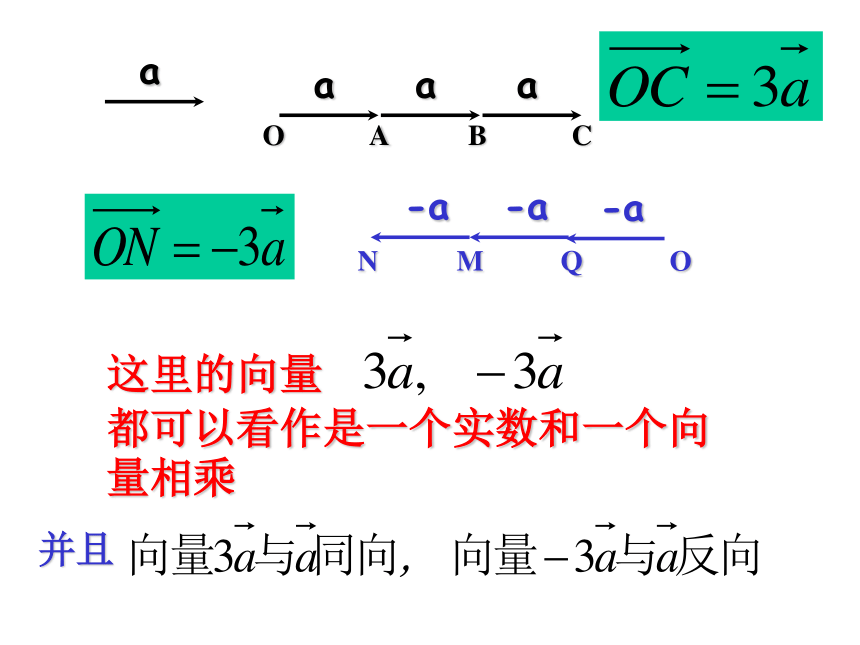
第一课知识再现:试作出: a+a+a 已知非零向量 a (如图)OABC例题的模型:质点从点O出发做匀速直线运动,若经过1s的位移对应的向量是a,那么在同方向上经过3s的位移所对应的向量就是3 a类似地OQMN质点从点O出发做匀速直线运动,若经过1s的位移对应的向量是a,那么在反方向上经过3s的位移所对应的向量就是 -3 a
这里的向量
都可以看作是一个实数和一个向量相乘并且定义:一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘. 回答:已知λ∈R, a为非零向量,则下列命题正确的是 ( )
A.当λ>0时, λa与a方向一定相同
B. 当λ<0时, λa与a方向不一 定相反
C. |λa|=|λ|a D|λa|=|λ|a
一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘. 回答:已知 |a|=1,|b|=3,
(1)若向量a与向量b同向,则b= a
(2)若向量a与向量b共线,则a= b
3向量共线:同向,反向(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。= 你会吗运算吗?
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)答案:-12a5b-a+5b-2c回答:课堂练习(强化训练):
合作或自主完成以下作业(见小卷)
参考答案
一、向量数乘的概念你清楚了吗?
一般地,实数λ与向量a的积是一个向量,记作λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘.二 向量数乘的运算律你知道吗? 设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a ②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
课外作业P68
5,6,8,9
1.理解向量数乘的含义
2.掌握向量数乘的运算律
3.体验从数与形两个角度研究向量数乘
的含义和运算律
第一课知识再现:试作出: a+a+a 已知非零向量 a (如图)OABC例题的模型:质点从点O出发做匀速直线运动,若经过1s的位移对应的向量是a,那么在同方向上经过3s的位移所对应的向量就是3 a类似地OQMN质点从点O出发做匀速直线运动,若经过1s的位移对应的向量是a,那么在反方向上经过3s的位移所对应的向量就是 -3 a
这里的向量
都可以看作是一个实数和一个向量相乘并且定义:一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘. 回答:已知λ∈R, a为非零向量,则下列命题正确的是 ( )
A.当λ>0时, λa与a方向一定相同
B. 当λ<0时, λa与a方向不一 定相反
C. |λa|=|λ|a D|λa|=|λ|a
一般地,实数λ与向量a的积是一个向量,记作
λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘. 回答:已知 |a|=1,|b|=3,
(1)若向量a与向量b同向,则b= a
(2)若向量a与向量b共线,则a= b
3向量共线:同向,反向(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。= 你会吗运算吗?
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)答案:-12a5b-a+5b-2c回答:课堂练习(强化训练):
合作或自主完成以下作业(见小卷)
参考答案
一、向量数乘的概念你清楚了吗?
一般地,实数λ与向量a的积是一个向量,记作λa,它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0时, λa=0
实数λ与向量a相乘,叫做向量的数乘.二 向量数乘的运算律你知道吗? 设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a ②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
课外作业P68
5,6,8,9
