黑龙江省哈尔滨市香坊区第三十五中学2022-2023学年八年级下学期期中测试数学试题(五四制)(PDF版 含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区第三十五中学2022-2023学年八年级下学期期中测试数学试题(五四制)(PDF版 含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 22:17:17 | ||
图片预览



文档简介
2022-2023 学年度下学期哈尔滨市三十五中学校
八年级下学科期中测试题
一.选择题(每题 3 分,共 30 分)
1.由下列线段 a,b,c可以组成直角三角形的是( ).
A. a 1,b 2,c 3 B. a b 1,c 3
B. a 4,b 5,c 6 D. a 2,b 2 3,c 4
2.等腰三角形的腰长为 10,底边长为 12,则底边上的高为( )
A. 13 B . 8 C . 25 D. 64
3.矩形具有而平行四边形不具有的性质是( )
A.对边相等 B . 对角相等 C .对角线相等 D.对角线互相平分
4.△ABC 的三边中点为 D、E、F,,且△DEF 的周长为 4,则△ABC 的周长是( )
A.4 B . 8 C .6 D.16
5.下列条件中,能判定四边形 ABCD 是平行四边形的是( )
A.AB∥CD ,AD=BC B . AB∥CD ,AD∥BC C .∠A=∠B,∠C=∠D D.AB=AD,BC=CD
6.如图,菱形 ABCD 中,对角线 AC、BD 相交于点 O,H 为 AD 边中点,菱形 ABCD 的周长为 32,
则 OH 的长等于( )
A.4 B.8 C.16 D.18
C S2
S3
A B
S1
6 题 7 题 8题 9 题
7.如图,以 Rt△ABC 的三边为边长向外作正方形,三个正方形的面积分别为 S1 、 S2 、 S3 ,若
S1 13, S2 12,则 S3 的值为( ).
A.1 B.5 C.25 D. 144
8.如图,将一个边长分别为 4,8 的矩形纸片 ABCD 折叠,使 C 与 A 重合,则折痕 EF 的长( )
A. 3 B. 2 3 C. 5 D. 2 5
9.如图,有一个平行四边形 ABCD 与一正方形 CEFG,其中 E点在 AD 上,若∠ECD=35°,∠AEF=15°,
则∠B 的度数为( )
A. 50 B. 55 C. 70 D. 75
10.如图,菱形 ABCD 中,∠A=60°,E,F 分别是边 AB,AD 的中点,DE,BF
相交于 G,连接 CG,以下结论正确的有( )个
第 1 页 共 6页
3
(1)∠BGD=120°(2)S△ADE:S△GBC=2:3 (3)BG+DG=CG 4 S
2
( ) 菱形ABCD= AB
2
A. 1 B. 2 C. 3 D. 4
二、填空题(每题 3 分,共 30 分)
11.在△ABC 中,∠C=90°,若 AC=BC=2,则 AB=
12.平行四边形 ABCD 中,∠A=45°,则∠B 的度数为
13.平行四边形 ABCD 的周长为 30,对角线 AC 与 BD 相交于点 O,△ABC 的周长为 20,
则 CO=
14.如图,一棵高为 8 米的大树离地面 3 米处折断,则树顶部落在距离树底部 米处.
14 题 15 题 16 题
15.如图,已知正方形 ABCD 的边长为 4,对角线 AC 与 BD 相交于点 O,点 E 在 DC 边的延长线上.若
∠CAE=15°,则 AE 的长度为
16. 如图,四边形 ABCD 是菱形,AC=8,DB=6,DH⊥AB 于 H,则 DH 的长度为 .
17.如图,已知正方形 ABCD 的边长为 8,点 E为 CD 中点,点 P 在对角线 AC 上,且 PB⊥PE,则 PC
的长为 .
17 题 18 题 20 题
18. 如图,AD 为△ABC 的高,E 为 AD 边上一点,M,N 分别为 BE,AC 的中点,若 AE=6,BC=8,则 MN
的长是 。
19. 在矩形 ABCD 中,AB=4,AD=8,P 为对角线 BD 垂直平分线上一点,且 PD=5,则 AP 的长是 。
20.如图,△ABC 中,∠BAC=90°,AB=AC,D,E 分别在 AB,AC 上,且 CE=AD,过点 E作 EF⊥CD,垂足为
F,连接 AF,BF,若 CF=1,BF= 13 ,则 AF= .
三、解答题(21 题,22 题各 7 分,23 题,24 题各 8 分,25,26,27 题各 10 分)
1 x2 1
21.化简并求值:(1 ) 2 ,其中 x=3x 2 x 4x 12
第 2 页 共 6页
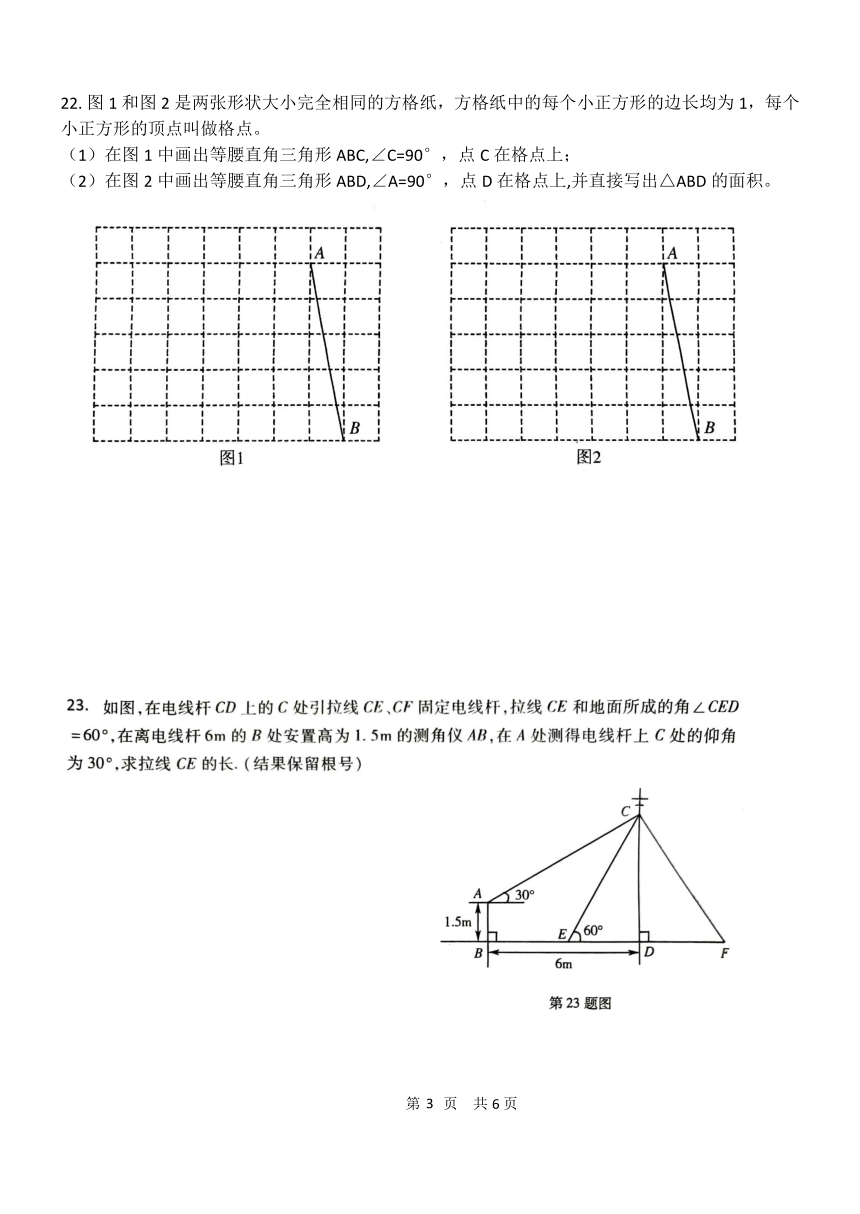
22.图 1 和图 2 是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为 1,每个
小正方形的顶点叫做格点。
(1)在图 1 中画出等腰直角三角形 ABC,∠C=90°,点 C 在格点上;
(2)在图 2 中画出等腰直角三角形 ABD,∠A=90°,点 D在格点上,并直接写出△ABD 的面积。
第 3 页 共 6页
24.如图,△ABC 中,D、E、F 分别为 AB、AC、BC 边中点,连接 AF.DE 相交于 G,若 N 为 CF 中点
(1)求证:四边形 GFNE 为平行四边形
(2)连接 DN,若 DN=DB,请直接写出图中与线段 EN 相等的所有线段
25. 倡导健康生活,推进全民健身。某社区要购进 A.B 两种型号的健身器材若干套,A.B 两种型号
的健身器材的购买单价分别为每套 310 元,460 元,且每种型号健身器材必须整套购买。
(1)若购买 A.B 两种型号的健身器材共 50 套,且恰好支出 20000 元,求 A.B 两种型号的健身器材
各购买多少套?
(2)若购买 A.B 两种型号的健身器材共 50 套,且支出不超过 18000 元,求 A 型号健身器材至少要
购买多少套?
第 4 页 共 6页
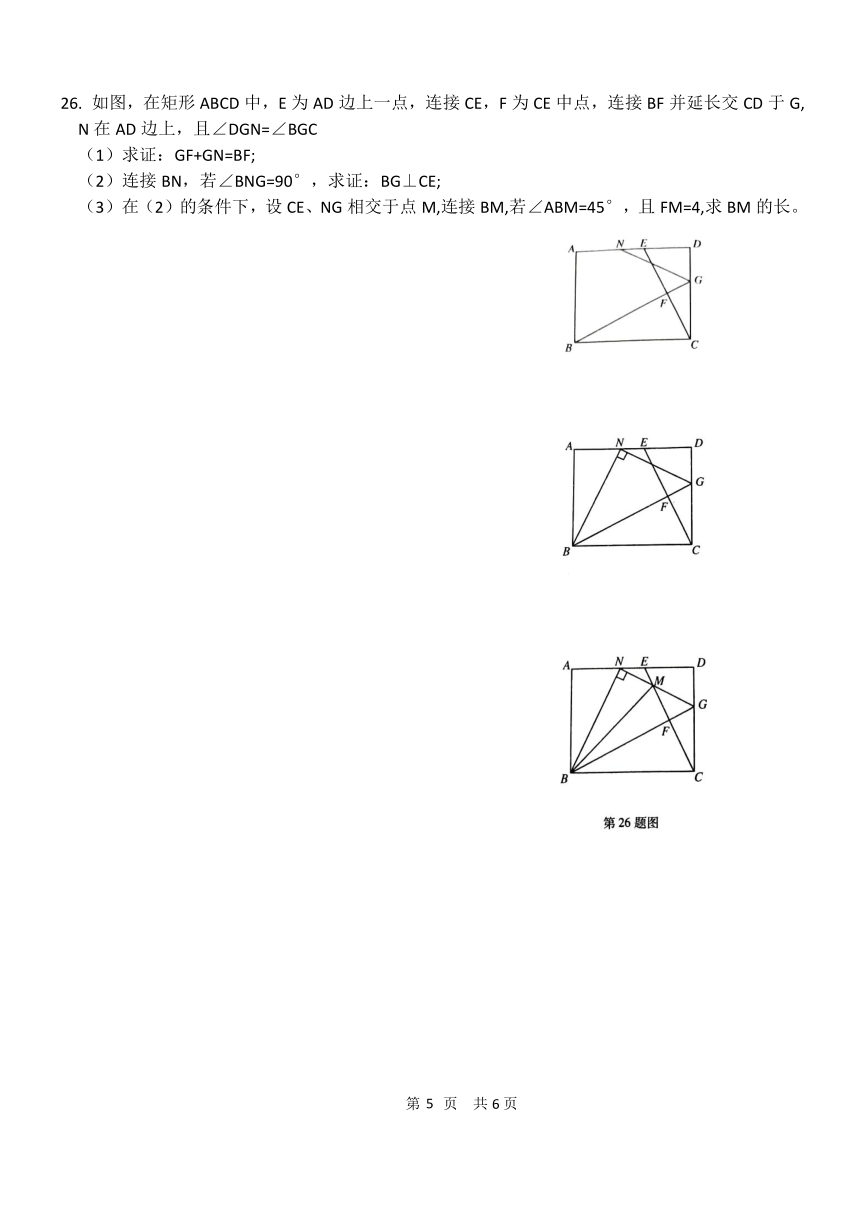
26. 如图,在矩形 ABCD 中,E为 AD 边上一点,连接 CE,F 为 CE 中点,连接 BF 并延长交 CD 于 G,
N 在 AD 边上,且∠DGN=∠BGC
(1)求证:GF+GN=BF;
(2)连接 BN,若∠BNG=90°,求证:BG⊥CE;
(3)在(2)的条件下,设 CE、NG 相交于点 M,连接 BM,若∠ABM=45°,且 FM=4,求 BM 的长。
第 5 页 共 6页
27. 如图,在平面直角坐标系中 A(-3,0),B(0,4),四边形 ADCB 为平行四边形,点 D 在 x 轴上,且 AD=8,
动点 P 从原点 O 出发,以每秒 1 个单位的速度沿 x 轴正方向运动,同时,动点 Q从原点 O 出发,
以每秒 2 个单位的速度沿 y 轴正方向运动
(1)求点 C 的坐标;
(2)当运动时间 t 为何值时,以 P,B,C,D 为顶点的四边形面积为 20;
(3)在线段 BC 上是否存在点 R,使△OPQ 与△BQR 全等?若存在,求出点 R 的坐标,若不存在,
说明理由。
第 6 页 共 6页
八年级下学科期中测试题
一.选择题(每题 3 分,共 30 分)
1.由下列线段 a,b,c可以组成直角三角形的是( ).
A. a 1,b 2,c 3 B. a b 1,c 3
B. a 4,b 5,c 6 D. a 2,b 2 3,c 4
2.等腰三角形的腰长为 10,底边长为 12,则底边上的高为( )
A. 13 B . 8 C . 25 D. 64
3.矩形具有而平行四边形不具有的性质是( )
A.对边相等 B . 对角相等 C .对角线相等 D.对角线互相平分
4.△ABC 的三边中点为 D、E、F,,且△DEF 的周长为 4,则△ABC 的周长是( )
A.4 B . 8 C .6 D.16
5.下列条件中,能判定四边形 ABCD 是平行四边形的是( )
A.AB∥CD ,AD=BC B . AB∥CD ,AD∥BC C .∠A=∠B,∠C=∠D D.AB=AD,BC=CD
6.如图,菱形 ABCD 中,对角线 AC、BD 相交于点 O,H 为 AD 边中点,菱形 ABCD 的周长为 32,
则 OH 的长等于( )
A.4 B.8 C.16 D.18
C S2
S3
A B
S1
6 题 7 题 8题 9 题
7.如图,以 Rt△ABC 的三边为边长向外作正方形,三个正方形的面积分别为 S1 、 S2 、 S3 ,若
S1 13, S2 12,则 S3 的值为( ).
A.1 B.5 C.25 D. 144
8.如图,将一个边长分别为 4,8 的矩形纸片 ABCD 折叠,使 C 与 A 重合,则折痕 EF 的长( )
A. 3 B. 2 3 C. 5 D. 2 5
9.如图,有一个平行四边形 ABCD 与一正方形 CEFG,其中 E点在 AD 上,若∠ECD=35°,∠AEF=15°,
则∠B 的度数为( )
A. 50 B. 55 C. 70 D. 75
10.如图,菱形 ABCD 中,∠A=60°,E,F 分别是边 AB,AD 的中点,DE,BF
相交于 G,连接 CG,以下结论正确的有( )个
第 1 页 共 6页
3
(1)∠BGD=120°(2)S△ADE:S△GBC=2:3 (3)BG+DG=CG 4 S
2
( ) 菱形ABCD= AB
2
A. 1 B. 2 C. 3 D. 4
二、填空题(每题 3 分,共 30 分)
11.在△ABC 中,∠C=90°,若 AC=BC=2,则 AB=
12.平行四边形 ABCD 中,∠A=45°,则∠B 的度数为
13.平行四边形 ABCD 的周长为 30,对角线 AC 与 BD 相交于点 O,△ABC 的周长为 20,
则 CO=
14.如图,一棵高为 8 米的大树离地面 3 米处折断,则树顶部落在距离树底部 米处.
14 题 15 题 16 题
15.如图,已知正方形 ABCD 的边长为 4,对角线 AC 与 BD 相交于点 O,点 E 在 DC 边的延长线上.若
∠CAE=15°,则 AE 的长度为
16. 如图,四边形 ABCD 是菱形,AC=8,DB=6,DH⊥AB 于 H,则 DH 的长度为 .
17.如图,已知正方形 ABCD 的边长为 8,点 E为 CD 中点,点 P 在对角线 AC 上,且 PB⊥PE,则 PC
的长为 .
17 题 18 题 20 题
18. 如图,AD 为△ABC 的高,E 为 AD 边上一点,M,N 分别为 BE,AC 的中点,若 AE=6,BC=8,则 MN
的长是 。
19. 在矩形 ABCD 中,AB=4,AD=8,P 为对角线 BD 垂直平分线上一点,且 PD=5,则 AP 的长是 。
20.如图,△ABC 中,∠BAC=90°,AB=AC,D,E 分别在 AB,AC 上,且 CE=AD,过点 E作 EF⊥CD,垂足为
F,连接 AF,BF,若 CF=1,BF= 13 ,则 AF= .
三、解答题(21 题,22 题各 7 分,23 题,24 题各 8 分,25,26,27 题各 10 分)
1 x2 1
21.化简并求值:(1 ) 2 ,其中 x=3x 2 x 4x 12
第 2 页 共 6页
22.图 1 和图 2 是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为 1,每个
小正方形的顶点叫做格点。
(1)在图 1 中画出等腰直角三角形 ABC,∠C=90°,点 C 在格点上;
(2)在图 2 中画出等腰直角三角形 ABD,∠A=90°,点 D在格点上,并直接写出△ABD 的面积。
第 3 页 共 6页
24.如图,△ABC 中,D、E、F 分别为 AB、AC、BC 边中点,连接 AF.DE 相交于 G,若 N 为 CF 中点
(1)求证:四边形 GFNE 为平行四边形
(2)连接 DN,若 DN=DB,请直接写出图中与线段 EN 相等的所有线段
25. 倡导健康生活,推进全民健身。某社区要购进 A.B 两种型号的健身器材若干套,A.B 两种型号
的健身器材的购买单价分别为每套 310 元,460 元,且每种型号健身器材必须整套购买。
(1)若购买 A.B 两种型号的健身器材共 50 套,且恰好支出 20000 元,求 A.B 两种型号的健身器材
各购买多少套?
(2)若购买 A.B 两种型号的健身器材共 50 套,且支出不超过 18000 元,求 A 型号健身器材至少要
购买多少套?
第 4 页 共 6页
26. 如图,在矩形 ABCD 中,E为 AD 边上一点,连接 CE,F 为 CE 中点,连接 BF 并延长交 CD 于 G,
N 在 AD 边上,且∠DGN=∠BGC
(1)求证:GF+GN=BF;
(2)连接 BN,若∠BNG=90°,求证:BG⊥CE;
(3)在(2)的条件下,设 CE、NG 相交于点 M,连接 BM,若∠ABM=45°,且 FM=4,求 BM 的长。
第 5 页 共 6页
27. 如图,在平面直角坐标系中 A(-3,0),B(0,4),四边形 ADCB 为平行四边形,点 D 在 x 轴上,且 AD=8,
动点 P 从原点 O 出发,以每秒 1 个单位的速度沿 x 轴正方向运动,同时,动点 Q从原点 O 出发,
以每秒 2 个单位的速度沿 y 轴正方向运动
(1)求点 C 的坐标;
(2)当运动时间 t 为何值时,以 P,B,C,D 为顶点的四边形面积为 20;
(3)在线段 BC 上是否存在点 R,使△OPQ 与△BQR 全等?若存在,求出点 R 的坐标,若不存在,
说明理由。
第 6 页 共 6页
同课章节目录
