人教版六年级上册第八单元数学广角数与形同步教案
文档属性
| 名称 | 人教版六年级上册第八单元数学广角数与形同步教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 21:50:15 | ||
图片预览

文档简介
《数与形》教学设计
一、教学内容
人教版数学六年级上册第107页例1。
二、教学目标
1.在解决“形”的问题情境中,借助“数”来直观感受与“形”之间的关系,体会有时“形”与“数”能互相解释,并能借助“数”解决一些与“形”相关的问题。
2.经历运用数与形结合来分析思考数学问题的过程,在“观察—猜想—关联—操作—论证—归纳”等数学活动中,通过撬动数与形的关系链接发展数学思 考,感悟数形结合的思想方法,提高问题解决的能力。
3.感悟数形结合的思考价值,培养独立思考、合作交流、反思质疑的习惯,感受到问题研究的乐趣,喜欢数学,喜欢思考。
三、教学重难点
借助“数”感受与“形”之间的关系,用数形结合的思想方法解决数学问题。
五、教学过程
(一)课前导入
师:同学们,你们认为数学是什么?
课件出示:数学是研究数量关系和空间形式的科学。
板书:数 与 形
师:今天我们就来研究数与形。大家看到这个题目,有什么问题吗?
预设:哪些数?什么图形?它们有什么关系/联系?(二)互动新授
1.数形互猜,初步感受
依次出示三个图形:
(1)
(2)
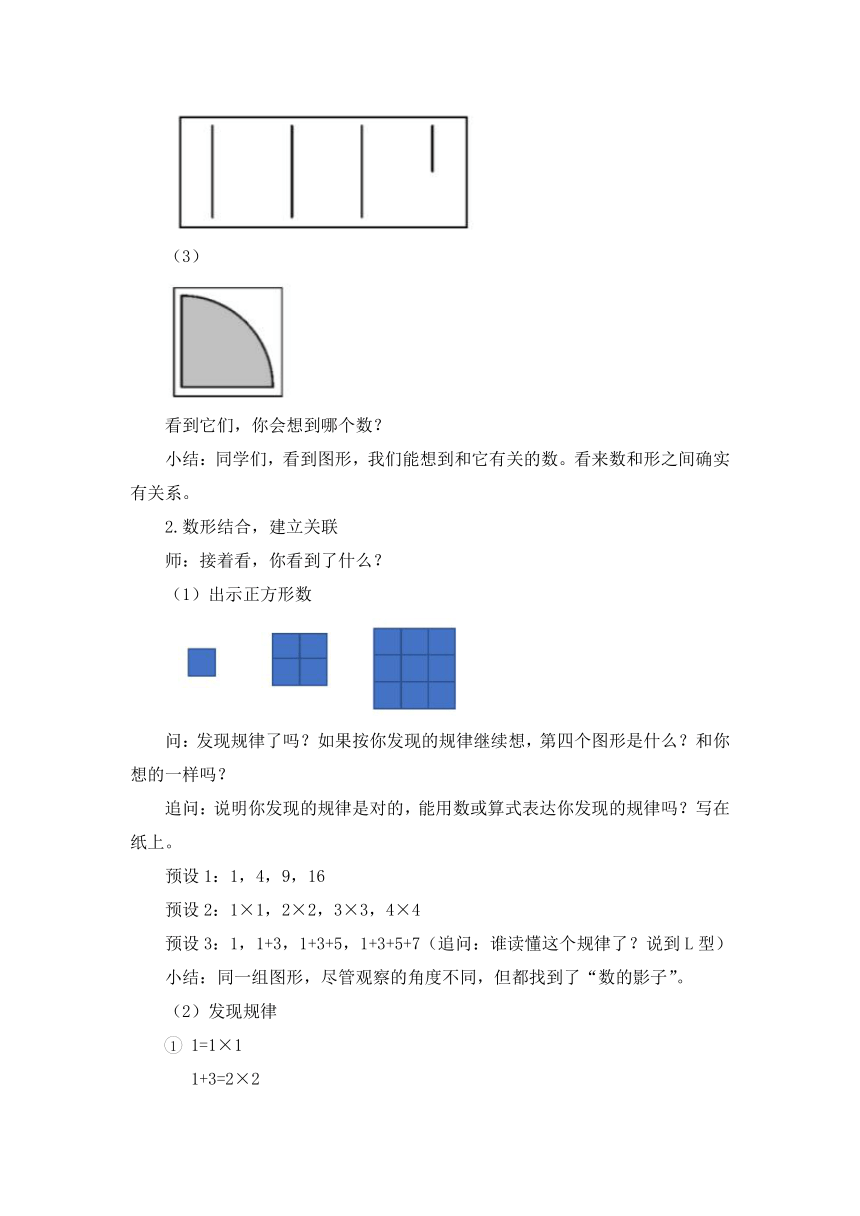
(3)
看到它们,你会想到哪个数?
小结:同学们,看到图形,我们能想到和它有关的数。看来数和形之间确实有关系。
2.数形结合,建立关联
师:接着看,你看到了什么?
(1)出示正方形数
问:发现规律了吗?如果按你发现的规律继续想,第四个图形是什么?和你想的一样吗?
追问:说明你发现的规律是对的,能用数或算式表达你发现的规律吗?写在纸上。
预设1:1,4,9,16
预设2:1×1,2×2,3×3,4×4
预设3:1,1+3,1+3+5,1+3+5+7(追问:谁读懂这个规律了?说到L型)
小结:同一组图形,尽管观察的角度不同,但都找到了“数的影子”。
(2)发现规律
1=1×1
1+3=2×2
1+3+5=3×3
1+3+5+7=4×4
为什么?1,2,3,4分别在哪里?
1,1+3,1+3+5,1+3+5+7是从1开始的连续奇数相加。
追问:能继续说吗?说的完吗?
有几个加数相加就是几的平方。
课件逐步出示:
小结:这么复杂的算式被这个简单的图形就表示了,说明数与形之间不仅有关系,还很紧密。
2.以形助数,深化联系
(1)出示:
1+3+5+7+9+11+13=( )
( ) =8^2
1+3+5+7+5+3+1=
追问:这个算式是怎么样的图形呢?
预设1:分成两半:1+3+5+7和1+3+5,4^2+3^2=25=5^2,5的平方怎么来的?
预设2:看成1+3+5+7+9
(2)3^2+4^2=5^2
视频解释以下公式。
(四)拓展贯通,感悟价值
过渡:其实,像这样借助数与形紧密关联的方法来解决问题的情况在我们小学阶段以往的数学学习中并不陌生。回想一下,在哪里见过?举例说明。
介绍:
(五)分层练习,回顾总结
1.出示:长方体沙坑,一辆载重 1.5 吨卡车。
你能提出什么数学问题?
出示:沙坑数据:长、宽、高分别是 2.5m、4m、1.5m。
汽车数据:长、宽、高分别是3m、7m、0.7m。
2.通过今天的学习,关于数与形,你们还有什么疑问吗?
一、教学内容
人教版数学六年级上册第107页例1。
二、教学目标
1.在解决“形”的问题情境中,借助“数”来直观感受与“形”之间的关系,体会有时“形”与“数”能互相解释,并能借助“数”解决一些与“形”相关的问题。
2.经历运用数与形结合来分析思考数学问题的过程,在“观察—猜想—关联—操作—论证—归纳”等数学活动中,通过撬动数与形的关系链接发展数学思 考,感悟数形结合的思想方法,提高问题解决的能力。
3.感悟数形结合的思考价值,培养独立思考、合作交流、反思质疑的习惯,感受到问题研究的乐趣,喜欢数学,喜欢思考。
三、教学重难点
借助“数”感受与“形”之间的关系,用数形结合的思想方法解决数学问题。
五、教学过程
(一)课前导入
师:同学们,你们认为数学是什么?
课件出示:数学是研究数量关系和空间形式的科学。
板书:数 与 形
师:今天我们就来研究数与形。大家看到这个题目,有什么问题吗?
预设:哪些数?什么图形?它们有什么关系/联系?(二)互动新授
1.数形互猜,初步感受
依次出示三个图形:
(1)
(2)
(3)
看到它们,你会想到哪个数?
小结:同学们,看到图形,我们能想到和它有关的数。看来数和形之间确实有关系。
2.数形结合,建立关联
师:接着看,你看到了什么?
(1)出示正方形数
问:发现规律了吗?如果按你发现的规律继续想,第四个图形是什么?和你想的一样吗?
追问:说明你发现的规律是对的,能用数或算式表达你发现的规律吗?写在纸上。
预设1:1,4,9,16
预设2:1×1,2×2,3×3,4×4
预设3:1,1+3,1+3+5,1+3+5+7(追问:谁读懂这个规律了?说到L型)
小结:同一组图形,尽管观察的角度不同,但都找到了“数的影子”。
(2)发现规律
1=1×1
1+3=2×2
1+3+5=3×3
1+3+5+7=4×4
为什么?1,2,3,4分别在哪里?
1,1+3,1+3+5,1+3+5+7是从1开始的连续奇数相加。
追问:能继续说吗?说的完吗?
有几个加数相加就是几的平方。
课件逐步出示:
小结:这么复杂的算式被这个简单的图形就表示了,说明数与形之间不仅有关系,还很紧密。
2.以形助数,深化联系
(1)出示:
1+3+5+7+9+11+13=( )
( ) =8^2
1+3+5+7+5+3+1=
追问:这个算式是怎么样的图形呢?
预设1:分成两半:1+3+5+7和1+3+5,4^2+3^2=25=5^2,5的平方怎么来的?
预设2:看成1+3+5+7+9
(2)3^2+4^2=5^2
视频解释以下公式。
(四)拓展贯通,感悟价值
过渡:其实,像这样借助数与形紧密关联的方法来解决问题的情况在我们小学阶段以往的数学学习中并不陌生。回想一下,在哪里见过?举例说明。
介绍:
(五)分层练习,回顾总结
1.出示:长方体沙坑,一辆载重 1.5 吨卡车。
你能提出什么数学问题?
出示:沙坑数据:长、宽、高分别是 2.5m、4m、1.5m。
汽车数据:长、宽、高分别是3m、7m、0.7m。
2.通过今天的学习,关于数与形,你们还有什么疑问吗?
