人教版(2019)必修第三册 9.2.2 库仑定律的应用 课件(共32张PPT)
文档属性
| 名称 | 人教版(2019)必修第三册 9.2.2 库仑定律的应用 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
9.2.2库仑定律的应用
1、内容:真空中两个点电荷之间相互作用的电力,跟它们的电荷量的乘积成正比,跟它们的距离的二次方成反比,作用力的方向在它们的连线上.
2、表达式:
3、适用条件:⑴ 真空 ⑵ 静止点电荷
k=9.0×109N·m2/C2
复习回顾
4、方向:在两点电荷的连线上,同种相斥,异种相吸。
5、静电力叠加原理:对于两以上的点电荷,其中每一个点电荷所受的总的静电力,等于其他点电荷分别单独存在时对该点电荷的作用力的矢量和。
丝线
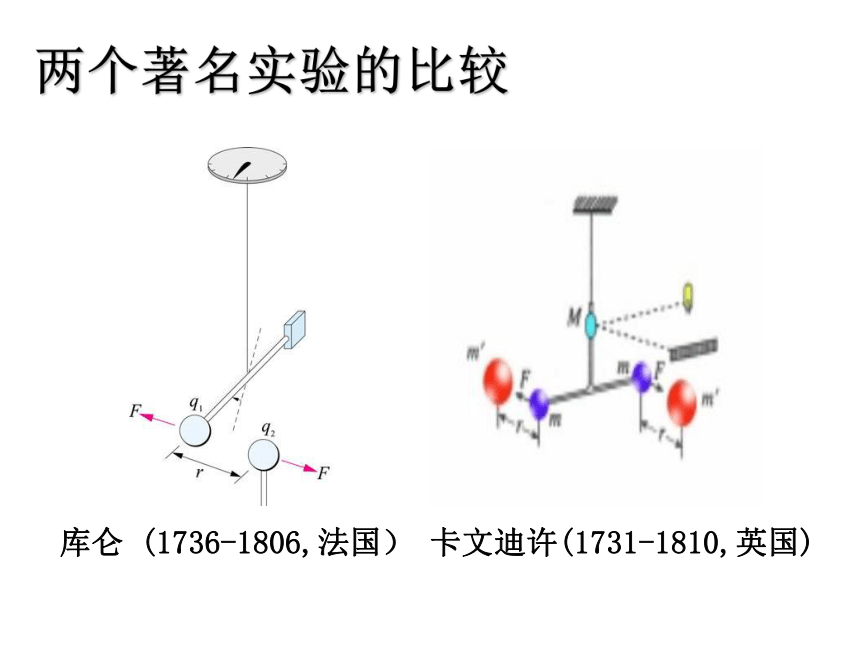
库仑 (1736-1806,法国) 卡文迪许(1731-1810,英国)
两个著名实验的比较
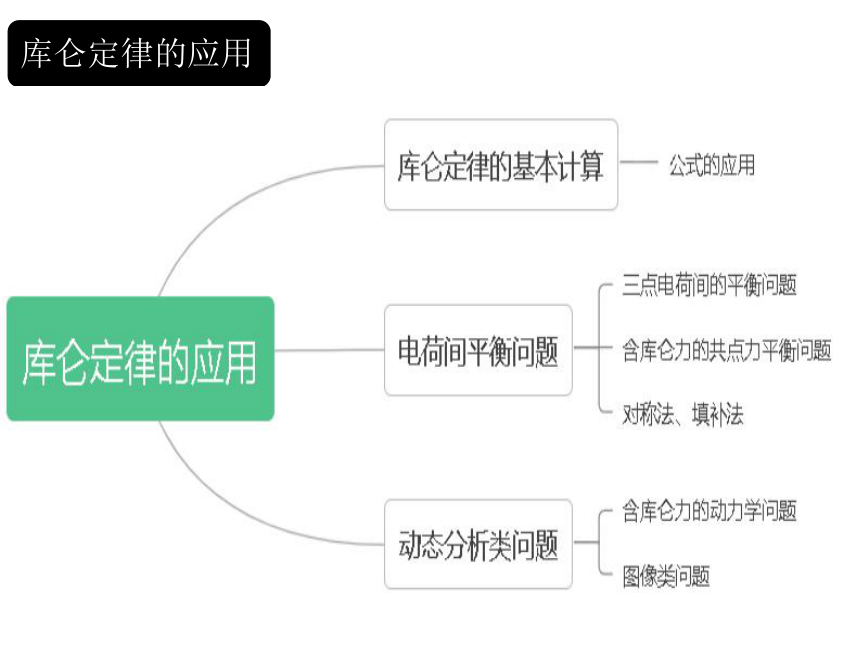
库仑定律的应用
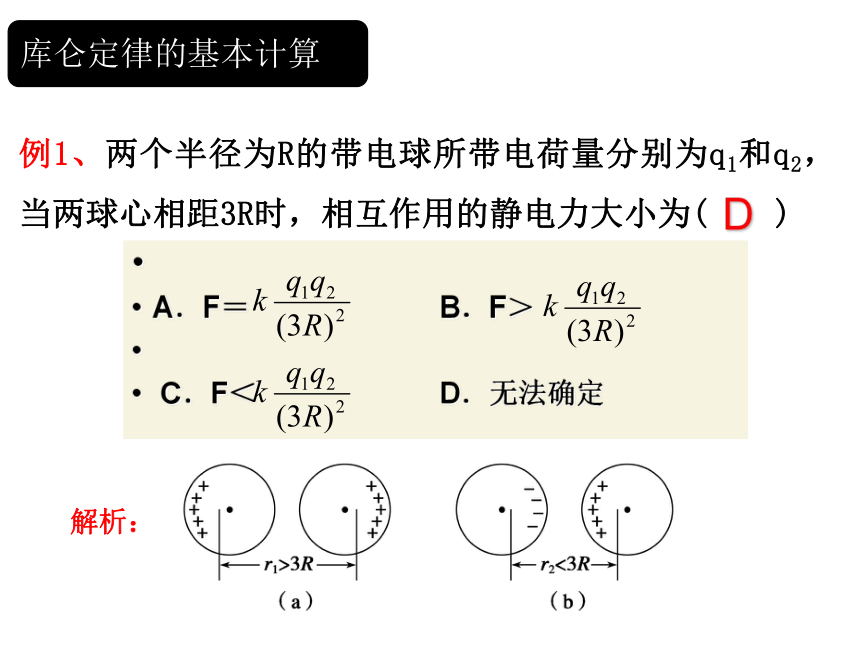
例1、两个半径为R的带电球所带电荷量分别为q1和q2,当两球心相距3R时,相互作用的静电力大小为( )
库仑定律的基本计算
D
A.F= B.F>
C.F< D.无法确定
解析:
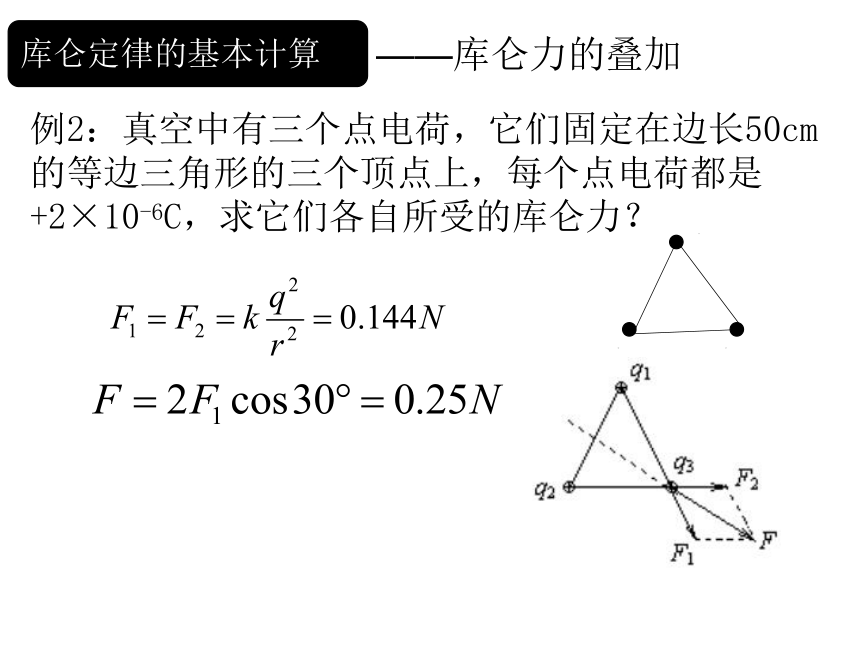
例2:真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们各自所受的库仑力?
q1
q2
q3
库仑定律的基本计算
——库仑力的叠加
变式1:真空中有三个带正电的点电荷,它们固定在腰长为100cm的等腰直角三角形的三个顶点上,每个点电荷的电荷量均为2.0×10-7C,求q3所受到的库仑力大小。(已知静电力常量k=9.0×109N·m2/C2,保留两位有效数字)
库仑定律的基本计算
答案:5.1×10-2N
——库仑力的叠加
库仑定律的基本计算
例3:真空中两个相同的金属小球A和B,A带电量为9Q,B带电量为-3Q,分别固定在两处,两球间静电力为F,用一个不带电的同样的金属小球C先和A接触,再与B接触,然后移去C,则AB球间的静电力应为多大?
若再使AB间距离增大一倍,则它们间的静电力又为多大?
F/8
F/32
电荷间的平衡问题
分析思路:
(1)确定对象
(2)受力分析
(3)矢量运算(合成、分解)
(4)运用平衡条件列方程
三点电荷的平衡问题
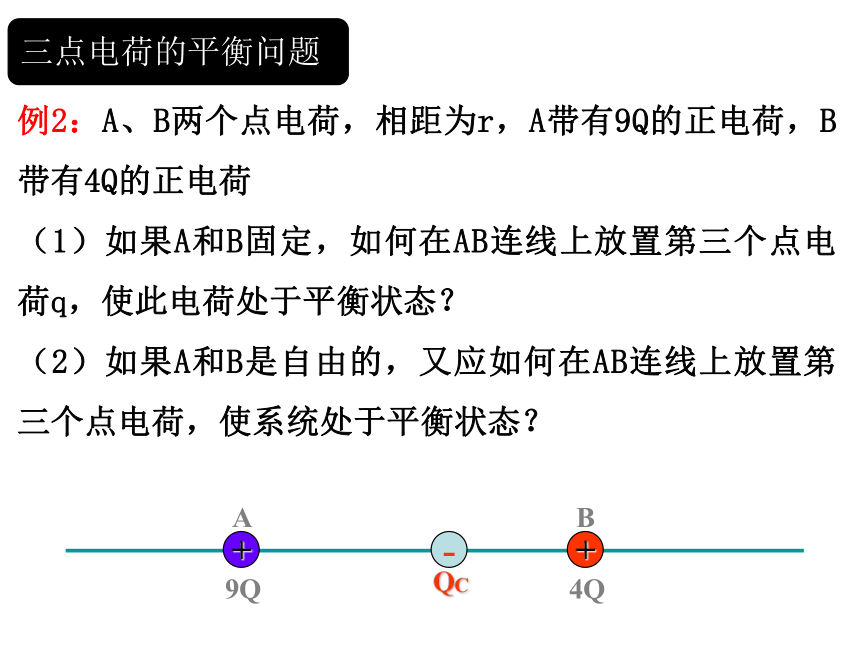
例2:A、B两个点电荷,相距为r,A带有9Q的正电荷,B带有4Q的正电荷
(1)如果A和B固定,如何在AB连线上放置第三个点电荷q,使此电荷处于平衡状态?
(2)如果A和B是自由的,又应如何在AB连线上放置第三个点电荷,使系统处于平衡状态?
+
+
A
B
9Q
4Q
-
QC
例3.一直线放三个可自由移动点电荷,若要它们均处于静止状态,试确定他们的电性与位置关系。
r1 r2
q1 q2 q3
q1 q2 q3
r1 r2
分析:
结论:
三点电荷的平衡问题
练习1.光滑绝缘的水平地面上有相距为L的点电荷A、B,带电量分别为-4Q和+Q,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
A -Q,在A左侧距A为L处
B -2Q,在A左侧距A为L/2处
C -4Q,在B右侧距B为L处
D + 2Q,在A右侧距A为3L/2处
L
-4Q Q
A B
C
例1:下列各图中A球系在绝缘细线的下端,B球固定在绝缘平面上,它们带电的种类以及位置已在图中标出.A球能保持静止的是( )
共点力的平衡问题
AD
例2:如图所示,在空间某处固定一带电小球A,,在A球正上方用一根长为L的绝缘细线把质量为m的小球B悬挂于此,稳定后发现小球A与小球B恰位于同一水平线上,已知细线与竖直方向成30°夹角,静电力常量为k,重力加速度大小为g,A、B均视为点电荷,求:
(1)A、B两球间的库仑力;
(2)若将A球下移,使得A、B两球间电库仑力恰好垂直与细线拉力,则此时的库仑力F1大小。
(3)当A球处于满足第(2)问的位置后,B球
从某时刻起开始漏电,以至于A、B两球间的
间距变为原来的一半,则此时的库仑力F2大小
与B球此时的带电量是原来的多少倍。
共点力的平衡问题
对称法、填补法解题
如图所示,半径为R的绝缘球壳上均匀带有电荷量为+Q的电荷,另一电荷量为+q的点电荷放在球心处,由于对称性,点电荷受力为零。现在球壳上挖去半径为r(r R)的一个小圆孔,则此时置于球心的点电荷所受静电力的大小为多少 方向如何 (已知静电力常量为k)
解析 解法一 由于球壳上均匀带电,原来每条直径两端相等的一小块面积上的电荷对球心处点电荷的静电力相互平衡。当在球壳上挖去半径为r的小圆孔后,因为是绝缘球壳,其余部分的电荷分布不改变,所以其他直径两端的电荷对球心处点电荷的作用力仍相互平衡,剩下的就是与小圆孔相对的半径也为r的一小块圆面上的电荷对它的作用力。又r R,所以这一带电小圆面可看成点电荷,库仑定律适用。小块圆面上的电荷量
【应用体验】
如图所示,一个半径为R的绝缘圆环均匀带电,ab为一极小的缺口,缺口长为L(L R),圆环所带电荷量为Q(正电荷),在圆心O处放置一所带电荷量为q的负点电荷,求负点电荷受到的库仑力的大小和方向。(已知静电力常量为k)
规律方法 对于不能视为点电荷的问题,可利用对称性、割补法等,化非点电荷为点电荷,这样可使难点得以突破,公式得以运用,问题可迎刃而解。
含库仑力的动力学问题
例1、如图所示,在绝缘的光滑水平面上,相隔一定距离有两个带同种电荷的小球,从静止同时释放,则两个小球的加速度和速度大小随时间变化的情况是( )
A.速度变大,加速度变大
B.速度变小,加速度变小
C.速度变大,加速度变小
D.速度变小,加速度变大
C
图像类问题
B
例2、如图,质量均为m的三个带电小球A、B、C,放置在光滑的绝缘水平面上,彼此相隔的距离为L(L比球半径r大的多),B球带电量为QB=-3q,A球带电量为QA=6q,若在C上加一水平向右的恒力F,要使A、B、C三球始终保持L的间距运动,求:C球所带电量和F的大小(已知静电力常量为k)
A
C
B
+
-
F
6q
-3q
QC
+
含库仑力的动力学问题
C球带正点还是负电?
答案:Qc=+8q F=18kq2/L2
含库仑力的动力学问题
例3、如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点的距离为l0释放后的乙球除受到甲球的静电力作用外,还受到一个大小为 为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.
(1)求乙球在释放瞬间的加速度大小;
(2)求乙球的速度最大时两球之间的距离;
(3)请定性地描述乙球在释放后的运动情况(说明速度的大小变化及运动方向的变化情况)
(2)当乙球所受的合力为零,即库仑力与恒力F大小相等时,乙球的加速度为零,速度最大,设此时两球之间的距离为x,则有: 解得:
解析:(1)由牛顿第二定律得: 解得:
(3)乙球先做远离甲球的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后就在B点和最远点之间做往复运动。
2.两个质量分别是m1、m2的小球,各用长为L的丝线悬挂在同一点,当两球分别带同种电荷,且电荷量分别为q1、q2时,两丝线张开一定的角度θ1、θ2,如图所示,则下列说法正确的是( )
A.若m1>m2,则θ1>θ2
B.若m1=m2,则θ1=θ2
C.若q1θ2
D.若q1=q2,则θ1=θ2
B
例2、如图2所示,A、B是两个带等量同种电荷的小球,A固定在竖直放置的10 cm长的绝缘支杆上,B 静止于光滑绝缘的倾角为30°的斜面上且恰与A 等高,若B的质量为30√3 g,则B带电荷量是多少?(取g=10 m/s2,小球A、B 视为点电荷, k=9×109N·m2/C2)
共点力的平衡问题
答案 1.0×10-6 C
课堂训练:
1.下列关于点电荷的说法正确的是( )
A.两个带电体无论多大,只要它们之间的距离远大于它们的大小,这两个带电体就可以看作点电荷
B.一个带电体只要它的体积很小,则在任何情况下,都可以看作点电荷
C.一个体积很大的带电体,在任何情况下,都不能看作点电荷
D.两个带电的金属小球,一定能将它们作为电荷集中在球心的点电荷处理
A
3.竖直墙面与水平地面均光滑且绝缘,小球A、B带同种电荷。现用水平向左推力F作用于小球B,两球分别静止在竖直墙和水平地面上,如图所示。如果将小球B向左推动少许,当两球重新达到平衡时,与原来的平衡状态相比较( )
A.推力F将变大
B.竖直墙面对小球A的弹力变大
C.地面对小球B的支持力不变
D.两小球之间的距离不变
C
4.如图所示,在绝缘水平面上固定三个带电小球a、b和c,相互之间的距离ab=4cm,bc=2cm,bc垂直于ac。已知小球b所受的库仑力的合力方向平行于ac边,设小球a和c的带电量的比值为k,则( )
A.a和c带同种电荷,k=4
B.a和c带异种电荷,k=4
C.a和c带同种电荷,k=8
D.a和c带异种电荷,k=8
D
5.在光滑绝缘的水平面上,有一个不导电的弹簧,两端各固定一个带电小球,两小球带有等量同种电荷,由于库仑力的作用弹簧伸长xo,如果将小球的电量都减少一半,则弹簧伸长是( )
A. xo /4 B. xo /2 C.大于 xo /4 D.小于 xo /4
6.如图,质量为m的三个带电小球放置在光滑的绝缘水平面上,彼此间距为L,带电量分别为qA=+10q、qB=-q,若在C球上加一个水平向右的恒力F,使得三球在运动过程中间距始终为L,则恒力F和C球带电量qC各是多少?
C
9.2.2库仑定律的应用
1、内容:真空中两个点电荷之间相互作用的电力,跟它们的电荷量的乘积成正比,跟它们的距离的二次方成反比,作用力的方向在它们的连线上.
2、表达式:
3、适用条件:⑴ 真空 ⑵ 静止点电荷
k=9.0×109N·m2/C2
复习回顾
4、方向:在两点电荷的连线上,同种相斥,异种相吸。
5、静电力叠加原理:对于两以上的点电荷,其中每一个点电荷所受的总的静电力,等于其他点电荷分别单独存在时对该点电荷的作用力的矢量和。
丝线
库仑 (1736-1806,法国) 卡文迪许(1731-1810,英国)
两个著名实验的比较
库仑定律的应用
例1、两个半径为R的带电球所带电荷量分别为q1和q2,当两球心相距3R时,相互作用的静电力大小为( )
库仑定律的基本计算
D
A.F= B.F>
C.F< D.无法确定
解析:
例2:真空中有三个点电荷,它们固定在边长50cm的等边三角形的三个顶点上,每个点电荷都是+2×10-6C,求它们各自所受的库仑力?
q1
q2
q3
库仑定律的基本计算
——库仑力的叠加
变式1:真空中有三个带正电的点电荷,它们固定在腰长为100cm的等腰直角三角形的三个顶点上,每个点电荷的电荷量均为2.0×10-7C,求q3所受到的库仑力大小。(已知静电力常量k=9.0×109N·m2/C2,保留两位有效数字)
库仑定律的基本计算
答案:5.1×10-2N
——库仑力的叠加
库仑定律的基本计算
例3:真空中两个相同的金属小球A和B,A带电量为9Q,B带电量为-3Q,分别固定在两处,两球间静电力为F,用一个不带电的同样的金属小球C先和A接触,再与B接触,然后移去C,则AB球间的静电力应为多大?
若再使AB间距离增大一倍,则它们间的静电力又为多大?
F/8
F/32
电荷间的平衡问题
分析思路:
(1)确定对象
(2)受力分析
(3)矢量运算(合成、分解)
(4)运用平衡条件列方程
三点电荷的平衡问题
例2:A、B两个点电荷,相距为r,A带有9Q的正电荷,B带有4Q的正电荷
(1)如果A和B固定,如何在AB连线上放置第三个点电荷q,使此电荷处于平衡状态?
(2)如果A和B是自由的,又应如何在AB连线上放置第三个点电荷,使系统处于平衡状态?
+
+
A
B
9Q
4Q
-
QC
例3.一直线放三个可自由移动点电荷,若要它们均处于静止状态,试确定他们的电性与位置关系。
r1 r2
q1 q2 q3
q1 q2 q3
r1 r2
分析:
结论:
三点电荷的平衡问题
练习1.光滑绝缘的水平地面上有相距为L的点电荷A、B,带电量分别为-4Q和+Q,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
A -Q,在A左侧距A为L处
B -2Q,在A左侧距A为L/2处
C -4Q,在B右侧距B为L处
D + 2Q,在A右侧距A为3L/2处
L
-4Q Q
A B
C
例1:下列各图中A球系在绝缘细线的下端,B球固定在绝缘平面上,它们带电的种类以及位置已在图中标出.A球能保持静止的是( )
共点力的平衡问题
AD
例2:如图所示,在空间某处固定一带电小球A,,在A球正上方用一根长为L的绝缘细线把质量为m的小球B悬挂于此,稳定后发现小球A与小球B恰位于同一水平线上,已知细线与竖直方向成30°夹角,静电力常量为k,重力加速度大小为g,A、B均视为点电荷,求:
(1)A、B两球间的库仑力;
(2)若将A球下移,使得A、B两球间电库仑力恰好垂直与细线拉力,则此时的库仑力F1大小。
(3)当A球处于满足第(2)问的位置后,B球
从某时刻起开始漏电,以至于A、B两球间的
间距变为原来的一半,则此时的库仑力F2大小
与B球此时的带电量是原来的多少倍。
共点力的平衡问题
对称法、填补法解题
如图所示,半径为R的绝缘球壳上均匀带有电荷量为+Q的电荷,另一电荷量为+q的点电荷放在球心处,由于对称性,点电荷受力为零。现在球壳上挖去半径为r(r R)的一个小圆孔,则此时置于球心的点电荷所受静电力的大小为多少 方向如何 (已知静电力常量为k)
解析 解法一 由于球壳上均匀带电,原来每条直径两端相等的一小块面积上的电荷对球心处点电荷的静电力相互平衡。当在球壳上挖去半径为r的小圆孔后,因为是绝缘球壳,其余部分的电荷分布不改变,所以其他直径两端的电荷对球心处点电荷的作用力仍相互平衡,剩下的就是与小圆孔相对的半径也为r的一小块圆面上的电荷对它的作用力。又r R,所以这一带电小圆面可看成点电荷,库仑定律适用。小块圆面上的电荷量
【应用体验】
如图所示,一个半径为R的绝缘圆环均匀带电,ab为一极小的缺口,缺口长为L(L R),圆环所带电荷量为Q(正电荷),在圆心O处放置一所带电荷量为q的负点电荷,求负点电荷受到的库仑力的大小和方向。(已知静电力常量为k)
规律方法 对于不能视为点电荷的问题,可利用对称性、割补法等,化非点电荷为点电荷,这样可使难点得以突破,公式得以运用,问题可迎刃而解。
含库仑力的动力学问题
例1、如图所示,在绝缘的光滑水平面上,相隔一定距离有两个带同种电荷的小球,从静止同时释放,则两个小球的加速度和速度大小随时间变化的情况是( )
A.速度变大,加速度变大
B.速度变小,加速度变小
C.速度变大,加速度变小
D.速度变小,加速度变大
C
图像类问题
B
例2、如图,质量均为m的三个带电小球A、B、C,放置在光滑的绝缘水平面上,彼此相隔的距离为L(L比球半径r大的多),B球带电量为QB=-3q,A球带电量为QA=6q,若在C上加一水平向右的恒力F,要使A、B、C三球始终保持L的间距运动,求:C球所带电量和F的大小(已知静电力常量为k)
A
C
B
+
-
F
6q
-3q
QC
+
含库仑力的动力学问题
C球带正点还是负电?
答案:Qc=+8q F=18kq2/L2
含库仑力的动力学问题
例3、如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电荷量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电荷量为q;A、B两点的距离为l0释放后的乙球除受到甲球的静电力作用外,还受到一个大小为 为静电力常量)、方向指向甲球的恒力作用,两球均可视为点电荷.
(1)求乙球在释放瞬间的加速度大小;
(2)求乙球的速度最大时两球之间的距离;
(3)请定性地描述乙球在释放后的运动情况(说明速度的大小变化及运动方向的变化情况)
(2)当乙球所受的合力为零,即库仑力与恒力F大小相等时,乙球的加速度为零,速度最大,设此时两球之间的距离为x,则有: 解得:
解析:(1)由牛顿第二定律得: 解得:
(3)乙球先做远离甲球的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后就在B点和最远点之间做往复运动。
2.两个质量分别是m1、m2的小球,各用长为L的丝线悬挂在同一点,当两球分别带同种电荷,且电荷量分别为q1、q2时,两丝线张开一定的角度θ1、θ2,如图所示,则下列说法正确的是( )
A.若m1>m2,则θ1>θ2
B.若m1=m2,则θ1=θ2
C.若q1
D.若q1=q2,则θ1=θ2
B
例2、如图2所示,A、B是两个带等量同种电荷的小球,A固定在竖直放置的10 cm长的绝缘支杆上,B 静止于光滑绝缘的倾角为30°的斜面上且恰与A 等高,若B的质量为30√3 g,则B带电荷量是多少?(取g=10 m/s2,小球A、B 视为点电荷, k=9×109N·m2/C2)
共点力的平衡问题
答案 1.0×10-6 C
课堂训练:
1.下列关于点电荷的说法正确的是( )
A.两个带电体无论多大,只要它们之间的距离远大于它们的大小,这两个带电体就可以看作点电荷
B.一个带电体只要它的体积很小,则在任何情况下,都可以看作点电荷
C.一个体积很大的带电体,在任何情况下,都不能看作点电荷
D.两个带电的金属小球,一定能将它们作为电荷集中在球心的点电荷处理
A
3.竖直墙面与水平地面均光滑且绝缘,小球A、B带同种电荷。现用水平向左推力F作用于小球B,两球分别静止在竖直墙和水平地面上,如图所示。如果将小球B向左推动少许,当两球重新达到平衡时,与原来的平衡状态相比较( )
A.推力F将变大
B.竖直墙面对小球A的弹力变大
C.地面对小球B的支持力不变
D.两小球之间的距离不变
C
4.如图所示,在绝缘水平面上固定三个带电小球a、b和c,相互之间的距离ab=4cm,bc=2cm,bc垂直于ac。已知小球b所受的库仑力的合力方向平行于ac边,设小球a和c的带电量的比值为k,则( )
A.a和c带同种电荷,k=4
B.a和c带异种电荷,k=4
C.a和c带同种电荷,k=8
D.a和c带异种电荷,k=8
D
5.在光滑绝缘的水平面上,有一个不导电的弹簧,两端各固定一个带电小球,两小球带有等量同种电荷,由于库仑力的作用弹簧伸长xo,如果将小球的电量都减少一半,则弹簧伸长是( )
A. xo /4 B. xo /2 C.大于 xo /4 D.小于 xo /4
6.如图,质量为m的三个带电小球放置在光滑的绝缘水平面上,彼此间距为L,带电量分别为qA=+10q、qB=-q,若在C球上加一个水平向右的恒力F,使得三球在运动过程中间距始终为L,则恒力F和C球带电量qC各是多少?
C
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
